
3つの質問をして、似ている傾向の人をグルーピングする方法
非常勤講師を務めている大学で、学生をグルーピングする際に用いた方法をメモしておく。(今回はGoogleフォームと、その結果を書きだしたGoogleスプレッドシートを用いたやり方です。「MATLAB」などのデータ分析専用アプリがあればもっと複雑なことも簡単にできると思います。お金がある人はそっちを使いこなした方がよいでしょう。)
さて、授業の中で学生にグループ制作をしてもらうことは色々意義深いのでぜひともやったら良いとは思うのだが、実際にグループを分けるとなると、その方法はなかなか一筋縄にはいかない。単に仲良しグループが同じになれば良いのか?というと各々が持っているスキルセットも異なるし、かといって趣向もまったくばらけていたらシナジーが働かないことだってある。学生にとっても何らかのかたちで納得性の高い、合理的な方法はないだろうか?ということをゴニョゴニョ考えていた。
そこでこのたび、表題にあるように「3つの質問をして似ている傾向の人をグルーピングしてみる」というやり方を試してみた。具体的な手順は以下の4ステップ。
(1)Googleフォームで、氏名と、数値で答えられる3つの質問(1-10という数値による回答)を設定して回答を貰う。例えば何らかの制作物をグループで作るとなった時に「おバカを1、知的を10とした場合、目指すネタの方向を数値で回答してください」とか。おバカなネタをやりたい場合は1、知的なネタをやりたい場合は10、中間なら4-6あたり、といった具合で回答してもらう。(今回、そんな質問はしていないけど、1〜10など数値で答えられる質問を前提に考えてみた)
(2)フォームの回答からスプレッドシートを生成し、名前+3項目の表が作られる(下の表)。
(3)回答は3次元空間として表わされていることになるので、任意の二点間の距離を計算することで、各々の距離として近いものを調べる。
(4)結果としてでた値を、近いものをグルーピングする、など具体的に応用する。

上記の例では、Q1〜Q3の3つの質問をしてその回答を表示している。回答した順に並んでいるのだが、一番早く答えた学生1や学生2は極端な傾向の回答をしているし、学生14から学生16あたりはとても中庸な傾向を持つ(回答の素早さと極端さはまた関係がありそうで面白いけど、今回はそこは触れない)。極端な回答と中庸な回答を3次元空間にプロットした場合、学生1は、座標の端っこに位置し、学生16は座標の中央辺りにいる、ということになる。
次に、これらの回答を順次比較していく。学生1が、学生2以降の他の学生とどのような距離があるか?を考えていく。これは3次元空間の座標におけるAB間の距離の公式
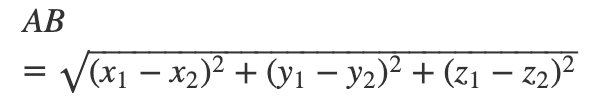
より求めることができる。これをスプレッドシートの関数として書いていく。例えば上記表でいうと、学生1の回答がセルB2, C2, D2にあり、学生2の回答がセルB3, C3, D3に記入されている。これをスプレッドシートの関数として計算させるためには以下のようになる。
=SQRT(((B2-B3)^2)+((C2-C3)^2)+((D2-D3)^2))
「SQRT」という関数は、平方根という意味。「^2」は、2乗という意味。小数点以下はあまり多くても意味無いので、今回は小数点2位まで表示した。学生1から学生18までそれぞれの距離を計算した結果がこちら。

表の見方としては、縦と横の学生名の交点にその2人の距離が表示されている。上の表では何となく近い人どうしを見やすくするために計算結果の距離が2.99以下の値にはグリーンの色が付くように「条件付き書式」を設定している。
やってみて面白かったポイントは3つ。まず1つ目に、質問は3つだが、一つは傾向の異なる質問にしておくと面白い。たとえば「学校に行く理由」を3つ設定するならば、「Q1 学問を深く理解するため」「Q2 問題を早く解けるようになるため」に加えて「Q3 友達と会うのが楽しいから」という毛色の異なる質問を入れておく。また必要であればここの質問の重みづけも変えられる。「Q3 面白いから」という項目の回答を「×2」してやれば、Q1、Q2に対して、Q3の影響力を大きくすることもできる。(少なくとも僕は勉強するために学校に行っていたという記憶はない)
2つ目に、二点間の距離を計算する数式はオートフィル機能ですぐに作れないので、素早く結果が必要なワークショップや授業中に用いる場合は、事前に計算式を入力したセルを準備しておくとよい。(今回は手作業で20分ぐらい掛かってしまい学生を待たせてしまった。もしかしたらちゃんと調べれば、オートフィルで簡単に作れる方法があるのかもしれないけど、そのあたりはエクセルに詳しい人、教えてください)
3つ目に、グルーピングする時には最も特異な人からグルーピングしてくほうが決まりやすいんじゃないか?という気がした。3次元座標の中央辺りからまとめていくと、最後に端に居る人があぶれてしまうかもしれないので、むしろ極端な人の方からしらべて、その人に近いひとをまとめていくと良さそうと思った。上記事例だと、学生1が極端な傾向があったので、学生1と比較的近い学生5(距離8.06)と、学生11、12(それぞれ距離8.31)を一つのグループとした。また、学生2についても比較的他の学生と離れている=極端な傾向を持つのだが、学生2の方から近い順に選ぶと、学生9、16が、距離3.16という値、次に近いのが、学生17、18、距離3.32という値だったが、ただしこれを基準にグループ化してしまうと、学生18にとっては、もっと近い学生14(距離1.41)とか、学生3(距離2.00)などと組めなくなってしまう。そうしたことも諸々考慮して、結局学生2は、学生9、16(それぞれ距離3.16)と、学生8(距離4.36)と組んでもらうことにした。近い同士を結びつけるといっても、遠く離れた人を孤立化させる訳にも行かないので、たとえば学生11から見てみると2.00とか2.24など近い学生が他にもいるにも関わらず、学生1からみて近いという理由で、学生1と同じグループになっている。それでも今回はグループワーク用のチーム作りのためにこの結果を用いているので、こうしたグルーピングになったが、離れたものは孤立化させても構わないようなグループ分けをする場合はまた違ったグルーピングになるはずである。要素同士の距離が出たということと、その距離をどのように応用するかというのは別問題なので、混同しないように気をつけたい。
この時は結果として、18人の学生を、3-4人のグループ5つに分けた。どのグループを3人にするのか、また4人にするのか?とか、学生1のように極端な場所に居る人をどう扱うかといった問題は上記に述べたように単一的な解答がないのでここでは考えないが、とにかくある程度の学生をこのように似たような傾向で括ってグループにするという方法は、結果として概ね学生本人たちにも納得感が高かったようだ。

実際に配置を3Dで表したのが上図。3D散布図などと呼ばれるグラフだが、エクセルとかGoogleスプレッドシートとかでは2D散布図までしか描けないので、今回はSketchUpで手作業で配置してみた。7と6は結果が同じだったので視認性のために少しだけずらして配置してある。オレンジ色の17と、ミドリ色の8は入れ替えても良かったかも知れないが、ある程度のランダム性も残す意味でもこのままとした。
人間は複雑な事象を直感的に理解するのが苦手で、そのため2つぐらいまで絞り込んだ指標を用いて理解しようとする。これがいわゆるKPIというもの。平面座標系は直感的に理解しやすいのでX,Y軸の2次元プロットを良く用いる。分かりやすいのは横軸に時間をプロットした表である。売上を縦軸、年度を横軸にプロットすれば良く売れているのか、売上が減ってきているのかといった傾向を把握するのが容易になる。
ただし、3つの軸があるような問題、たとえば事業所ごとの「利益額」「社員満足度」「残業時間」といったものをまとめて考え始めると途端に直感が働かなくなってしまう。3軸評価した上で、似ているもの同士をまとめることができると、各事業その特徴や傾向などを分析するのに役立つかもしれない。そうした場合今回のように、3軸上の距離を測る仕組みを用意しておけば役に立つ可能性がでてくる。仲良しと組みたかった、などの意見はあるだろうがそうしたこととは別に、グループとして目指す方向についてはある程度傾向が似ていたので、スムースに話し合いが進み出した、という意味で上手くいった。
さて、なぜ3軸評価なのか?ということを少し述べてみたいと思う。ミュージアムエデュケーターとしてワークショップを数多くデザインしたりファシリテーションしたりするが、よくある質問として「ワークショップの評価はどうやるの?」というものがある。特に教育を専門にしている人にとってはワークショップのように成果が測りにくいものをどう取り扱って良いのか困る、ということは想像に難くない。この質問についてずっと考えていて至ったのが「第3の軸」という考え方であった。先の事例でいうと学校の価値を測るのには「深く理解する」「早く解ける」というのがX,Y軸にあるはずで、これを極めていくとたとえば東京大学の入学が叶う、ということになる。ただし、すべての学生が東大を目指して学校に行くのか?というとそうとも限らなくて、単に「楽しいから学校に行く」ということもあるだろう。こうした3つ目のZ軸というのは大切な意味があるように思われた。貧困にあえぐ地域では場合によってはZ軸に「給食が食べられるから行く」という理由も設定できるかも知れない。実はワークショップの評価軸ということを考えるならば、従来の教育の評価方法とは異なるやり方を考える必要があるのではないか?と思うようになった。実際にワークショップのデザインをしてファシリテーションを行う中で、手応えを感じるのは、事前に用意されていたX,Yの価値軸とは別に、参加者の中から新たな評価軸Zが発見された時だと言える。もしそうなのだとしたら、参加者が新たな価値軸を作った上で参加者同士その軸上に成果をプロットし始めて、何かしらの新しい発見をする、という活動にまで展開していくことを測ることで、価値あるワークショップを見いだすことができるのかもしれない。
そんなことを考きた中で、今回のように3次元の評価を応用する方法として、2点間の距離から似た者同士を探す、というやり方を思いついた次第だ。今後、自分でもワークショップなどのグループ分けをする時に、こうした手法を使って似た傾向の人をまとめる手法を応用してみて、使い物になるかどうかを引き続き検証してみようと思う。また、この手法は他にも応用が利きそうなので引き続き考えてみたいと思う。
