ベイズ統計学で制約条件を特定してみたい
※この記事はなんとなくの思いつきで適当に書いていますのでご注意ください(予防線)
マーケティングとイノベーションの定義
ドラッカーによれば、会社には2つの基本的な機能があるようです。マーケティングとイノベーションです。
でもマーケティングとイノベーションと言われても、なんかわかるようでわからないですよね。そこで僕はこのように定義しています。
マーケティングとは"伝わるように伝えること"
イノベーションとは"変わるように変えること"
マーケティングは相手に情報を伝えるだけではダメで、伝えた情報が相手に伝わって初めて効果があったと言えます。そして、イノベーションは何かを変えるだけではダメで、何かを変えたことで会社の重要な数字などが変わることで初めて効果があったと言えます。
つまり、会社の利益を向上させるためには、"利益が変わるように変える"ようなイノベーションを行うことが大切だということです。もちろん、会社の重要な数字というのは、経営哲学やKGI/KPIなどによって変わってきます。
イノベーションを起こすために答えるべき3つの質問
さて、このような変化を起こすことのできる、好いイノベーションを行うためには、以下の3つの質問に適切に答える必要があると考えます。
3つの質問とは以下の3つです。
(利益を変えるために)なにを変えるか?
(利益を変えるために)なにに変えるか?
(利益を変えるために)どうやって変えるか?
この3つの質問は、エリヤフ・ゴールドラット博士著の『ザ・ゴール』に書かれていた、"マネージャーが答える必要のある質問"から来ています。とても汎用性が高く、様々な場面で使える質問です。
さて、この記事では最初の2つの質問、”なにを変えるか?”と"なにに変えるか?"に答えるために、TOC(制約条件の理論:Theory of Constraints)を活用することを考えてみます。
TOC(制約条件の理論:Theory of Constraints)の活用
まずは最初の質問について考えてみましょう。
会社の利益を増やすために、なにを変える必要があるか?
TOCの重要な考え方の1つに、"局所最適化が全体最適化につながるとは限らない"というものがあります。つまり、プロセスの一部を頑張って変えたとしても、それが全体の利益に繋がるとは限らないということです。
では、なにを変えることが全体最適化につながるのでしょうか?TOCでは、スループット(=組織が創り出している価値)は、その組織の中の一番弱い部分によって上限が制限されていると考えます。
この一番弱い部分を"制約条件"と呼びます。
つまり、"なにを変えるか?"という質問の答えは、"自分の組織の制約条件はなにか?"という質問に答えることと、ほとんど一緒だということになります。実にシンプルですよね。
では、制約条件はどのように見つけたらいいのでしょうか?
製造工程の場合、現場を見ればわかることが多いです。なぜなら制約条件の前には仕掛かり中の在庫が積み上がっているはずだからです。業務プロセスの場合、業務や仕事が溜まっている場所が制約条件の可能性が高いでしょう。
なぜなら制約条件を考慮せずにプロセスを動かしている場合、一番処理が遅い場所になるのが制約条件だからです。
では、業務や在庫が溜まっている場所がない場合はどうなるのでしょうか?
その場合は、社内に制約条件はなく、市場が制約条件になっている可能性があります。つまり、生産やサービスはもっと多くの需要に対応できるのに、売ることのできる数が少ないため、そこまで頑張って生産しなくても大丈夫、という状況になります。
このようにある程度は勘や経験で制約条件を見つけることができるかもしれませんが、一番好いのはデータから制約条件を見つけ出すことができることです。
プロセス全体のフロー図の作成
まずはTOCの生まれた背景を鑑みて、シンプルな生産工程を考えてみましょう。もちろん生産以外の業務にも応用可能な内容となっています。
最初に行うべきことは、対象となるプロセスの全体像を把握することです。プロセスの全体像がわからなければ、局所最適化が全体最適につながるかどうかがわからなくなってしまいます。
どの範囲を"全体"とするかはあなたの"影響の輪"によるでしょう。スティーブン・R・コヴィー著の『7つの習慣』によれば、"影響の輪"はあなた自身が変えたり影響を与えたりできる範囲のことです。
一般的な企業であれば、役職が高ければ高いほど、この範囲は広くなることでしょう。
次に、このプロセスを細かい作業に分解していく必要があります。
リーン/TPS(トヨタ生産方式)におけるバリューストリームマップ(VSM)やビジネスプロセス・マネジメントのプロセスマップなどを作るのも好いでしょう。
方法は何でも好いのですが、プロセスを一覧にして簡単に見れる状態にしておくことが重要です。
まずは、簡単な例を見てみましょう。

この図はRのDiagrammeRというパッケージを使って作成しています。RStudioでフローチャートなどを作りたい時に便利です。詳しい説明は今回は行いませんので、興味のある方は公式サイトを見てみてください。
Rコード
DiagrammeR::grViz("TOC_simple.dot")ファイル:TOC_simple.dot
digraph test_graph{
graph[rankdir = TD,
label ="TOC_simple",
labelloc = t
fontsize = 10,
fontcolor = black,
bgcolor = Khaki,
nodesep = 0.5,
ranksep = 0.5]
node[style="filled",shape=rect,color=green]
<材料\n2000円/個>
node[style="filled",shape=rect,color=DeepSkyBlue]
<工程A\n15分/個>
<工程B\n10分/個>
<工程C\n12分/個>
node[style="filled",shape=rect,color=LightCoral]
<材料\n2000円/個> -> <工程A\n15分/個> -> <工程B\n10分/個> -> <工程C\n12分/個> -> <製品\n販売価格8000円/個\n販売可能数:100個/週>
{rank = same; <材料\n2000円/個>; <工程A\n15分/個>; <工程B\n10分/個>; <工程C\n12分/個>; <製品\n販売価格8000円/個\n販売可能数:100個/週>;}
}プロセスの全体像の説明

シンプルな生産工程のフロー図
というわけで非常に簡単なプロセスを書いてみました。シンプルすぎて、どこが制約なのかすぐにわかってしまいそうですが、それはそれで後で実行するプログラムが正しく動いているか確かめやすくなります。
さて、このプロセスでは材料を1つ使い、3つの異なる生産工程を経て、製品へと生まれ変わります。材料費は2,000円かかりますが、この材料はいつでも自由に同じ値段で仕入れることができると仮定しましょう。
各生産工程では、記載されている作業時間がかかることになります。それぞれ別の社員が担当しており、作業時間は独立しています。また、各社員は1日8時間働くことができて、残業はできないこととします。
それらの生産工程を通り抜けたら、最終的に8,000円で市場に売ることができるようになります。このとき、製品は市場で毎週確実に100個売ることができることとします。
では、このプロセスにおいて制約条件はどこにあるでしょうか?
プロセスの制約条件を手計算する
まず、材料の仕入れに関しては、いつでも自由にできることになっているので制約条件にはなり得ません。
次に各生産工程が毎週最大いくつの製品を作ることができるかをみてみましょう。
各社員は1日に8時間働くことができるので、8時間×60分で480分。週5日なので480分×5日で2400分の作業を行うことができます。この作業時間を1個当たりの作業時間で割れば、最大生産数を求めることができます。
工程A:2400分/15分 = 160個
工程B:2400分/10分 = 240個
工程C:2400分/12分 = 200個
簡単ですね。
ただし、これだけの数の製品を作ったとしても、市場では毎週100個しか売ることができません。
つまり、このプロセスの場合、制約条件は市場にあることになります。100個×8,000円で80万円の売上を得ることができます。
ここで重要なことは、もし市場の制約をすぐに伸ばすことができないのであれば、各生産工程でそれ以上の数を作れたとしても、作らないという判断が必要になるということです。
市場で100個までしか売れないのであれば、100個しかつくらない。これがJIT/TPSなどで言われる"必要な分だけ作る"ということにつながります。TOCにおいては、制約条件に従属するというステップにも関係してきます。
100個生産することにした場合、材料費が2,000円×100個で20万円かかります。つまり、このプロセスでの最終的な利益は60万円ということになります。
実際にはここから作業者の業務費用などが引かれることになりますが、今回は簡単にするため考えません。
プロセスの制約条件をプログラミングで解く(PuLP)
今回プロセスが簡単でしたので、すぐに計算して制約条件を求めることができました。…でも、これをいちいち計算するのは面倒ですよね。もっと早く簡単に制約条件を見つけることはできないでしょうか。
せっかくなのでプログラムを書いて、この問題を解いてもらうようにしましょう。
こうした問題を解くために使える便利なツールが、"線形計画法"(LP:Linear Programming)です。
線形計画法とは、簡単に説明すると、ある制限の下で、指定された式の結果を最大(もしくは最小)になるように解いてくれるものです。
この線形計画法はPythonを利用して実行することができます。使うライブラリはPuLPです。まずは、このプロセスの制約条件を見つけることのできる実装例を見てみましょう。

シンプルな生産工程のフロー図
Pythonコード
import pulp
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=100) #最大販売数量100個
A = pulp.LpVariable('A', cat="Integer",lowBound=0,upBound=2400) #最大作業時間2400分
B = pulp.LpVariable('B', cat="Integer",lowBound=0,upBound=2400)
C = pulp.LpVariable('C', cat="Integer",lowBound=0,upBound=2400)
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P #販売価格 - 材料費
revenue += 15*P == A # 各作業者の作業時間の制約
revenue += 10*P == B
revenue += 12*P == C
revenue.solve()
print(pulp.value(P))
print(pulp.value(A), pulp.value(B),pulp.value(C))
print("Revenue = ", pulp.value(revenue.objective))実行結果
100.0
1500.0 1000.0 1200.0
Revenue = 600000.0コードの解説をしていきます。
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=100) #最大販売数量100個
A = pulp.LpVariable('A', cat="Integer",lowBound=0,upBound=2400) #最大作業時間2400分
B = pulp.LpVariable('B', cat="Integer",lowBound=0,upBound=2400)
C = pulp.LpVariable('C', cat="Integer",lowBound=0,upBound=2400)まず最初に変数を作成します。これらの変数は線形計画法を解くために使われる値になります。
Pは製品Pの変数となっており、販売可能な製品の数を表します。lowBoundで販売数の下限を設定し、upBoundで最大数を設定しています。例えば、他の変数に制約条件があった場合、100個売る能力があるのに売れない状態になるため、0~100個のあいだの数が販売数になることになります。
A,B,Cは各生産工程の作業時間を表しています。最大で2400分働くことができるので、0~2400分のあいだの数の時間分働くことになります。
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解くrevenueを定義している最初のコードは、PuLPでどんな問題を解くかを指定しています。今回の場合はpulp.LpMaximizeに設定しているため、最大化問題を解くことになります。どんな式を最大化するかは、次の行で設定しています。
revenue += (8000-2000)*P # 販売価格 - 材料費 今回の線形計画法ではこの式を最大化します。Pを1個販売するごとに8,000円の売上があがり、1個につき材料費2,000円がかかります。
revenue += 15*P == A # 各作業者の作業時間の制約
revenue += 10*P == B
revenue += 12*P == C次の3行は各生産工程A,B,Cの制約条件を表しています。製品Pを1個製造するごとに各工程の作業時間がかかるので、工程の作業時間×Pの値がそれぞれの変数の値になるようにしています。
つまり、Pが10だった場合、Aは15*10=150となるという具合です。Aの最大値は2400分という制約があるため、際限なく製造することはできないということになります。
revenue.solve()
もしくは
revenue.solve(pulp.PULP_CBC_CMD(msg=0)) 最後に、この問題を解くように指示を出します。このとき、pulp.PULP_CBC_CMD(msg=0)を指定すると、ログが出ないようになります。
さて、このコードを実行し、結果を表示すると以下のようになりました。
最大化問題を解いた後、各変数がどのような値になっているかを確認するには、pulp.value(変数名)で表示できます。最大化された式の値はpulp.value(revenue.objective))で取得できます。
print(pulp.value(P))
>>> 100.0print(pulp.value(A), pulp.value(B),pulp.value(C))
>>> 1500.0 1000.0 1200.0print("Revenue = ", pulp.value(revenue.objective))
>>> Revenue = 600000.0週の販売数はP=100個。Aの作業時間は1500分、Bの作業時間は1000分、Cの作業時間は1200分となりました。最終的な利益は60万円で、手で計算した通りの結果になっています。
ここでA,B,Cは作業時間を全て使っておらず、制約条件ではないことがわかります。最大値となっているのはPなのでPが制約条件ということも分かりますね。
複雑なプロセスの制約条件をPuLPで解く
では次はこのプロセスを少し複雑にしてみましょう。
現時点で各生産工程の作業時間が余っていることがわかったので、新しい製品Sを作ることにしました。製品Sは作業時間は多くかかりますが、製品Pの倍の値段で売ることができます。
このプロセスを図にすると以下のようになりました。

製品が2つになっただけで計算が複雑になったのではないでしょうか。
制約条件を手計算する
まずは手計算してみましょう。まずは社内に制約がないと考えて、製品Sと製品Pの販売可能数をすべて製造してみます。
するとA,B,Cの各工程の作業時間は以下のようになります。
工程A:22分*50個+15分*100個=2600分
工程B:30分*50個+10分*100個 =2500分
工程C:24分*50個+12分*100個=2400分
最大作業時間は2400分なので、どうやらAとBの作業時間が足りないことがわかります。生産する時間が足りないので、製品Pか製品Sのいくつかを生産することを諦めなければなりません。
では、製品Sと製品Pのどちらを減らすべきでしょうか?
まず一番作業時間の多い、Aの作業時間を減らすことを考えてみましょう。もしAが制約条件であるならば、Aの作業時間を最も効果的に使わなければなりません。つまり、Aの作業時間あたりの売上を計算する必要があります。
これを計算すると以下のようになります。
製品Pを作った場合、8,000円/15分=533.3円/分
製品Sを作った場合、16,000円/22分=727円/分
つまり、工程Aにとっては、製品Sを作った方が1分あたりの価値が高いことがわかります。これをTOCではスループット・ダラーと呼んでいます。
それでは、生産する製品Pの数を減らして、工程Aが2400分に収まるようにしましょう。現時点から200分減らす必要があります。製品Pの数を14個減らす必要があります。
このとき、工程Bの作業時間も製品Pの14個分減ることになります。つまり、工程Bの作業時間は2360分となり、制約条件ではなくなります。
つまり、このプロセスで得られる最大の週間利益は、製品Sを50個、製品Pを86個生産することで得られることになります。
(16000円-4000円)*50個+(8000円-2000円)*86個
= 60万円+ 51万6千円 = 111万6千円
線形計画法で計算した場合、どうなるかみてみましょう。
PuLPで計算
import pulp
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=100) #最大販売数量100個
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=50) #最大販売数量50個
A = pulp.LpVariable('A', cat="Integer",lowBound=0,upBound=2400) #最大作業時間2400分
B = pulp.LpVariable('B', cat="Integer",lowBound=0,upBound=2400)
C = pulp.LpVariable('C', cat="Integer",lowBound=0,upBound=2400)
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P + (16000-4000)*S #販売価格 - 材料費
revenue += 15*P + 22*S == A # 各作業者の作業時間の制約
revenue += 10*P + 30*S == B
revenue += 12*P + 24*S == C
revenue.solve()
print(pulp.value(P),pulp.value(S))
print(pulp.value(A), pulp.value(B),pulp.value(C))
print("Revenue = ", pulp.value(revenue.objective))実行結果
88.0 49.0
2398.0 2350.0 2232.0
Revenue = 1116000.0さて、コードで変わって点からみていきましょう。
製品S用の変数を追加しました。ほかの変数の定義と大きく変わりません。
revenue += (8000-2000)*P + (16000-4000)*S #販売価格 - 材料費 PuLPで最大化する式に、製品Sの売上と材料費を追加して、製品Sと製品Pの数によって利益が変わるように変更しました。
revenue += 15*P + 22*S == A # 各作業者の作業時間の制約
revenue += 10*P + 30*S == B
revenue += 12*P + 24*S == C最後に、各作業者の作業時間も製品Pと製品Sの数によって計算されるようにしました。この制限によって、製品Pと製品Sのどちらを生産した方が好いかが計算できるようになります。
実行した結果をみてみると、利益の数字はたまたま同じになりましたが、製品Pと製品Sの生産数が手計算と少し異なる結果になりました。
手計算では、製品Pを減らす数が13.33個だったので14個減らしました。しかし、製品Pと製品Sの売上が2倍違うため、製品Pを12個減らして製品Sを1個減らすことでも同じ額の利益を出すことができたようです。
とはいえ、結果に大きな差はありません。
工程Aの作業時間を見てみると、2398分でかなりギリギリのところまで使っています。また、製品Sもほぼ最大数まで売ることができています。工程Aと製品Sが制約条件であると考えても好さそうです。
線形計画法を使うことで、面倒な計算を勝手にやってくれるのですごく助かります。もう少しプロセスを複雑にした場合、手計算でやるのは非常に面倒な作業になってしまうでしょう。
もちろんプログラミングの知識が多少必要になりますが、このぐらいだったらそこまで覚えることも多くないのではないでしょうか。
バラツキのあるプロセスの制約条件をベイズ統計学とPuLPで解く
このプロセスはまだまだ複雑にすることができます。
ここまでプロセスを考えるときには、1つの数字で検討してきました。つまり、各生産工程の作業時間はいつでも15分だし、販売できる数も毎週安定した個数を売ることができるという仮定を置いていました。
しかし、現実世界でこのようになることはまずないでしょう。生産工程にはバラツキが存在しますし、売れる個数にもバラツキは存在するはずです。これらを考慮して制約条件を求めることはできないでしょうか?
やってみましょう。今回はプロセスは変えずに、バラツキを追加してみます。つまり、週によって1個あたりの作業時間や販売個数がある分布に従って変わるという仮定を置きます。
これを実行するためにベイズ統計学の考えを取り入れます。
ベイズ統計学を活用してデータを生成する

まずは各工程のデータを作成しましょう。
ベイズ統計学を利用する場合、データ外出どのように生成されるかが重要になってきます。それでは生産工程はどのような分布になっているでしょうか?
まず、作業時間は確実に0以上であるということです。マイナスの作業時間になることはあり得ません。次にこの作業時間は、分単位でデータをとっています。つまり、連続値ではなく離散値となっています。
さらにいうと、生産工程で何も問題が起きていない場合は、正規分布のように左右対称な分布となりますが、問題が発生した時の時間も含めるのであれば、右側の裾が長い分布になることが考えられます。
この条件を満たす分布を使うことで、矛盾のないデータ生成を行いたいところさんです。今回はポアソン対数正規分布を使ってみましょう。
ポアソン対数正規分布は、ポアソン分布のパラメータであるλの対数をとった値が、正規分布に従う分布です。モデル化すると以下のようになります。

まずは仮想的なデータを作ってみます。normalで正規分布からの値を、rpoissでポアソン分布からの値を生成することができます。このとき、平均値はλとなるので、それがプロセスの平均時間になるように設定します。
Rでデータを抽出したい時は以下のようにします。
n = 100
mu <- log(22)
sigma <- 0.1
log_lambda = rnorm(n=n,mean=mu,sd=sigma)
lambda = exp(log_lambda)
A_S = rpois(n=n,lambda=lambda)ただし、これだと行数が多くなってしまうので1行にまとめちゃいます。
A_S = rpois(n=30,lambda=exp(rnorm(n=30,mean=log(22),sd=0.1)))このときnは抽出するデータの数、meanにはlog(平均値)、sdには標準偏差を入れます。sdの値は適当に決めました。
Rコード(生産工程のサンプルデータ生成)
library(ggplot2)
set.seed(1490)
A_S = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(22),sd=0.2)))
B_S = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(30),sd=0.3)))
C_S = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(24),sd=0.5)))
ggplot() +
geom_histogram(aes(x=A_S,y=..density..), fill="springgreen",binwidth=2,alpha=0.4)+
geom_histogram(aes(x=B_S,y=..density..), fill="palevioletred",binwidth=2,alpha=0.4)+
geom_histogram(aes(x=C_S,y=..density..), fill="skyblue",binwidth=2,alpha=0.4)+
labs(x="作業時間",title="製品Sの生産工程の作業時間")+
theme_gray (base_family = "HiraKakuPro-W3")
A_P = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(15),sd=0.5)))
B_P = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(20),sd=0.3)))
C_P = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(12),sd=0.2)))
ggplot() +
geom_histogram(aes(x=A_P,y=..density..), fill="springgreen",binwidth=2,alpha=0.4)+
geom_histogram(aes(x=B_P,y=..density..), fill="palevioletred",binwidth=2,alpha=0.4)+
geom_histogram(aes(x=C_P,y=..density..), fill="skyblue",binwidth=2,alpha=0.4)+
labs(x="作業時間",title="製品Pの生産工程の作業時間")+
theme_gray (base_family = "HiraKakuPro-W3")


ほどよくばらつきのあるデータの生成をすることができました。
Rコード(販売個数のサンプルデータ生成)
set.seed(2590)
P = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(100),sd=0.2)))
S = rpois(n=30,lambda=exp(rnorm(n=n,mean=log(50),sd=0.2)))
ggplot() +
geom_histogram(aes(x=P,y=..density..), fill="springgreen",binwidth=2,alpha=0.6)+
geom_histogram(aes(x=S,y=..density..), fill="palevioletred",binwidth=2,alpha=0.6)+
labs(x="販売個数",title="製品Pと製品Sの販売個数")+
theme_gray (base_family = "HiraKakuPro-W3")
さて、これでばらつきのあるデータが入手できました。材料費に関しては、定期的に仕入れているので、値段は変わらないことにしておきましょう。
今回はデータを生成しないといけないので、あらかじめ分布を設定しましたが、実際にはデータが先にあって、そのデータから分布を導き出さなければなりません。
これらのデータから、ポアソン対数正規分布のパラメータを正しく導き出すことができるかやってみましょう。
データから分布を導き出す方法(Stan)
事前にパッケージの読み込みや、オプションの設定をしておきます。
パッケージの読み込みとオプション設定
library(rstan)
library(bayesplot)
library(ggplot2)
rstan_options(auto_write=TRUE)
options(mc.cores = parallel::detectCores())Rコード(Stanファイルの実行)
A_P_data <- list(
y = A_P,
N = length(A_P)
)
A_P_stan <- stan(
file = "TOC_pois.stan",
data = A_P_data,
iter = 2000,
warmup = 1000,
chain= 4,
)
TOC_pois.stan
data{
int<lower=0> N;
int y[N];
}
parameters {
real mu;
real<lower=0> sigma;
vector[N] log_lambda;
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i] = exp(log_lambda[i]);
}
model {
sigma ~ cauchy(0, 5);
mu ~ normal(0, 10);
log_lambda ~ normal(mu, sigma);
for (i in 1:N)
y[i] ~ poisson(lambda[i]);
}
Stanコードの詳しい説明は行いませんが、前述した以下の式の通りにデータが生成されるようなモデルを実装しているのがわかります。

ちなみにpoisson_logを使えば、expの処理を省くこともできます。
このコードを実行した後に、以下のコードを実行して結果を確かめます。
traceplot(A_P_stan)
mcmc_rhat(rhat(A_P_stan))
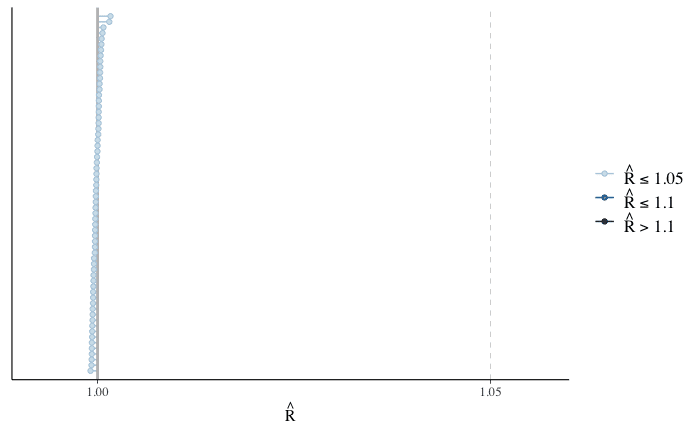
traceplotの結果を見ると、各chainの線が他のchainと重なるようになっており、rhatも1.1よりずっと低い値となっているので問題がなさそうです。
muとsigmaの詳細を見るために以下のコードを使います。y_simは後で使いますが、事後分布からのサンプリングデータです。
print(A_P_stan, pars=c("mu","sigma","y_sim"),probs = c(0.025,0.5,0.975))
A_P_sample <- rstan::extract(A_P_stan, permuted= FALSE)
mcmc_combo(
A_P_sample,
pars = c("mu","sigma","y_sim")
)


A_Pのデータはmean=log(15)=約2.7、sd=0.5で生成しました。推定された平均値や信用区間をみても、それなりの精度で推定されているように見えます。
せっかくなので、ポアソン対数正規分布のグラフを描いて、元のデータとどのぐらい近い分布になっているか確認してみましょう。
ポアソン対数正規分布の分布を作るため、poilogというパッケージを使います。単純にdpoisを使っても好いと思います。
dpoilog関数に推定されたmuとsigmaを引数として渡して、データと同じような分布になっているか確認してみましょう。
library(poilog)
mu = 2.65
sigma = 0.57
X = seq(1,100,by=1)
Y = dpoilog(X,mu,sigma)
ggplot() +
geom_histogram(aes(x=A_P,y=..density..), fill="springgreen",alpha=0.6,bins=20)+
geom_line(aes(x=X,y=Y))
labs(x="作業時間", title="A_Pと予測したポアソン対数正規分布")+
theme_gray (base_family = "HiraKakuPro-W3")
予測した分布を見ると、実際のデータと同じような分布になっていることがわかります。それでは、A_Pと同じように他の工程や販売個数に関しても同様にStanで推定してみましょう。
今回は全て同じ分布を使っているので、同じStanファイルを使うことができます。そのため、Stanに渡すデータのリストだけを変更すれば、他の工程の分布の予測ができます。
結果は省略します。
線形計画法を使って毎週の制約条件を計算する
さて、これで各分布を求めることができました。これであとは、この分布に従って抽出されるサンプルを使って、制約条件を特定することができればいいわけです。
前と同じように、これらの分布から毎週得られる値を線形計画法に流し込めば、制約条件を求めることができます。これは実際のプロセスを何回もシミュレーションすることに似ています。
データが各要素でデータが30個程度しかなくても、分布を作ることで幅広い状況を想定して制約条件を求めることができます。
実際にやってみましょう。
P_sample <- rstan::extract(P_stan)
P_sim <- P_sample$y_sim[1:1000]
A_P_sample <- rstan::extract(A_P_stan)
A_P_sim <- A_P_sample$y_sim[1:1000]
B_P_sample <- rstan::extract(B_P_stan)
B_P_sim <- B_P_sample$y_sim[1:1000]
C_P_sample <- rstan::extract(C_P_stan)
C_P_sim <- C_P_sample$y_sim[1:1000]
S_sample <- rstan::extract(S_stan)
S_sim <- S_sample$y_sim[1:1000]
A_S_sample <- rstan::extract(A_S_stan)
A_S_sim <- A_S_sample$y_sim[1:1000]
B_S_sample <- rstan::extract(B_S_stan)
B_S_sim <- B_S_sample$y_sim[1:1000]
C_S_sample <- rstan::extract(C_S_stan)
C_S_sim <- C_S_sample$y_sim[1:1000]まず、Stanで予測した事後分布からサンプルを抜き出します。これはStanファイルのgenerated quantitiesで設定したものです。
A_P_simの値をグラフにしてみると、ちゃんとA_Pのデータから取得したものと同じ分布になっているのがわかります。ただし、データ数が増えていますね。他のデータも似たような感じです。

さて、データが抽出できたので、あとは線形計画法に流し込むだけです。結果はpandasのDataFrameに保存していきます。
Pythonコード(線形計画法)
import pulp
import pandas as pd
import datetime
start_time = datetime.datetime.now()
df = pd.DataFrame()
for i in range(0,1000):
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=r.P_sim[i])
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=r.S_sim[i])
A = pulp.LpVariable('A', cat="Integer",lowBound=0,upBound=2400) #最大作業時間2400分
B = pulp.LpVariable('B', cat="Integer",lowBound=0,upBound=2400)
C = pulp.LpVariable('C', cat="Integer",lowBound=0,upBound=2400)
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P + (16000-4000)*S #販売価格 - 材料費
revenue += r.A_P_sim[i]*P + r.A_S_sim[i]*S == A # 各作業者の作業時間の制約
revenue += r.B_P_sim[i]*P + r.B_S_sim[i]*S == B
revenue += r.C_P_sim[i]*P + r.C_S_sim[i]*S == C
t = revenue.solve(pulp.PULP_CBC_CMD(msg=0))
temp_df = pd.DataFrame({
"Rev":[pulp.value(revenue.objective)],
"P":[pulp.value(P)],
"S":[pulp.value(S)],
"A":[pulp.value(A)],
"B":[pulp.value(B)],
"C":[pulp.value(C)],
})
df = df.append(temp_df)
df = df.reset_index(drop=True)
end_time = datetime.datetime.now()
print("time:",end_time-start_time)この問題を解くにはそれなりに時間がかかります。今回は約2分程度かかりました。
Rコード(結果表示)
library(reticulate)
summary(py$df)RStudioでRとPythonを使えるようにしているので、上記のRコードでpythonのdfのsummaryを表示できます。
Rev P S A B
Min. : 342000 Min. : 0.00 Min. : 0.00 Min. : 182 Min. : 630
1st Qu.: 696000 1st Qu.: 19.00 1st Qu.:34.00 1st Qu.:1227 1st Qu.:2365
Median : 798000 Median : 38.00 Median :47.00 Median :1610 Median :2386
Mean : 807606 Mean : 45.38 Mean :44.61 Mean :1644 Mean :2275
3rd Qu.: 906000 3rd Qu.: 68.00 3rd Qu.:57.00 3rd Qu.:2111 3rd Qu.:2394
Max. :1668000 Max. :154.00 Max. :92.00 Max. :2400 Max. :2400
C
Min. : 225
1st Qu.:1344
Median :1826
Mean :1772
3rd Qu.:2374
Max. :2400
ばらつきを含めた場合、利益の平均値がだいぶ下がってしまいましたね。
制約条件はどこにある?
各リソースの利用状況を計算されましたが、これだと制約条件になっているのがどこなのかよくわからないですよね。それに、ほぼ上限までリソースを使っている工程が2つ以上あったら、どちらを制約条件としたら好いでしょうか?
ここはシンプルに、全リソースの98%以上を使っていたら、そのリソースを制約条件としてしまいましょう。つまり、工程Aの場合、2400分なので2352分以上使っていたら、制約条件とします。
シミュレーションを1000回実行しているので、その中で制約条件になった回数の割合を計算すれば、制約条件になりやすい工程がわかるかもしれません。
また、2番目や3番目に制約条件になりやすいリソースも把握することができるので、改善の優先順位をつけるのに役立つかもしれません。
length(py$df$A[py$df$A >= 2352])/length(py$df$A)
length(py$df$B[py$df$B >= 2352])/length(py$df$B)
length(py$df$C[py$df$C >= 2352])/length(py$df$C)
length(py$df$P[py$df$P/P_sim >= 0.98])/length(py$df$P)
length(py$df$S[py$df$S/S_sim >= 0.98])/length(py$df$S)[1] 0.173
[1] 0.777
[1] 0.276
[1] 0.131
[1] 0.478一番制約条件になっている割合が高いのは工程Bでした。1000回のうち777回も制約になっています。ここで改善するべき順番を選ぶとすれば、以下の順番になりそうです。
工程Bの作業時間
製品Sの販売数
工程Cの作業時間
工程Aの作業時間
製品Pの販売数
この順番に改善を行なっていくことで、制約条件になる数を減らしやすそうです。
でも本当にその順番で制約条件を減らすことが、利益に対して一番効果が大きいのでしょうか?
制約条件を取り除いた時の利益への影響
せっかくなので、これらの制約条件に対して、改善を行なった場合に利益がどのぐらい伸びるのかもみてみましょう。
ここからは少しずつ"なにに変えるか?"という質問の答えも探していくことになります。
それぞれの工程が2倍改善したと仮定して、利益にどのぐらいの差が出るのかみてみましょう。プログラム的にはやることは簡単で、各変数のupboundの値を2倍にするだけです。
全部の結果はdf_allにまとめていきます。
Pythonコード(製品SのupBoundを2倍)
import pulp
import datetime
import pandas as pd
start_time = datetime.datetime.now()
df_all = pd.DataFrame()
df_new = pd.DataFrame()
for i in range(0,1000):
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=r.P_sim[i])
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=(r.S_sim[i]*2))
A = pulp.LpVariable('A', lowBound=0,upBound=2400)
B = pulp.LpVariable('B', lowBound=0,upBound=2400)
C = pulp.LpVariable('C', lowBound=0,upBound=2400)
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P + (16000-4000)*S #販売価格 - 材料費
revenue += r.A_P_sim[i]*P + r.A_S_sim[i]*S == A # 各作業者の作業時間の制約
revenue += r.B_P_sim[i]*P + r.B_S_sim[i]*S == B
revenue += r.C_P_sim[i]*P + r.C_S_sim[i]*S == C
t = revenue.solve(pulp.PULP_CBC_CMD(msg=0))
temp_df = pd.DataFrame({"S_Rev":[pulp.value(revenue.objective)]})
df_new = df_new.append(temp_df)
df_new = df_new.reset_index(drop=True)
df_all = pd.concat([df_all,df_new],axis=1)
end_time = datetime.datetime.now()
print("time:",end_time-start_time)これを各工程で繰り返して、結果を表示します。
Rコード(結果表示)
summary(py$df_all) S_Rev P_Rev A_Rev B_Rev
Min. : 354000 Min. : 354000 Min. : 354000 Min. : 492000
1st Qu.: 720000 1st Qu.: 690000 1st Qu.: 696000 1st Qu.: 846000
Median : 846000 Median : 798000 Median : 807000 Median : 966000
Mean : 875394 Mean : 815562 Mean : 819480 Mean : 975600
3rd Qu.:1020000 3rd Qu.: 925500 3rd Qu.: 936000 3rd Qu.:1098000
Max. :2028000 Max. :1548000 Max. :1362000 Max. :1722000
C_Rev
Min. : 378000
1st Qu.: 718500
Median : 822000
Mean : 840210
3rd Qu.: 960000
Max. :1470000 ggplot() +
geom_boxplot(aes(x="A",y=py$df_all$A_Rev), colour="springgreen")+
geom_boxplot(aes(x="B",y=py$df_all$B_Rev), colour="skyblue")+
geom_boxplot(aes(x="C",y=py$df_all$C_Rev), colour="tomato")+
geom_boxplot(aes(x="P",y=py$df_all$P_Rev), colour="darkmagenta")+
geom_boxplot(aes(x="S",y=py$df_all$S_Rev), colour="slateblue")+
labs(x="利益", title="各工程を2倍にした時の利益")+
theme_gray (base_family = "HiraKakuPro-W3")
平均利益を向上させる順番で順位をつけるのであれば、以下の優先順位になるでしょう。
工程Bの作業時間
製品Sの販売数
工程Cの作業時間
工程Aの作業時間
製品Pの販売数
制約条件になる割合の順番と同じになりましたね。ただし、この結果は工程のキャパシティを2倍にした時の値なので、他の倍率にした場合は結果が変わるかもしれません。
また、今回はなんの制限もなく、限界数であるupboundを2倍にすることができましたが、実際には改善するためのコストがかかることでしょう。
機械を導入する必要があるかもしれませんし、人を雇う必要があるかもしれません。販売数を伸ばすためには、営業人員を増やさなければならないかもしれませんし、マーケティング予算を増やさないといけないかもしれません。
その場合は、改善にかかるコストを引いて利益を計算しなければなりません。それでは次に、コストについて考えてみましょう。
コストと利益を結びつける
改善を行なった成果とはなんでしょうか?
それは先ほど計算した利益の増加分です。つまり、改善を行った結果、upBoundを2倍にすることができれば、先ほど示した利益が毎週増えることになるわけです。
…であれば、その得られる利益より、改善するコストの方が低いのであれば、総合的に利益が増えるので、その改善は行なった方が好いということがわかります。高額な投資をする場合は、何週間でその投資が回収できるのかも計算できるでしょう。
ここでコスト関数がどのような形をしているのか考えてみましょう。
コスト関数のかたち
コストは増やせば増やしただけ、効果も増えるのでしょうか?そうはならないことが多いでしょう。
今回のプロセスで言えば、1つの工程を改善した結果、その工程が制約条件にならなくなったのであれば、それ以降どれだけコストを増やしたとしても全体の利益には全く影響がありません。
例えば、1000回中800回制約になる工程と200回しかならない工程を考えてみましょう。その工程のキャパシティを伸ばすことができた場合、最初の工程では試行した1000回のうち800回に利益の改善が見込めるでしょう。しかし、2番目の工程では、200回しか改善されません。
仮に改善される1回あたりの利益の額が同じだとしてみましょう。当初の利益が1万円で改善された後の利益は1.2万円になるとします。平均値を計算してみると以下のようになります。
1000回*1万円/1000 = 1
(200回*1万円+800回*1.2万円)/1000= 1.16
(800回*1万円+200回*1.2万円)/1000 = 1.04
最初の工程の平均は16%伸び、2番目の工程は4%しか伸びないわけです。つまり、制約条件になる確率が低くなればなるほど、改善の効果も下がっていきます。
このように効果が徐々に落ちていくことを収穫逓減すると言います。逓減とは少しずつ量が減っていくという意味ですね。
x軸をコストにして、y軸を効果にしたグラフを作成すると以下のようになるでしょう。このようなグラフを投資回収曲線と呼びます。

計量経済学的な予算の配分
製品SとPの販売数、工程A,B,Cの作業時間について、それぞれ改善効果とコストを関数にして表すことを考えます。その関数を線形計画法に組み込むことができれば、どこにどれだけ予算を振り分ければ一番利益を増やすことができるかを求めることができるのではないでしょうか。
まさに"なにに変えるか?"の答えのように思えます。
例えば、予算内でSを1.5倍、Aを1.3倍、Pを1.1倍にすることができて、それが利益を最大化することになるということがわかるのですから。
まずはシンプルな例を考えてみましょう。コストが一定の傾きで増加する関数を作成します。具体的には1単位増えるごとに、固定のコストがかかる以下のような式になります。

これを線形計画法に追加すると、複雑になってきますが、以下のようになります。
Pythonコード(線形計画法+コスト)
import pulp
import pandas as pd
import datetime
start_time = datetime.datetime.now()
df_cost = pd.DataFrame()
for i in range(0,1000):
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=r.P_sim[i])
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=r.S_sim[i])
P_T = pulp.LpVariable('P_T', cat="Integer",lowBound=0)
S_T = pulp.LpVariable('S_T', cat="Integer",lowBound=0)
A_T = pulp.LpVariable('A_T', cat="Integer",lowBound=0)
B_T = pulp.LpVariable('B_T', cat="Integer",lowBound=0)
C_T = pulp.LpVariable('C_T', cat="Integer",lowBound=0)
A = pulp.LpVariable('A', cat="Integer",lowBound=0,upBound=2400)
B = pulp.LpVariable('B', cat="Integer",lowBound=0,upBound=2400)
C = pulp.LpVariable('C', cat="Integer",lowBound=0,upBound=2400)
Y = pulp.LpVariable('Y', cat="Integer",lowBound=0,upBound=100000) # 予算10万円
A_Y = pulp.LpVariable('A_Y', cat="Integer", lowBound=0)
B_Y = pulp.LpVariable('B_Y', cat="Integer", lowBound=0)
C_Y = pulp.LpVariable('C_Y', cat="Integer", lowBound=0)
P_Y = pulp.LpVariable('P_Y', cat="Integer", lowBound=0)
S_Y = pulp.LpVariable('S_Y', cat="Integer", lowBound=0)
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P_T + (16000-4000)*S_T - Y #販売価格 - 材料費
revenue += P + P_Y == P_T
revenue += S + S_Y == S_T
revenue += A + 480*A_Y == A_T
revenue += B + 480*B_Y == B_T
revenue += C + 480*C_Y == C_T
revenue += r.A_P_sim[i]*P_T + r.A_S_sim[i]*S_T == A_T# 各作業者の作業時間の制約
revenue += r.B_P_sim[i]*P_T + r.B_S_sim[i]*S_T == B_T
revenue += r.C_P_sim[i]*P_T + r.C_S_sim[i]*S_T == C_T
revenue += 12000*A_Y + 5000*B_Y + 24000*C_Y + 3500*P_Y + 7000*S_Y == Y
t = revenue.solve(pulp.PULP_CBC_CMD(msg=0))
temp_df = pd.DataFrame({
"Rev":[pulp.value(revenue.objective)],
"P_T":[pulp.value(P_T)],
"S_T":[pulp.value(S_T)],
"P":[pulp.value(P)],
"S":[pulp.value(S)],
"A":[pulp.value(A)+480*pulp.value(A_Y)],
"B":[pulp.value(B)+480*pulp.value(B_Y)],
"C":[pulp.value(C)+480*pulp.value(C_Y)],
"Y":[pulp.value(Y)],
"A_Y":[pulp.value(A_Y)],
"B_Y":[pulp.value(B_Y)],
"C_Y":[pulp.value(C_Y)],
"P_Y":[pulp.value(P_Y)],
"S_Y":[pulp.value(S_Y)]
})
df_cost = df_cost.append(temp_df)
end_time = datetime.datetime.now()
print(end_time-start_time)
各工程の合計値は"_T"のついている変数で表しています。例えば、製品PのP_Tは何もしないで売れる販売数に、予算を追加して増えたP_Yを足した合計になっています。
生産工程の場合は、A_Yが1単位増えるごとに480分作業時間が増えるようにしました。
"工程_Y"を1単位増やすには以下の式にあるコストがかかります。このコストは最大予算額であるYによって制限されています。
revenue += 12000*A_Y + 5000*B_Y + 24000*C_Y + 3500*P_Y + 7000*S_Y == Yこれによって、予算10万円を使った時、どの工程にどれぐらいの予算を使うべきなのかがシミュレーションごとにわかります。結果は以下のようになりました。

しかし、これだと最終的にどんな予算の配分にすれば、最適になるのかがわかりません。
毎週毎週、予算の配分を変更することができるならこれでもいいのですが、多くの企業ではそうもいかないでしょう。もし人を雇うなら週単位で働いてくれる人を見つけることになりますし、機械に投資したのであれば、キャパシティはずっと高いままになるでしょう。
…であれば、予算の配分をある程度固定した時に、利益が最大化される組み合わせを見つけたいということになります。しかし、それを全探索しようとすると計算数が膨大になってしまいます。
各"工程_Y"の値が30通りあったとしたら、30^5回(=2430万回)シミュレーションを行わなければなりません。このシンプルなプロセスであっても、そんなに時間がかかるのであれば、複雑なプロセスの計算はできなくなってしまうでしょう。
遺伝的アルゴリズムで最適化問題を解く
さて、この問題に対して、最適な組み合わせを見つけるには、どのようにするのが好いでしょうか。それぞれ何個か使うことができて、それぞれの値によって合計の値を導き出す。…ナップザック問題に似ていますよね。
ナップザック問題の場合、合計の重さが一定以上を超えないように、持てるものの価値を最大化します。これを今回の問題に応用すると、合計の予算が一定以上を超えないように、利益を最大化するような問題を設定します。
常に最適な値を導き出せるわけではありませんが、現実的な時間で最適な値に近い値を求めたいのであれば、遺伝的アルゴリズムを使うことができます。
遺伝的アルゴリズムの説明
遺伝的アルゴリズムは、生物のDNAが交叉したり変異したりする過程を再現するようなアルゴリズムです。詳細な説明はここでは行いませんので、もう少し詳しい内容を知りたい方はWikipediaの記事などを見てみてください。
ある場所に個体数N=40匹いる牧場があるとします。ここにいる動物は以下の3つの方法で次の世代を作ることになります。
2匹の個体が交配して、親の遺伝子を受け継いだ子供を生み出す
1匹の個体が突然変異して、遺伝子が変化します。
1匹の個体は何も変わらず、そのまま残ります。
この方法のどれかをランダムに利用して、次世代の個体数がNになるまで繰り返します。これを世代数G繰り返して、その中から最適な遺伝子を問題の答えとします。
遺伝的アルゴリズムの実装
遺伝的アルゴリズムを実装するためにDEAPライブラリを活用します。詳細な使い方はここでは説明しませんので、DEAPのウェブサイトを確認してください。
まずは何を遺伝子とするかを決めます。遺伝子は求めたい問題の答えなので、今回は"工程_Y"の値を遺伝子とします。
遺伝子 = [A_Y, B_Y, C_Y, P_Y, S_Y]
この組み合わせのうち、どの組み合わせが利益を最大化するかを求めたいわけです。
そのためは2つの条件があります。"工程_Y"の組み合わせによって予算である10万円を超えないこと、そして利益が最大化されているかです。
これで問題が定義できたので、さっそくDEAPで実装します。
Pythonコード(DEAPでの遺伝的アルゴリズムの実装)
import deap
import pulp
import statistics
import numpy
import datetime
from deap import base,creator,tools,algorithms
import random
start_time = datetime.datetime.now()
creator.create("FitnessMax",base.Fitness,weights=(1.0,-1.0,))
creator.create("Individual", list, fitness = creator.FitnessMax )
items = [12000,5000,24000,3500,7000] #A_Y,B_Y,C_Y,P_Y,S_Y
MAX_BUDGET = 100000
def evalRevenue( individual ):
y = 0.0
for i in range(len(items)):
y += items[i]*individual[i]
if y > MAX_BUDGET:
return -1,1000000,
mean_revenue = calcMeanRevenue(individual,y)
return mean_revenue,y,
def calcMeanRevenue(individual,y):
revenue_list = []
for i in range(0,50):
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=(r.P_sim[i]+individual[3]))
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=(r.S_sim[i]+individual[4]))
A = pulp.LpVariable('A', lowBound=0,upBound=(2400+480*individual[0]))
B = pulp.LpVariable('B', lowBound=0,upBound=(2400+480*individual[1]))
C = pulp.LpVariable('C', lowBound=0,upBound=(2400+480*individual[2]))
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P + (16000-4000)*S - y #販売価格 - 材料費
revenue += r.A_P_sim[i]*P + r.A_S_sim[i]*S == A# 各作業者の作業時間の制約
revenue += r.B_P_sim[i]*P + r.B_S_sim[i]*S == B
revenue += r.C_P_sim[i]*P + r.C_S_sim[i]*S == C
t = revenue.solve(pulp.PULP_CBC_CMD(msg=0))
revenue_list.append(pulp.value(revenue.objective))
return statistics.mean(revenue_list)
toolbox = base.Toolbox()
toolbox.register("attribute", random.randint, 0,10)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attribute, len(items))
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("select", tools.selTournament, tournsize=5)
toolbox.register("mate", tools.cxOnePoint)
toolbox.register("mutate", tools.mutUniformInt,low=0,up=30,indpb=0.2)
toolbox.register("evaluate", evalRevenue)
random.seed(128)
NGEN = 10
POP = 40
CXPB = 0.9
MUTPB = 0.1
pop = toolbox.population(n=POP)
for ind in pop:
ind.fitness.values = toolbox.evaluate(ind)
hof = tools.ParetoFront()
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("max", numpy.max, axis=0)
algorithms.eaSimple(pop, toolbox, cxpb=CXPB, mutpb=MUTPB, ngen=NGEN,stats=stats, halloffame=hof)
best_ind = tools.selBest(pop, 1)[0]
print(best_ind, best_ind.fitness.values)
end_time = datetime.datetime.now()
print(end_time-start_time)各遺伝子の評価方法をevalRevenue関数で実装しています。利益を計算するのは時間がかかるので、もし最大予算を超える組み合わせであれば、すぐに予算を超えたとわかるようにしています。
もし予算内の組み合わせなら、calcMeanRevenue関数で、各シミュレーションの平均利益を計算し、それを遺伝子の価値に設定しています。
基本的に遺伝子的アルゴリズムは実行に時間がかかります。個体数や世代数を少なく設定していますが、20分程度かかります。
実行結果
printbest_ind, best_ind.fitness.values)
>>> [2, 5, 0, 0, 2], (1002840.0, 63000.0)
print(end_time-start_time)
>>> 0:20:58.035790今回の場合、A_Y=2, B_Y=5, S_Y=2にすると、予算を6万3千円使い、利益を平均して約100万円にできることがわかりました。
ベイズ最適化で最適化問題を解く
ベイズ最適化はある関数f(x)が最大値/最小値になるxを求めたい時に使います。特に関数の計算処理が多い場合に便利と言われています。
ベイズ最適化はまだ説明できるほど詳しくないので、とりあえず使ってみた感じです。なのでPythonで実行した結果を見ていきます。
Pythonコード(ベイズ最適化)
import numpy as np
import GPyOpt
import math
import pulp
import statistics
import datetime
start_time = datetime.datetime.now()
items = [12000,5000,24000,3500,7000] #A_Y,B_Y,C_Y,P_Y,S_Y
MAX_BUDGET = 100000
def evalRevenue( individual ):
y = 0.0
for i in range(len(items)):
y += items[i]*individual[:,i]
if y > MAX_BUDGET:
return -1
mean_revenue = calcMeanRevenue(individual,y)
return mean_revenue
def calcMeanRevenue(individual,y):
revenue_list = []
for i in range(0,1000):
P = pulp.LpVariable('P', cat="Integer",lowBound=0,upBound=(r.P_sim[i]+individual[:,3]))
S = pulp.LpVariable('S', cat="Integer",lowBound=0,upBound=(r.S_sim[i]+individual[:,4]))
A = pulp.LpVariable('A', lowBound=0,upBound=(2400+480*individual[:,0]))
B = pulp.LpVariable('B', lowBound=0,upBound=(2400+480*individual[:,1]))
C = pulp.LpVariable('C', lowBound=0,upBound=(2400+480*individual[:,2]))
revenue = pulp.LpProblem(sense=pulp.LpMaximize) #最大化問題を解く
revenue += (8000-2000)*P + (16000-4000)*S - y #販売価格 - 材料費
revenue += r.A_P_sim[i]*P + r.A_S_sim[i]*S == A# 各作業者の作業時間の制約
revenue += r.B_P_sim[i]*P + r.B_S_sim[i]*S == B
revenue += r.C_P_sim[i]*P + r.C_S_sim[i]*S == C
t = revenue.solve(pulp.PULP_CBC_CMD(msg=0))
revenue_list.append(pulp.value(revenue.objective))
return statistics.mean(revenue_list)
bounds = [{'name': 'A_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[0])))},
{'name': 'B_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[1])))},
{'name': 'C_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[2])))},
{'name': 'P_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[3])))},
{'name': 'S_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[4])))}]
opt = GPyOpt.methods.BayesianOptimization(f=evalRevenue, domain=bounds,maximize=True)
opt.run_optimization(max_iter=10000)
print(opt.x_opt, opt.fx_opt)
end_time = datetime.datetime.now()
print(end_time-start_time)pip install gpy
pip install gpyoptまずGpyとGPyOptをインストールしておく必要があります。
evalRevenue関数はほぼそのまま使うことにします。この関数から得られる値を最大化するようにベイズ最適化を実行してみます。
bounds = [{'name': 'A_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[0])))},
{'name': 'B_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[1])))},
{'name': 'C_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[2])))},
{'name': 'P_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[3])))},
{'name': 'S_Y', 'type': 'discrete', 'domain': tuple(range(0, math.ceil(MAX_BUDGET/items[4])))}]各変数は離散値で0から、10万円で増やせる最大数までとしました。
print(opt.x_opt, opt.fx_opt)
>>> [ 1. 11. 1. 2. 0.] -1006126.0
print(end_time-start_time)
>>> 0:12:51.111405こちらで計算してみると、A_Y=1, B_Y=11, C_Y=1, P_Y=2で、予算を98,000円使って、こちらも利益を約100万円に増やすことができています。
どちらの方法でも、もっと複雑なプロセスになると計算が難しくなりそうです。
まとめ
改善前の分布と、遺伝的アルゴリズムで計算した改善後の利益の分布のグラフを見てみます。

利益は増えていますが、ばらつきが増えている感じですね。ちなみに差分を取ってみると、約81%が0より大きいの値になっています。つまり、81%の確率で利益が向上しています。
ちなみにベイズ最適化の組み合わせを使った場合の差分は約89%が0より大きい値になっています。
まだまだ検討の余地がたくさんありそうです。まる。
ここまで読んでいただけたなら、”スキ”ボタンを押していただけると励みになります!(*´ー`*)ワクワク
