【電子工学】キルヒホッフの法則とグラフ理論

1.はじめに

　本記事では, 回路解析への入門として, 電気回路における重要な法則であるキルヒホッフの法則とグラフ理論の関わりについて扱う. 
　グラフ理論におけるグラフとは, ある「点」とそれにつながる「辺」から構成される幾何学的対象のことをいう.
　グラフ理論は, モノとモノのつながりの情報に注目し, そこから様々な性質を分析できる特性やコンピュータ処理との親和性の高さから, 数学的基礎研究のみならず, 回路解析やコンピュータサイエンス, 社会ネットワーク分析, 路線図問題といった幅広い領域に応用されている.
　本記事では, 次節においてキルヒホッフの法則を復習したうえで, 第3節ではグラフ理論の諸定義を与え, 第4節において回路解析への入門として, キルヒホッフの第1法則と第2法則をそれぞれグラフ理論における基本カットセット行列, 基本タイセット行列によって表現することを目標とする.

2.キルヒホッフの法則

本節では, キルヒホッフの法則について確認する. 尚, 第1法則は電流則(KCL: Kirchhoff’s Current Law), 第2法則は電圧則(KVL: Kirchhoff’s Voltage Low)ともよばれる.

命題2.1（キルヒホッフの第1法則）
　電気回路の任意の分岐点において, 流入する電流の和と流出する電流の和は等しい.

命題2.2（キルヒホッフの第2法則）
　電気回路の任意の閉回路において, 起電力と電圧降下の和は等しい. ここで, 起電力とは電源の電圧（電位の差）, 電圧降下とは抵抗の電圧のことをいう.

3.グラフ理論超入門

　本節では, 次節で扱う回路解析に向けた準備として, グラフ理論の諸定義を紹介する.

定義3.1（集合と部分集合）
　あるモノや数の集まりを集合といい, その集合に含まれるモノや数を要素という. また, 集合の一部を部分集合という.

定義3.2（直積集合）
　2つの集合$${A}$$, $${B}$$が与えられたとき, $${A}$$と$${B}$$それぞれからひとつずつ要素を取り出した組の集合を$${A×B}$$と表し, $${A}$$と$${B}$$の直積集合という.

定義3.3（グラフ）
　${V}$$を点の集合, $${E}$$を辺の集合としたとき, $${G=(V,E)}$$をグラフとよぶ. ただし, $${E}$$は直積集合$${V×V}$$の部分集合である.
　また, 辺が向きづけされていないグラフを無向グラフ, 辺が向きづけされているグラフを有向グラフという.
　さらに, 全ての点とつながっている辺集合のうち, 辺の数が最小であるものを木といい, また, 木に含まれない辺を補木という.

定義3.4（基本カットセット）
　任意の2つの点が辺でつながっているグラフを連結グラフという.
ある1つの連結グラフから, 特定の辺が取り除かれると2つの連結グラフに分割されるとき, そのような辺の集合をカットセットとよぶ.
　特に, 木の辺を1つだけ含むカットセットを基本カットセットという.

定義3.5（基本タイセット）
　補木の辺を1つ含み, それ以外は木の辺であるような閉路を基本タイセットという.

4.グラフ理論によるキルヒホッフの法則の表現

　本節では, 前節で定義したグラフ理論における基本カットセットと基本タイセットを活用してキルヒホッフの法則を表現する. 例として, 以下のような有向グラフで表される回路を考える.

図1. 有効グラフ

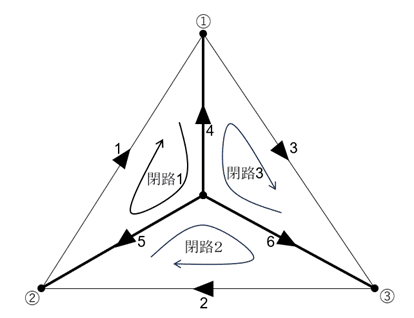
　但し, 辺$${ \{ 4,5,6 \} }$$から構成される集合を木とする. このとき, 基本カットセット行列$${C}$$を以下で表現することができる.

尚, 各行はそれぞれ辺4を含む基本カットセット, 辺5を含む基本カットセット, 辺6を含む基本カットセットを表し, 列は左から順に辺1~6に対応する. 特に, その辺が基本カットセットに該当しない場合は0, その辺が基本カットセットに該当する場合, 各行に含まれる木の辺と同じ向きであれば1, 逆の向きであれば-1とする.
このとき, キルヒホッフの第1法則を, 基本カットセット行列$${C}$$と辺1~6に対応する電流ベクトル$${i=[i_1,\cdots,i_6 ]^T}$$を用いて$${Ci=0}$$で表すことができる.
次に, 第2法則を考えるため, 基本タイセットの行列表現を考えよう.
　図1について, 基本タイセット行列を以下で表すことができる.

　尚, 各行はそれぞれ閉路1~3に対応する基本タイセットを表し, 列は左から順に辺1~6と対応する. 特に, その辺が基本タイセットに該当しない場合は0, その辺が基本タイセットに該当する場合, 閉路と同じ向きであれば1, 逆の向きであれば-1とする.
　このとき, キルヒホッフの第2法則を, 基本タイセット行列Bと辺1~6に対応する電圧ベクトル$${v=[v_1,\cdots,v_6 ]^T}$$を用いて$${Bv=0}$$で表すことができる.

参考文献

[1] 篠田庄司, Ⅲ.回路解析, 電気学会雑誌 100(2): 100-105, 1979.
[2] 成嶋　弘, マグロウヒル大学演習 離散数学 コンピュータサイエンスの基礎数学, オーム社, 2017.
[3] R. Diestel, Graph Theory, Springer, 2005.