
M1グランプリ トップバッター不利説は本当か?ジニ係数を求めてみた
こんばんは、二階からラグランジュ関数です。
世の中は格差に溢れています。
所得格差、教育格差、地域格差、男女格差、
そしてそれに引けを取らないM1格差
漫才の頂点を決めるM1グランプリですが、
「トップバッターから優勝するのは相当厳しい」
「出順によって勝敗がかなり左右される」
などの意見があります。
これは本当なのでしょうか?
本記事ではこの、M1格差が本当に存在するのか、検証していきます。
データを見てみる
出順ごとの最終決戦(3組で行われるやつ)進出者数を、Wikiを基にカタカタ集計してみました。
M1グランプリでは9組のファイナリストが存在する2002~2016年と、10組存在する2017年~2021年に大別される為、これらを分けて考えます。
また、2001年は最終決戦という概念のない年なので、こちらは除外して考えます。
2002~2016年
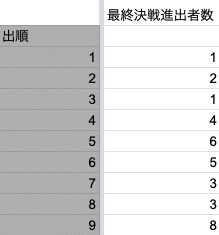
2017~2022年
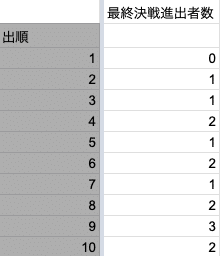
うーむ、、確かに出順が後半になるにつれ、最終決戦に勝ち残りにくい傾向は見えますね。
格差を定量化する
ジニ係数とはご存知でしょうか?
ざっくり、格差の度合いを定量化するための指標になります。
ジニ係数(ジニけいすう、英: Gini coefficient)とは主に社会における所得の不平等さを測る指標である。0から1で表され、各人の所得が均一で格差が全くない状態を0、たった一人が全ての所得を独占している状態を1とする。 (Wikipedia)
「所得格差」を考えるとき、「均等分布線(完全平等線)」と「ローレンツ曲線」の2つが重要になります。
所得の低い世帯から順に、所得を足し合わせていくとき、もしも世の中が完全に平等、誰もが同じ所得であるならば、世帯累積比が大きくなるにつれて所得累積比も線形に大きくなるはずです。これを表すのが均等分布線です。
しかし実際にはそうなっておらず、所得の低い世帯と高い世帯が存在します。低所得世帯の所得を足し合わせていく段階では傾きは45度よりも緩やかに、高所得世帯では急になるはずです。これを表すのがローレンツ曲線です。
この均等分布線(格差のない世界線)とローレンツ曲線(実際)の差分がジニ係数ということになります。
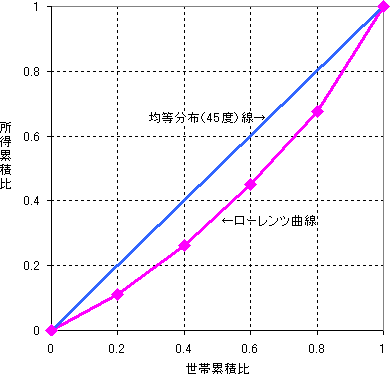
M1に適用してみる
さて、これを用いてM1グランプリのジニ係数を求めてみましょう。
今回は「所得による格差」ではなく「出順による格差」です。
2002~2016年のもの。
左から、先ほどお見せした最終決戦進出者数、それを少ない順に並び替えたもの、それを累計したもの、その比率、決勝進出者数(2011~2014年未開催ということもあり11年分なので、各順位に対して11名)、その累計、その比率となっています。

もしも出順によって差がないのなら、どの出順でも等しい確率で最終決戦に残れるはずです。
先ほどの説明に当てはめると、
累計決勝進出者比率=均等分布線、
累計最終決戦進出者比率=ローレンツ曲線
となります。
実際にプロットしてみた結果がこちらです。

2017~2021年も見てみましょう。
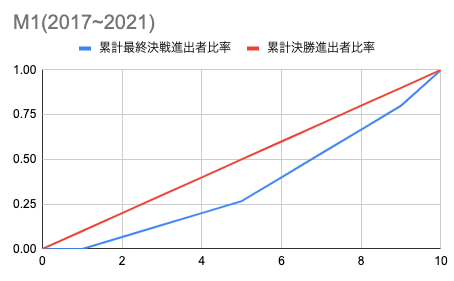
下に出来ている台形の面積計算して足し合わせて三角形から引いて...ってやっていくとジニ係数を算出出来ます。
結果は、、、
2002~2016年 → 0.33
2017~2022年 → 0.28
これ、国ごとの所得格差でいくとどれぐらいに当たるんでしょうか?
2019年のデータで報告されている42か国において、
第1位 南アフリカ (0.62)
第16位 日本 (0.33)
第33位 スウェーデン (0.28)
第42位 スロバキア (0.22)
2002~2016年は日本と同じぐらい、2017~2022年はスウェーデンと同じぐらいという結果になりました。
おわりに
スウェーデンというと福祉国家として有名ですよね。こう考えると、M1グランプリの出順に格差がある、と訴えるのはどうなんでしょうか。
M1グランプリに格差は少ないのか、それとも世界に格差がありすぎるのか。
こんな難しい話をしたいわけではなく、
ただただジニ係数使って遊んでみたかっただけなのです。
