見出し画像

Processing でマイクラ②　マイクラ建築を自動化してみよう

creativival

前回に引き続き、Processing x Minecraft を書いていきます。
マイクラは楽しいんだけど面倒くさいなと思ったことありませんか？　例えば巨大な建築を作るため、整地作業が必要になったとします。サイズは100x100の平面が必要です。延々とブロック崩しをしなくてはなりません。土を削り岩を削り、木を切り倒して邪魔なブロックを除いていきます。油断していると地面を掘りすぎて埋め戻しをしたり、あと何個削るかわからなくなったり、頭がおかしくなりそうです（こういった作業が苦でない人もおられるんでしょうね。私は特に苦手です）。
こういうときはチート（＝プログラミング）しましょう。Rapsberry Jam Mod を入れて、以下のコードで一発、整地が完了します。たったの４行です。（setBlocksコマンドは、指定した範囲内にすべて同じブロックを置くことができます。）

import mcpi.minecraft as minecraft
mc = minecraft.Minecraft.create()
x, y, z = mc.player.getPos()
setBlocks(x - 50, y, z -50, x + 50, y + 50, z + 50, 0)  # AIR

プログラミングのパワーを使って、マイクラ建築の自動化を進めましょう。
今回は、Processing + Minecraft = Processincraft で建築をして遊びます。

チェック模様の床（条件分岐）

# チェック模様の床
for i in range(20):
    for j in range(20):
        wool_id = 35
        if (i + j) % 2 == 0:
            sub_wool_id = 0
        else:
            sub_wool_id = 15
        block_positions.append((i, 0, j, wool_id, sub_wool_id))
checked_floor1

チェックの床は案外面倒です。一つ置きに色を変えたブロックを置かなくてはならないからです。プログラミングでは、if (i + j) % 2 == 0　の条件式を使って、色を自動で切り替えることができます。

for i in range(20):
    for j in range(20):
        wool_id = 35
        # if (i + j) % 2 == 0:
        #     sub_wool_id = 0
        # else:
        #     sub_wool_id = 15
        if (i + j) % 3 == 0:
            sub_wool_id = 0
        elif (i + j) % 3 == 1:
            sub_wool_id = 2
        else:
            sub_wool_id = 15
        block_positions.append((i, 0, j, wool_id, sub_wool_id))
checked floor2

３色を使った床を作りました。先ほどのコードを少し修正するだけで、３色チェック模様を描くことができました。４色、５色、６色のチェック模様も同じ方法で作れますよ。

らせん階段（タートルグラフィックス）

# タートルグラフィック
class Turtle:
    def __init__(self):
        self.position = [0, 0, 0]
        self.yaw = 0
        self.pitch = 90
        self.color = 0
        self.drawable = True

    def forward(self, distance):
        direction = [
            distance * sin(radians(self.pitch)) * cos(radians(-self.yaw)),
            distance * cos(radians(self.pitch)),
            distance * sin(radians(self.pitch)) * sin(radians(-self.yaw)),
        ]
        max_direction = max(map(abs, direction))

        for i in range(int(ceil(max_direction))):
            sd = scalar_direction(direction, i / max_direction)
            x = self.position[0] + sd[0]
            y = self.position[1] + sd[1]
            z = self.position[2] + sd[2]
            if x > 0:
                x = int(x + 0.0001)
            else:
                x = int(x - 0.0001)
            if y > 0:
                y = int(y + 0.0001)
            else:
                y = int(y - 0.0001)
            if z > 0:
                z = int(z + 0.0001)
            else:
                z = int(z - 0.0001)
            block_positions.append((x, y, z, 35, self.color))
        self.position = [
            self.position[0] + direction[0],
            self.position[1] + direction[1],
            self.position[2] + direction[2],
        ]

    def rotate(self, angle):
        self.yaw += angle

    def tilt(self, angle):
        self.pitch -= angle

    def penup(self):
        self.drawable = False

    def pendown(self):
        self.drawable = True

    def pencolor(self, pen_color):
        self.color = pen_color  # 0から15（羊毛の色）

    def home(self):
        self.position = [0, 0, 0]
        self.yaw = 0
        self.pitch = 90
        self.color = 0
        self.drawable = True

    def setpos(self, x, y, z):
        self.position = [x, y, z]

def scalar_direction(d, scalar):
    return [
        d[0] * scalar,
        d[1] * scalar,
        d[2] * scalar
    ]

「らせん階段」建築の準備として、Turtleクラス を作成します。「タートルグラフィックス」は、プログラミングの入門によく使われるお絵描きプログラムです。タートルグラフィックスに含まれるたくさんの機能のうち、今回使うものだけ実装しています。

# らせん階段
t = Turtle()
t.tilt(15)
for _ in range(12):
    t.pencolor(t.color + 1)
    t.forward(20)
    t.rotate(90)

クラフトデータを作成します。tilt(15) で角度を上向きに変えます。forward(20)で 20ブロック前進して、rotate(90) で角度を90度回す。これを12回繰り返します。ペンの色は羊毛で再現しており、回転ごとに一つずつ増やしています。

spiral steps

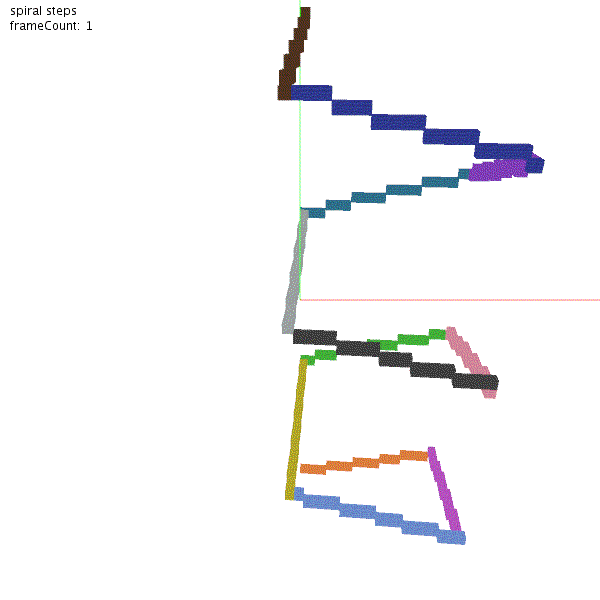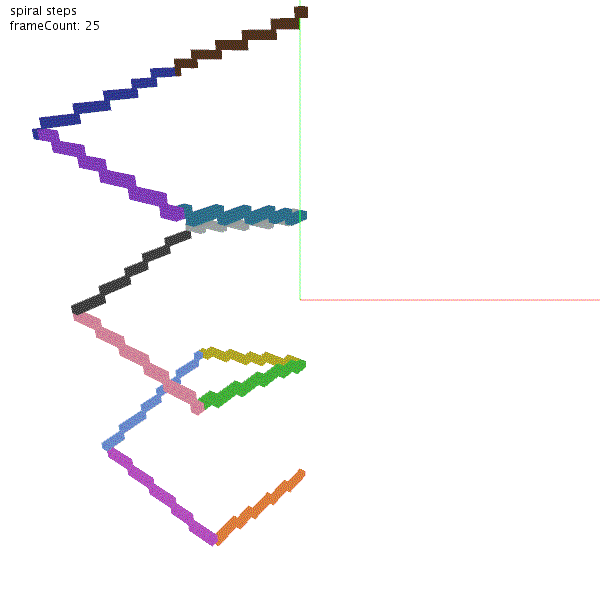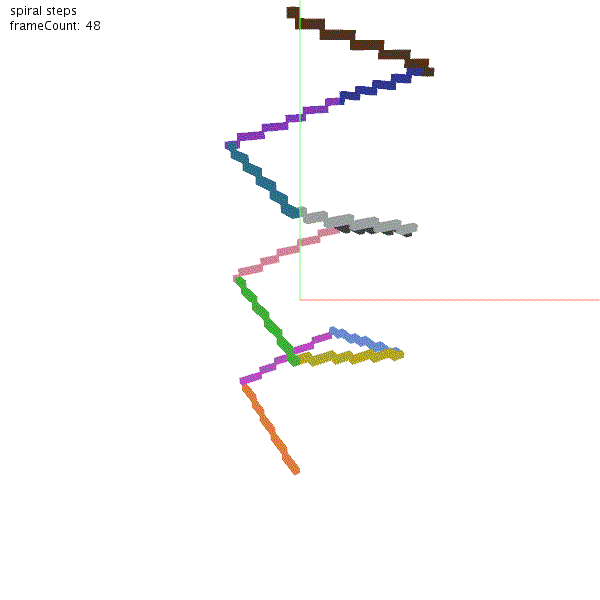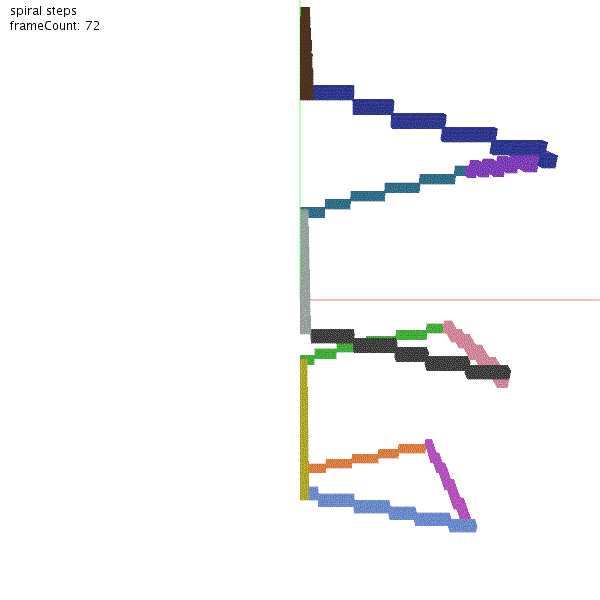
鳥かご（タートルグラフィックス）

# 鳥かご
t = Turtle()
for i in range(36):
    t.rotate(i * 10)
    t.pencolor(i % 16)
    for _ in range(36):
        t.forward(5)
        t.tilt(10)
    else:
        t.home()

Turtleクラスを使うと、様々な建築を行うことができます。次は「鳥かご」を作ってみましょう。らせん階段のプログラムと似ていますが、for文が二重になっています。中のfor文で円を描き、外のfor文で角度を10度ずつ変化させています。
for文のelse以降には、繰り返しの最後だけ実行したいコードを書きます。今回は、home()を実行して、繰り返しによる誤差をなくす工夫をしています。

bird cage

フラクタルツリー（再起関数）

    # フラクタルツリー
    branch_count = 5
    branch_length = 20
    t = Turtle()
    t.pencolor(12)
    t.tilt(90)
    t.forward(branch_length)
    branch(t, branch_length, branch_count)


def branch(_t, _length, _count):
    # 左分岐
    t1 = Turtle(_t)
    t1.pencolor(13)  # green
    t1.tilt(30)
    t1.forward(_length)
    # 右分岐
    t2 = Turtle(_t)
    t2.pencolor(5)  # lime
    t2.tilt(-30)
    t2.forward(_length)

    if _count > 0:
        branch(t1, _length * 0.7, _count - 1)
        branch(t2, _length * 0.7, _count - 1)

フラクタル図形の中でもとくに有名な「フラクタルツリー」を描いてみます。フラクタルツリーは「再起関数」を使うと簡単に描くことができます。
再起関数とは「自分自身」を呼び出す関数のことです。合わせ鏡のように自分自身に自分自身を含み、無限に繰り返す関数です（ちょっと不気味ですね）。無限に繰り返すと計算が終わらないので作画できません。変数branch_countを実行ごとに減らすことで、branch_count == 0 のとき無限ループから脱出します。繰り返しごとに枝の長さを短くすると、本物の木に近づけることができます。

fractal tree

条件分岐、タートルグラフィックス、フラクタル、再起関数を駆け足で見てきました。もっとたくさん作りたいものがあるのですが、長くなりましたので今回は終わりにいたします。
Processing + Minecraft = Processincraft の記事は続きます。

前の記事
Processing でマイクラ① マイクラ風の家を建築
次の記事
Processing でマイクラ③　Processingからマイクラにデータを送信

その他のタイトルはこちら


いいなと思ったら応援しよう！