
Processing でグラフを描く⑱ 遺伝的アルゴリズム(前編)
Processing でグラフを描く 第18回目です。
遺伝的アルゴリズムは生物の進化の過程をシミュレートして、複雑な問題の解を求めるプログラムのことです。通常のアルゴリズムでは時間がかかりすぎて扱えない問題であっても、遺伝的アルゴリズムを適用するとコンピューターで処理して有益な解答を導き出すことができるのです。
非常に興味深い分野ですが、「生物の進化をシミュレートする」と言われてもイメージが湧きづらいと思います。そこで今回は「ドット絵の頂点をつなぐ経路を見つける」という具体的な題材をもとに遺伝的アルゴリズムを説明します。
今回の「遺伝的アルゴリズム」はかなりの文章量になります。前編、後編の2回に分けてお伝えしていきます。
ドット絵の頂点データ
BACKGROUND_COLOR = color(0, 44, 77)
SIZE = 1000
STEP = 200
# ドット絵の頂点
vertexes = [
(23, 1),
(39, 1),
(21, 3),
(23, 3),
(25, 4),
(27, 4),
(39, 3),
(41, 3),
(25, 6),
(27, 6),
(31, 12),
(41, 12),
(31, 14),
(37, 14),
(29, 16),
(37, 16),
(1, 16),
(3, 16),
(19, 16),
(21, 16),
(16, 18),
(19, 18),
(3, 20),
(5, 20),
(13, 20),
(16, 20),
(29, 20),
(33, 20),
(29, 22),
(31, 22),
(5, 22),
(7, 22),
(11, 22),
(13, 22),
(31, 24),
(33, 24),
(7, 24),
(11, 24),
(1, 28),
(3, 28),
(27, 29),
(29, 29),
(3, 30),
(5, 30),
(5, 32),
(7, 32),
(25, 32),
(27, 32),
(7, 34),
(9, 34),
(23, 34),
(25, 34),
(9, 36),
(11, 36),
(17, 36),
(19, 36),
(15, 38),
(17, 38),
(19, 38),
(21, 38),
(13, 40),
(15, 40),
(13, 42),
(15, 42),
(23, 42),
(25, 42),
(11, 44),
(15, 44),
(21, 44),
(25, 44)
]
def setup():
size(SIZE, SIZE)
def draw():
background(BACKGROUND_COLOR)
noFill()
for i in range(int(SIZE / STEP)):
stroke(0, 255, 0, 50)
line(-2000, i * STEP, 2000, i * STEP)
line(i * STEP, -2000, i * STEP, 2000)
for j in range(10):
stroke(0, 255, 0, 25)
line(-2000, i * STEP + j * STEP / 10.0, 2000, i * STEP + j * STEP / 10.0)
line(i * STEP + j * STEP / 10.0, -2000, i * STEP + j * STEP / 10.0, 2000)
# ドット絵の頂点をつなぐ
stroke(127)
for i in range(len(vertexes)):
x0 = vertexes[i][0] * STEP / 10.0
y0 = vertexes[i][1] * STEP / 10.0
x1 = vertexes[(i + 1) % len(vertexes)][0] * STEP / 10.0
y1 = vertexes[(i + 1) % len(vertexes)][1] * STEP / 10.0
line(x0, y0, x1, y1)
ellipse(x0, y0, 2, 2)
text(str(i), x0 + 10, y0)
「ドット絵をグラフにする」の回で、ドット絵から頂点の座標を取得する方法を紹介しました。頂点の数は 70個あります。70個の頂点をリストの順番で線を引きました。ジグザグの線が描かれただけで、恐竜の形にはなりませんでした。頂点をつなぐ順番を変更しなくてはなりません。
今回の課題は、頂点をつなぐ順番を見つけることです。この問題は「巡回セールスマン問題(Traveling Salesperson Problem)として有名です。一見単純なこの問題は、コンピューターの計算能力を持ってすれば、簡単に解けてしまうと思えます。しかし通常の方法ではコンピューターで扱うことができないのです。それはなぜでしょうか?
巡回セールスマン問題
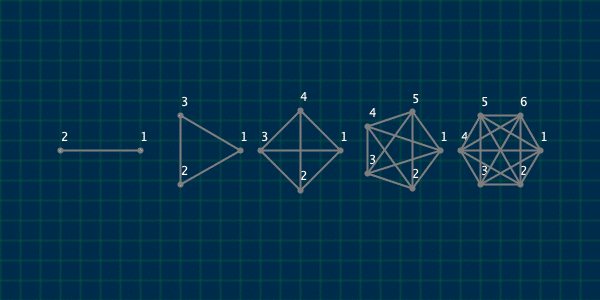
巡回セールスマン問題は、セールスマンがすべての都市を訪問し最初の都市に戻るまでの最短のコースを求める問題です。都市の数が2つ、3つのときは経路は1つしかありません。都市の数が4つになると、経路は $${(1,2,3,4,1) (1,2,4,3,1) (1,3,4,2,1)}$$の3つになります。都市の数が5つのときは経路は12通り、6つのときは60通りと急速に増えていきます。
都市の数が n のとき、$${\frac{(n-1)!}{2}}$$ 通りの経路が考えられます。都市の数が10のときは、$${181,440}$$ 通り、20のときは $${60,822,550,204,416,000}$$ 通りです。この処理をコンピューターで計算しようとすると、何百年もかかってしまいます。もっと多くなったら? 現実的にコンピューターでは処理できないとわかるでしょう。
今回の課題「ドット絵の頂点をつなぐ経路を求める」を巡回セールスマン問題に置き換えて考えます。頂点(都市)の数が70もありますから、かなりの難問ですが、遺伝的アルゴリズムで立ち向かっていきます。
経路の距離を求める
import random
BACKGROUND_COLOR = color(0, 44, 77)
SIZE = 1000
STEP = 200
# 都市の座標リスト
cities = [
(23, 1),
(39, 1),
(21, 3),
(23, 3),
# (25, 4),
# (27, 4),
(39, 3),
(41, 3),
# (25, 6),
# (27, 6),
(31, 12),
(41, 12),
(31, 14),
(37, 14),
(29, 16),
(37, 16),
(1, 16),
(3, 16),
(19, 16),
(21, 16),
(16, 18),
(19, 18),
(3, 20),
(5, 20),
(13, 20),
(16, 20),
(29, 20),
(33, 20),
(29, 22),
(31, 22),
(5, 22),
(7, 22),
(11, 22),
(13, 22),
(31, 24),
(33, 24),
(7, 24),
(11, 24),
(1, 28),
(3, 28),
(27, 29),
(29, 29),
(3, 30),
(5, 30),
(5, 32),
(7, 32),
(25, 32),
(27, 32),
(7, 34),
(9, 34),
(23, 34),
(25, 34),
(9, 36),
(11, 36),
(17, 36),
(19, 36),
(15, 38),
(17, 38),
(19, 38),
(21, 38),
(13, 40),
(15, 40),
(13, 42),
(15, 42),
(23, 42),
(25, 42),
(11, 44),
(15, 44),
(21, 44),
(25, 44)
]
city_num = len(cities)
def setup():
size(SIZE, SIZE)
def draw():
background(BACKGROUND_COLOR)
noFill()
for i in range(int(SIZE / STEP)):
stroke(0, 255, 0, 50)
line(-2000, i * STEP, 2000, i * STEP)
line(i * STEP, -2000, i * STEP, 2000)
for j in range(10):
stroke(0, 255, 0, 25)
line(-2000, i * STEP + j * STEP / 10.0, 2000, i * STEP + j * STEP / 10.0)
line(i * STEP + j * STEP / 10.0, -2000, i * STEP + j * STEP / 10.0, 2000)
# ルートを表示
route = Route()
route.display()
print(frameCount, route.distance)
# テキスト表示
fill(255)
textSize(20)
text('distance: ' + str(route.distance), 10, 30)
class Route:
def __init__(self, a=[]):
if len(a) == 0:
self.city_nums = random.sample(
list(range(city_num)),
city_num
)
else:
self.city_nums = a
self.distance = 0
self.distance_list = []
self.calc()
def display(self):
stroke(127)
beginShape()
for i in self.city_nums:
x = cities[i][0] * STEP / 10.0
y = cities[i][1] * STEP / 10.0
vertex(x, y)
ellipse(x, y, 4, 4)
text(str(i), x + 10, y)
endShape(CLOSE)
def calc(self):
self.distance_list = []
for i in range(city_num):
start_city_num = self.city_nums[i]
end_city_num = self.city_nums[(i + 1) % city_num]
x0 = cities[start_city_num][0]
y0 = cities[start_city_num][1]
x1 = cities[end_city_num][0]
y1 = cities[end_city_num][1]
distance = dist(x0, y0, x1, y1)
self.distance_list.append(distance)
self.distance = sum(self.distance_list)
巡回セールスマン問題を解くための準備として、経路の距離を求めるプログラムを考えます。上記のコードを実行すると、ランダムに作成した経路とその距離を表示します。(経路の中で、目にあたる部分(4番5番8番9番)は問題を単純にするため省きました。ここから66都市で進めていきます。)
たくさんの経路を計算する必要があるので、Routeクラスを作成します。クラスを作成すると、同じような処理を繰り返すときにプログラムを見通しよく書くことができます。また機能の追加や修正するのに便利です。
Routeクラスの説明をします。
インスタンス変数city_nums を持ち、都市の経路を保存しています。インスタンス変数distance は経路の距離を、インスタンス変数distance_list は頂点間の距離をリストとして保存しています。
dispalyメソッドは、都市の位置と経路を表示することができます。calcメソッドは、インスタンス変数distance, distance_list を計算して保存する処理を実行します。
ランダムな経路を作成する
import random
BACKGROUND_COLOR = color(0, 44, 77)
SIZE = 1000
STEP = 200
# 都市の座標リスト
cities = [
(23, 1),
(39, 1),
(21, 3),
(23, 3),
# (25, 4),
# (27, 4),
(39, 3),
(41, 3),
# (25, 6),
# (27, 6),
(31, 12),
(41, 12),
(31, 14),
(37, 14),
(29, 16),
(37, 16),
(1, 16),
(3, 16),
(19, 16),
(21, 16),
(16, 18),
(19, 18),
(3, 20),
(5, 20),
(13, 20),
(16, 20),
(29, 20),
(33, 20),
(29, 22),
(31, 22),
(5, 22),
(7, 22),
(11, 22),
(13, 22),
(31, 24),
(33, 24),
(7, 24),
(11, 24),
(1, 28),
(3, 28),
(27, 29),
(29, 29),
(3, 30),
(5, 30),
(5, 32),
(7, 32),
(25, 32),
(27, 32),
(7, 34),
(9, 34),
(23, 34),
(25, 34),
(9, 36),
(11, 36),
(17, 36),
(19, 36),
(15, 38),
(17, 38),
(19, 38),
(21, 38),
(13, 40),
(15, 40),
(13, 42),
(15, 42),
(23, 42),
(25, 42),
(11, 44),
(15, 44),
(21, 44),
(25, 44)
]
city_num = len(cities)
random_update = 0
def setup():
global best_route, shortest_distance
size(SIZE, SIZE)
# 初期ルート
best_route = Route()
shortest_distance = best_route.distance
def draw():
global best_route, shortest_distance, random_update
background(BACKGROUND_COLOR)
noFill()
for i in range(int(SIZE / STEP)):
stroke(0, 255, 0, 50)
line(-2000, i * STEP, 2000, i * STEP)
line(i * STEP, -2000, i * STEP, 2000)
for j in range(10):
stroke(0, 255, 0, 25)
line(-2000, i * STEP + j * STEP / 10.0, 2000, i * STEP + j * STEP / 10.0)
line(i * STEP + j * STEP / 10.0, -2000, i * STEP + j * STEP / 10.0, 2000)
# ルートを表示
best_route.display()
# 新しいルートをランダムに作成
for _ in range(5):
new_route = Route()
if new_route.distance < best_route.distance:
best_route = new_route
shortest_distance = new_route.distance
random_update += 1
# テキスト表示
fill(255)
textSize(20)
text('number of trials: ' + str(frameCount), 10, 30)
text('shortest distance: ' + str(shortest_distance), 10, 60)
text('random update: ' + str(random_update), 10, 90)
class Route:
def __init__(self, a=[]):
if len(a) == 0:
self.city_nums = random.sample(
list(range(city_num)),
city_num
)
else:
self.city_nums = a
self.calc()
def display(self):
stroke(127)
beginShape()
for i in self.city_nums:
x = cities[i][0] * STEP / 10.0
y = cities[i][1] * STEP / 10.0
vertex(x, y)
ellipse(x, y, 4, 4)
text(str(i), x + 10, y)
endShape(CLOSE)
def calc(self):
self.distance_list = []
for i in range(city_num):
start_city_num = self.city_nums[i]
end_city_num = self.city_nums[(i + 1) % city_num]
x0 = cities[start_city_num][0]
y0 = cities[start_city_num][1]
x1 = cities[end_city_num][0]
y1 = cities[end_city_num][1]
distance = dist(x0, y0, x1, y1)
self.distance_list.append(distance)
self.distance = sum(self.distance_list)
巡回セールスマン問題を通常の方法で解いてみます。すべての経路を数え上げて計算することは不可能(時間的に)であることから、ランダムに経路を作成して、ベストルートよりも経路が短いときに、ベストルートを更新することにします。
1000回試行した結果をアニメーションにしてみました。経路を9回アップデートしましたが、まだまだ最短ルートには程遠い結果になりました。
もっと別のアプローチが必要のようです。
別のアプローチ
前の説ではランダムな経路を作成して、ベストルートを更新していく方法を考えました。ランダムな経路で更新するのは効率が悪いことは結果からも示されました。
次の方針として、ベストルートを一部変更したものと、ベストルートを比べて経路が短くなればベストルートを更新することにします。
文章が長くなりましたので、次回「遺伝的アルゴリズム(後編)」に続きます。いよいよ生物進化のシミュレーションが登場します。お楽しみに!
前の記事
Processing でグラフを描く⑰ らせん
次の記事
Processing でグラフを描く⑲ 遺伝的アルゴリズム(後編)
その他のタイトルはこちら
