見出し画像

Processing でグラフを描く⑰　らせん

creativival

Processing でグラフを描く　第１７回目です。

らせんにはたくさんの種類があることをご存じでしょうか。わたしも今回、らせんのことを調べて、多くの種類のらせんがあることを知りました。らせんを定義する式により、らせんの形状は変化します。らせんを使ったジェネラティブアートに挑戦します。

まずはフィボナッチ数列の話から始めます。

フィボナッチ数列

$$
F_0 = 0\\
F_1 = 1\\
F_{n+2} = F_{n+1} + F_{n}\\
$$

上記の漸化式で定義される数列をフィボナッチ数列と呼びます。実際に初めのいくつかを書き出すと、0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987… となり、数列は無限に続いていきます。

この一見ランダムな数の並びが注目されたのは、自然界の現象にフィボナッチ数列が現れるからです。たとえばウサギの繁殖であったり、植物の枝分かれや動物の血管の枝分かれなどにフィボナッチ数列が現れます。花びらの枚数やヒマワリの種の並びなどもフィボナッチ数列に従っています。自然は数を数えながら創造物を作っているのでしょうか。不思議です。

フィボナッチらせん

def fibonacci(n):
    if n == 0:
        fibonacci_nums = [0]
    else:
        fibonacci_nums = [0, 1]
        for i in range(n - 1):
            fibonacci_nums.append(
                fibonacci_nums[i] + fibonacci_nums[i + 1]
            )
    return fibonacci_nums


SIZE = 1200  # 画面サイズ
rect_num = 16
fibonacci_nums = fibonacci(rect_num)
scale = 8
color_scale = 100.0 / rect_num


def setup():
    size(SIZE, SIZE)
    frameRate(5)
    colorMode(HSB, 100)


def draw():
    background(100)
    pushMatrix()
    translate(width / 2, height / 2)
    x = 0
    y = 0
    count = min(frameCount - 1, rect_num)
    for i in range(count):
        fill(color_scale * i, 100, 100)
        # noFill()
        num = fibonacci_nums[i] * scale
        if i % 4 == 0:
            x += num
            y += num
            noStroke()
            rect(x - num, y - num, num, num)
            noFill()
            stroke(0)
            arc(x - num, y, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        elif i % 4 == 1:
            x -= num
            y += num
            noStroke()
            rect(x, y - num, num, num)
            noFill()
            stroke(0)
            arc(x, y - num, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        elif i % 4 == 2:
            x -= num
            y -= num
            noStroke()
            rect(x, y, num, num)
            noFill()
            stroke(0)
            arc(x + num, y, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        else:
            x += num
            y -= num
            noStroke()
            rect(x - num, y, num, num)
            noFill()
            stroke(0)
            arc(x, y + num, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
    popMatrix()
fibonacci

フィボナッチ数列の値で正方形を作り、それをらせん状に並べます。正方形の対角の頂点を円弧でつなぐと、らせんが現れます。これがフィボナッチらせんです。

この美しい曲線は巻き貝の構造をよく近似しています。「フィボナッチ　貝」で画像検索すると、ステキな画像がたくさん出てきます。フィボナッチ数列との関係に驚くことでしょう。

らせんを並べてみる

def fibonacci(n):
    if n == 0:
        fibonacci_nums = [0]
    else:
        fibonacci_nums = [0, 1]
        for i in range(n - 1):
            fibonacci_nums.append(
                fibonacci_nums[i] + fibonacci_nums[i + 1]
            )
    return fibonacci_nums


def archimedes(angle, a, phase=0.0):
    r = a * angle
    return r * cos(angle + phase), r * sin(angle + phase)


def fermat(angle, a, phase=0.0):
    r = a * sqrt(angle)
    return r * cos(angle + phase), r * sin(angle + phase)


def logarithm(angle, a, phase=0.0):
    r = pow(a, angle)
    return r * cos(angle + phase), r * sin(angle + phase)


HAS_SAVED_FRAMES = True  # default: False
SIZE = 1000  # 画面サイズ
rect_num = 16
fibonacci_nums = fibonacci(rect_num)
scale = 8
points_list = []


def setup():
    size(SIZE, SIZE)
    frameRate(60)
    strokeWeight(2)
    # グラフのデータ
    points_list.append(
        [archimedes(radians(i), 5, HALF_PI) for i in range(10000)],
    )
    points_list.append(
        [fermat(radians(i), 20, HALF_PI) for i in range(10000)],
    )
    points_list.append(
        [logarithm(radians(i), 1.2, HALF_PI) for i in range(10000)],
    )


def draw():
    background(255)
    pushMatrix()
    translate(width / 2, height / 2)
    x = 0
    y = 0
    for i in range(rect_num):
        # フィボナッチらせん
        noFill()
        num = fibonacci_nums[i] * scale
        if i % 4 == 0:
            x += num
            y += num
            stroke(127)
            rect(x - num, y - num, num, num)
            stroke(0)
            arc(x - num, y, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        elif i % 4 == 1:
            x -= num
            y += num
            stroke(127)
            rect(x, y - num, num, num)
            noFill()
            stroke(0)
            arc(x, y - num, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        elif i % 4 == 2:
            x -= num
            y -= num
            stroke(127)
            rect(x, y, num, num)
            noFill()
            stroke(0)
            arc(x + num, y, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)
        else:
            x += num
            y -= num
            stroke(127)
            rect(x - num, y, num, num)
            noFill()
            stroke(0)
            arc(x, y + num, num * 2, num * 2, (3 + i) * HALF_PI, (4 + i) * HALF_PI)

    theta = min(frameCount - 1, len(points_list[0]) - 1)
    for i in range(theta):
        # アルキメデスらせん
        points = points_list[0]
        x0, y0 = points[i]
        x1, y1 = points[i + 1]
        stroke(255, 0, 0)
        line(x0, y0, x1, y1)
        # フェルマーらせん
        points = points_list[1]
        x0, y0 = points[i]
        x1, y1 = points[i + 1]
        stroke(0, 255, 0)
        line(x0, y0, x1, y1)
        # 対数らせん
        points = points_list[2]
        x0, y0 = points[i]
        x1, y1 = points[i + 1]
        stroke(0, 0, 255)
        line(x0, y0, x1, y1)
    popMatrix()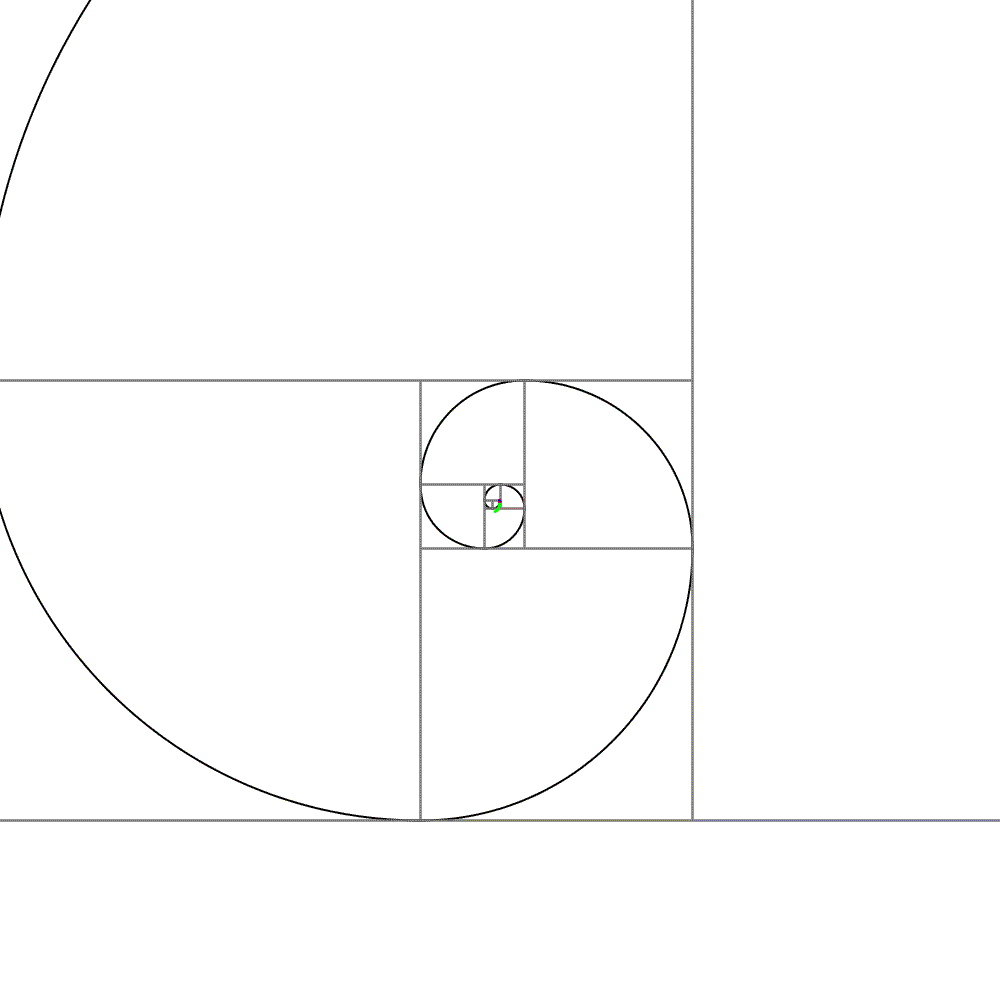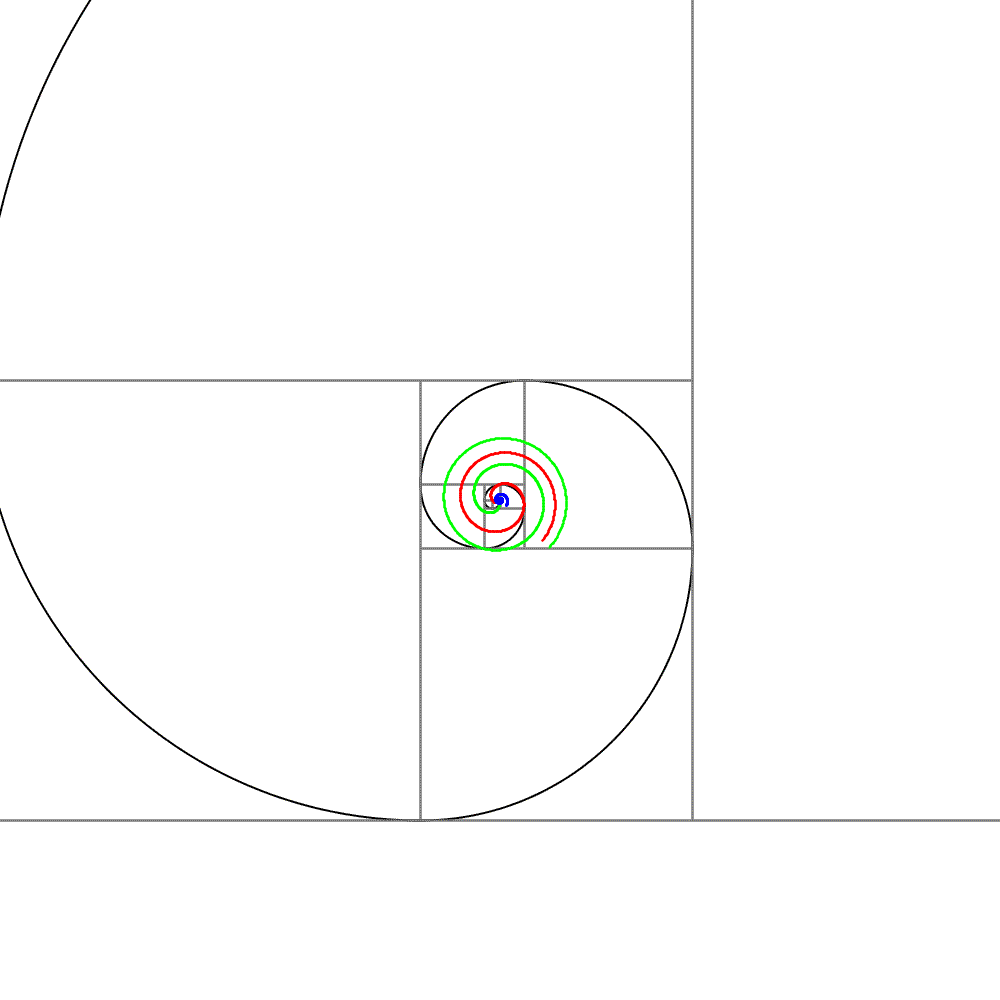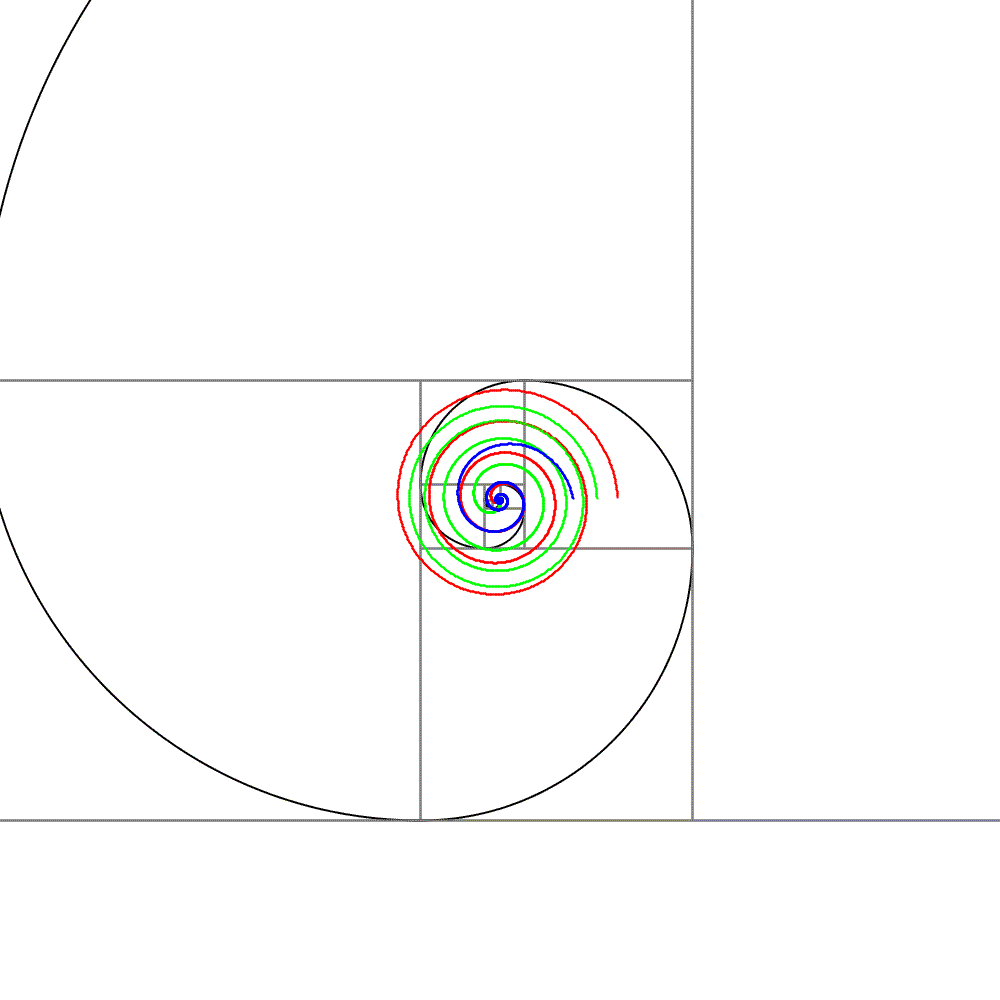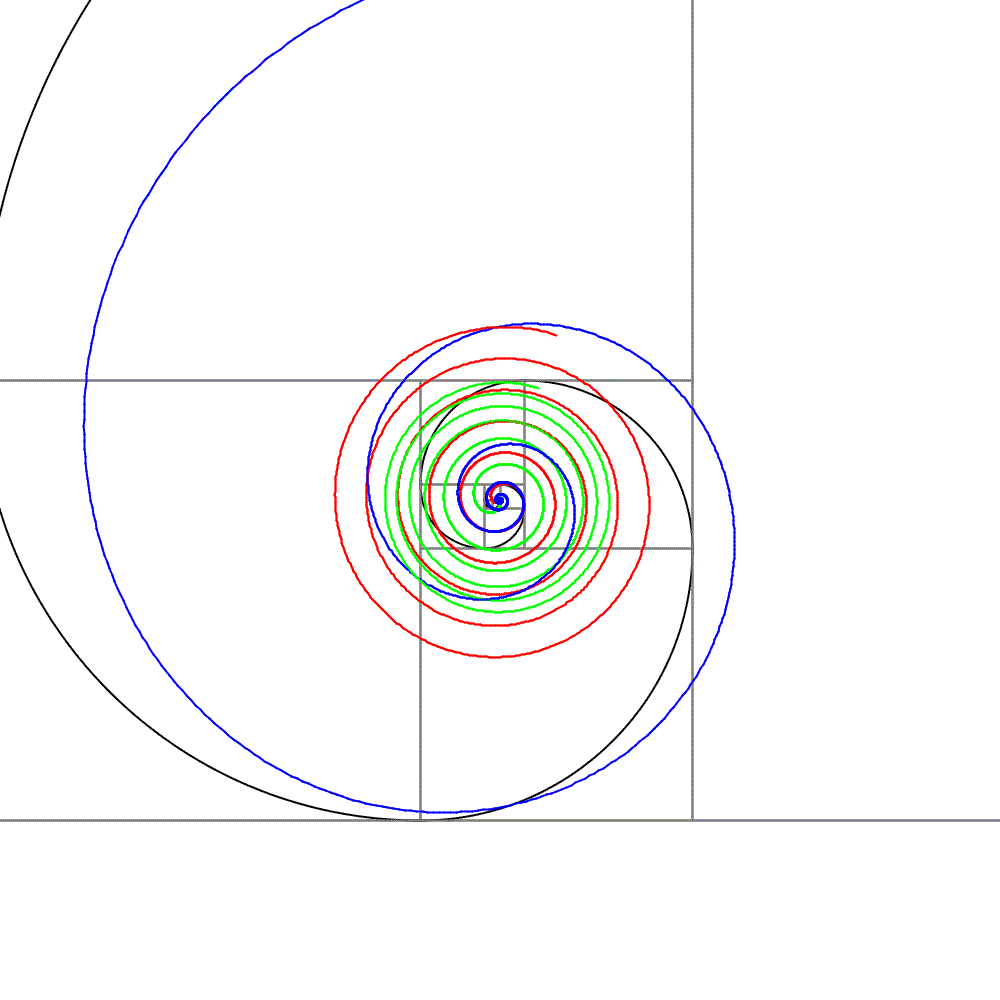
spirals

４本のらせんを同時に描きました。

赤のアルキメデスらせんは「極座標」の回で詳しく説明しました。$${r = a \theta}$$ で表される曲線で、一番見慣れた形状をしています。

緑のフェルマーらせんは $${r = a \sqrt{\theta}}$$ で表される曲線です。赤と比べると、らせんの変化率が小さいことがわかります。

青の対数らせんは $${r = a^{\theta}   (a > 1)}$$ で表される曲線です。一番変化率が大きく、初めは変化が見られませんが、急に大きくなり、赤と緑を追い抜いていきます。

次は対数らせんを使ったジェネラティブアートを作成します。

対数らせん

def logarithm(angle, a, phase=0.0):
    r = pow(a, angle)
    return r * cos(angle + phase), r * sin(angle + phase)


SIZE = 800  # 画面サイズ
points_list = []
line_num = 24


def setup():
    size(SIZE, SIZE)
    frameRate(60)
    colorMode(HSB, 100)
    # グラフのデータ
    for j in range(line_num):
        points_list.append(
            [logarithm(radians(i), sqrt(2), j * TWO_PI / line_num) for i in range(2000)],
        )


def draw():
    background(0)
    pushMatrix()
    translate(width / 2, height / 2)
    theta = min(frameCount - 1, len(points_list[0]) - 1)
    for j in range(line_num):
        points = points_list[j]
        stroke(j * 100.0 / line_num, 100, 100)
        for i in range(theta):
            # 対数らせん
            x0, y0 = points[i]
            x1, y1 = points[i + 1]
            line(x0, y0, x1, y1)
    popMatrix()
logarithm

対数らせんを２４本並べてアニメーションにしました。らせんの本数はもっと増やしても面白そうです。この画像は $${r = a^{\theta}   (a ＝\sqrt{2})}$$ で作成しましたが、a の値を変えると、らせんの広がり方が変わっていきます。  a を大きくしたり、小さくしたりして遊んでみてください。

フェルマーらせん

def fermat(angle, a, phase=0.0):
    r = a * sqrt(angle)
    return r * cos(angle + phase), r * sin(angle + phase)


HAS_SAVED_FRAMES = True  # default: False
SIZE = 800  # 画面サイズ
points_list = []
ratio = 17.0 / 55
scale = 0.5
# scale = 0.2


def setup():
    size(SIZE, SIZE)
    frameRate(60)
    colorMode(HSB, 100)
    strokeWeight(2)
    # グラフのデータ
    points_list.append(
        [fermat(TWO_PI * ratio * i, sqrt(i), HALF_PI) for i in range(5000)],
    )


def draw():
    background(0)
    pushMatrix()
    translate(width / 2, height / 2)
    # 離散的ならせん
    theta = min(frameCount - 1, len(points_list[0]) - 1)
    points = points_list[0]
    stroke(100, 100, 100)
    for i in range(theta):
        x0, y0 = points[i]
        ellipse(x0 * scale, y0 * scale, 1, 1)
    popMatrix()
    print(frameCount)
fermat scale=0.5
fermat scale=0.２

フェルマーらせん $${r = \sqrt{\theta}}$$ を角度 $${2 \pi \times \frac{17}{55}}$$ ずつプロットしたアニメーションです。初めは右回りのらせんが、次に左回りに変わり、最後直線に伸びていくように見えます。実は、これは目の錯覚で、ずっと右回りのらせんなのです。面白いですね。

今回はらせんを使って遊んでみました。上記のコードは Processing (Pythonモード)に貼り付けると動きますので、興味のある方はご自分のパソコンで試してみてください。

前の記事
Processing でグラフを描く⑯　ハーモノグラフ
次の記事
Processing でグラフを描く⑱　遺伝的アルゴリズム（前編）

その他のタイトルはこちら


この記事が気に入ったらサポートをしてみませんか？