
ARプログラミング入門 ③球体を作る
Voxelamming(ボクセラミング)の世界では、直方体のボクセルを組み合わせて様々な形を作ることができます。家、車、動物… アイデア次第で、Voxelammingではたくさんのものを作れます。
しかし、球体や円錐のような、滑らかな曲線で構成された形を作ることは難しいと感じたのではないでしょうか?
Voxelammingでは、直方体のボクセルしか配置できませんが、今回の記事で紹介する条件分岐という考え方を使うことで、球体のような複雑な形状も表現できるようになります。
まるで粘土をこねて形を作るように、Voxelammingで自由自在に形を作れるようになりましょう!
読み始める前に
この記事では、私たちが開発した無料ARプログラミング学習アプリ「Voxelamming(ボクセラミング)」の使い方を、Pythonを使ったサンプルコードと共に詳しく解説していきます。
iPhone/iPad/Vision Proをお持ちの方は、App StoreからVoxelammingアプリをダウンロードして、ぜひ一緒にプログラミングに挑戦してみましょう!
この記事は、連載第1回目の内容を理解し、Pythonのインストール、voxelammingパッケージのインストール、そしてVS Code(または別のIDE)の設定が完了していることを前提としています。
前回の復習と今回の目標
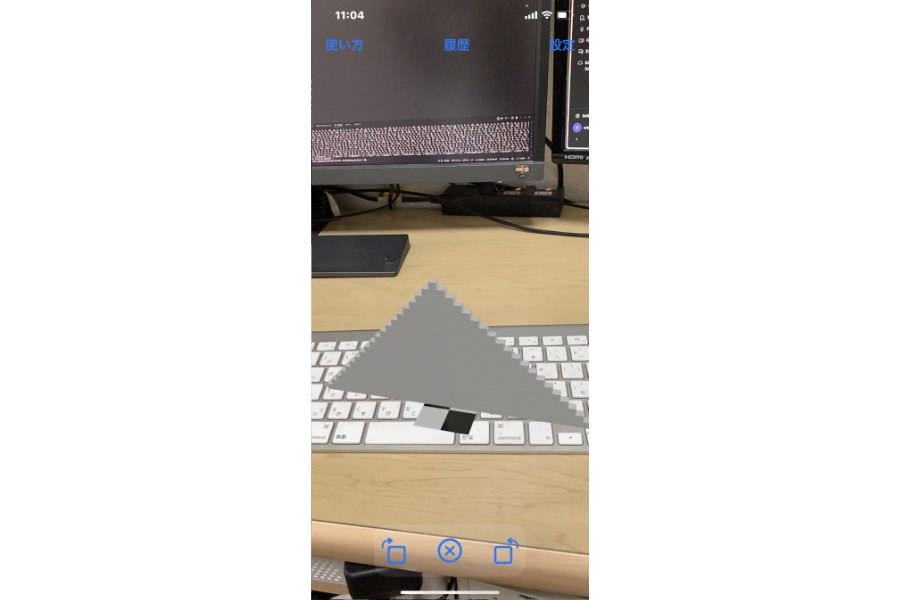
前回は、複数の for 文を組み合わせることで、階段状のピラミッドのような立体的な構造物も作れることを学びました。
しかし、階段状のピラミッドは、あくまで直方体を積み重ねたものであり、滑らかな曲面を持つ球体のような形を作ることはできません。
そこで今回は、条件分岐を活用して、Voxelammingで球体を作成することを目標にします。
条件分岐をマスターすれば、Voxelammingで表現できる形の幅が大きく広がります。
それでは、早速始めていきましょう!
今回使うPythonの知識
if文:条件分岐でプログラムを賢く制御する
今回のサンプルコードでは、if文という構文を使って、条件分岐を行います。
条件分岐とは、ある条件が満たされているかどうかによって、プログラムの動作を変えることです。
例えば、変数 num に入っている数値が偶数かどうかを判定し、偶数なら「偶数です」、奇数なら「奇数です」と表示するプログラムは、if文を使って以下のように記述することができます。
num = 6
if num % 2 == 0: # もし num を 2 で割った余りが 0 なら(偶数なら)
print("偶数です")
else: # そうでなければ(奇数なら)
print("奇数です")if文の基本的な構造は次のとおりです。
if 条件式:
条件式が真(True)の場合に実行される処理条件式: 真(True)または偽(False)のどちらかの値になる式を記述します。
条件式が真(True)の場合に実行される処理: 条件式が真(True)だった場合にのみ実行される処理を記述します。
else文:条件式が偽(False)の場合の処理
if文には、else文を組み合わせることで、条件式が偽(False)だった場合に実行する処理を記述することができます。
if 条件式:
条件式が真(True)の場合に実行される処理
else:
条件式が偽(False)の場合に実行される処理先ほどの偶数・奇数の判定の例では、if文で偶数の場合の処理を記述し、else文で奇数の場合の処理を記述しています。
elif文:複数の条件分岐
さらに、elif文を使うことで、複数の条件分岐を記述することができます。
if 条件式1:
条件式1が真(True)の場合に実行される処理
elif 条件式2:
条件式2が真(True)の場合に実行される処理
else:
いずれの条件式も偽(False)の場合に実行される処理例えば、点数によって成績を判定するプログラムを書きたい場合は、以下のように記述することができます。
score = 75
if score >= 90: # もし score が 90 以上なら
print("成績はAです")
elif score >= 80: # そうでなく、score が 80 以上なら
print("成績はBです")
elif score >= 70: # そうでなく、score が 70 以上なら
print("成績はCです")
else: # そうでなければ
print("成績はDです")if文、elif文、else文を組み合わせることで、複雑な条件分岐を表現することができます。
比較演算子
条件式には、比較演算子を使って、値の比較を行うことができます。
| 演算子 | 意味 |
| :----: | :----: |
| == | 等しい |
| != | 等しくない |
| < | より小さい |
| <= | 以下 |
| > | より大きい |
| >= | 以上 |論理演算子
複数の条件式を組み合わせたい場合は、論理演算子を使うことができます。
| 演算子 | 意味 |
| :----: | :----: |
| and | かつ |
| or | または |
| not | 否定 |算術演算子
Pythonでは、数値を計算するための算術演算子が用意されています。
| 演算子 | 意味 | 例 | 結果 |
| :----: | :-----------: | :----: | :----: |
| + | 加算 | 10 + 5 | 15 |
| - | 減算 | 10 - 5 | 5 |
| * | 乗算 | 10 \* 5 | 50 |
| / | 除算 | 10 / 5 | 2 |
| // | 切り捨て除算 | 10 // 3 | 3 |
| % | 剰余 | 10 % 3 | 1 |
| ** | べき乗 | 10 \*\* 2 | 100 |切り捨て除算(//)は、計算結果の小数点以下を切り捨てた整数値を返します。
剰余(%)は、割り算の余りを返します。
べき乗(**)は、左辺の値を右辺の値で累乗した結果を返します。
まとめ
今回は、条件分岐を行うための if 文について詳しく解説しました。if 文を使うと、コンピューターに自動で「成績振り分け」のような仕事をさせることができるようになります。if 文は、プログラミングにおいて非常に重要な概念です。
算術演算子は、学校の算数・数学で学ぶ計算式を作ることができます。プログラミング、特に3Dアプリケーションでは算術演算子を多用するので、全ての演算子(+, -, *, / など)を覚えるようにしましょう。
次の章では、いよいよサンプルコードを見ていきましょう!
サンプルコード解説
球体を作る
今回のサンプルコードでは、条件分岐を使って、Voxelammingで球体を作ります。VS Codeで「sphere.py」という名前のPythonファイルを作成して、次のコードを記述してください。
# voxelammingパッケージからVoxelammingクラスをインポートします
from voxelamming import Voxelamming
# 球体の半径を設定する
radius = 11
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
# ボクセルの設定を行います
vox.set_box_size(0.5)
vox.set_build_interval(0.01)
# ボクセルを配置するため、位置と色を設定します
for i in range(-radius, radius + 1):
for j in range(-radius, radius + 1):
for k in range(-radius, radius + 1):
if (radius - 1) ** 2 <= i ** 2 + j ** 2 + k ** 2 < radius ** 2:
print(i, j, k)
vox.create_box(i, j, k, 0, 1, 1)
# ボクセルデータをアプリに送信します。
vox.send_data("square")上記のコードは、Voxelammingパッケージのバージョン0.3.0以降で有効です。それ以前のバージョンをインストール済みの方は「pip install --upgrade voxelamming」コマンドでアップデートを行なってください。
コード解説 パート1:準備
最初の数行を見てみましょう。
from voxelamming import Voxelamming
# 球体の半径を設定する
radius = 11
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
# ボクセルの設定を行います
vox.set_box_size(0.5)
vox.set_build_interval(0.01)1行目は、voxelammingパッケージからVoxelammingクラスをインポートしています。
3行目は、これから作成する球体の半径を指定する変数 radius を定義し、11 を代入しています。
5行目は、Voxelammingアプリに表示されているルーム名を変数 room_name に代入しています。このルーム名は、アプリとの直接の接続を可能にするために、アプリ起動画面に表示されている文字に入れ替えるようにします。(数値ではなく、文字列であることに注意!)
7行目は、Voxelammingクラスのインスタンスを生成し、変数voxに代入しています。
9行目と10行目は、ボクセルのサイズと配置間隔を設定しています。
コード解説 パート2:球体の作成
次に、球体を作成する部分を見ていきましょう。球体の中にボクセルを配置すると、ボクセルの個数が多くなり、アプリが止まったり、異常終了することがあります。そこで、ボクセルの個数が少なくなるように、表面だけボクセルを配置して、中身は空の球体を作成します。
for i in range(-radius, radius + 1):
for j in range(-radius, radius + 1):
for k in range(-radius, radius + 1):
if (radius - 1) ** 2 <= i ** 2 + j ** 2 + k ** 2 < radius ** 2:
print(i, j, k)
vox.create_box(i, j, k, 0, 1, 1)このコードでは、3重の for 文を使って、辺の長さ「radius x 2」の立方体の内部を、ボクセル1つ分の幅で走査(すべて調べ上げること)しています。
if 文を理解するには、球体を表す数式を理解する必要があります。
球の中心座標を(0, 0, 0)としたとき、球体の表面上の点は、次の式を満たします。この式の x, y, z は3次元空間上の座標を表しています。r は球体の半径です。
$${x^2 + y^2 + z^2 = r^2}$$
この式を満たす座標(x, y, z)にボクセルを配置すれば、半径 r の球体を作ることができます。
そこで、サンプルコードでは、次の条件式を使って、球体の表面付近にある座標を判定しています。
if (radius - 1) ** 2 <= i ** 2 + j ** 2 + k ** 2 < radius ** 2:この条件式は、座標(i, j, k)が、半径(radius - 1)の球面と半径radiusの球面の間にあるかどうかを判定しています。
(radius - 1) ** 2 : 半径 (radius - 1) の球面の半径の2乗
i ** 2 + j ** 2 + k ** 2 : 座標 (i, j, k) と原点(0, 0, 0)との距離の2乗
radius ** 2: 半径 radius の球面の半径の2乗
この条件式を満たす座標にボクセルを配置することで、球体に近い形を作ることができます。
vox.create_box(i, j, k, 0, 1, 1) : 座標(i, j, k)の位置に、シアン色のボクセル(r=0, g=1, b=1)を配置します。
コード解説 パート3:ボクセルデータの送信
最後に、以下のコードで作成したボクセルデータをVoxelammingアプリに送信します。
vox.send_data("square")この章では、条件分岐と3重のfor文を使って、球体を作成するコードを解説しました。
このコードは条件式で、球体の表面近くのボクセルだけを配置しています。このことは、配置するボクセルの数を大幅に減らすことで、Voxelammingアプリの動作を安定させる効果があります。
使用するデバイスの性能にもよりますが、数千個以上のボクセルを配置するときは、ボクセル数を減らせないか、プログラム上で工夫することを勧めます。
サンプルコードを実行する
それでは、いよいよサンプルコードを実行して、AR空間に球体を出現させてみましょう!
1. ルーム名を確認
まず、Voxelammingアプリを起動し、画面中央に表示されているルーム名を確認してください。
2. ルーム名をコードに反映
サンプルコードの room_name 変数の値を、アプリに表示されているルーム名に書き換えます。書き換え後、保存するのを忘れないようにしてください。
room_name = "XXXX" # XXXXをアプリのルーム名に書き換える3. コードを実行
VS Codeでターミナルを開き、次のコマンドを実行します。
ターミナルからコマンドを実行する
python sphere.py
上記コードを実行すると、プログラムが正常に実行されると、Voxelammingアプリ上に、シアン色の球体が出現します! サンプルコードのradiusの値を変えると、もっと大きな球体を描くことができます。挑戦してみましょう!
実行できないときは
もし、うまく線が描画されない場合は、以下の点を確認してみてください。
Voxelammingアプリとパソコンが同じWi-Fiネットワークに接続されているか
サンプルコードの room_name 変数の値が、アプリに表示されているルーム名と一致しているか
回線が混み合っている場合は、時間をおいてから再度、コマンドを実行してください。
次の章では、応用として、今回作成した球体を改造して、オリジナル作品作りに挑戦してみましょう!
応用:オリジナル作品作りに挑戦!
問題1: 円錐を作ってみよう!
球体を作ることができたあなたは、もうVoxelammingマスターへの道を着実に進んでいます!
次は、球体で学んだ条件分岐のテクニックを応用して、円錐を作成してみましょう。
Voxelammingでは、真円のコーンを作ることは難しいですが、台形を積み重ねることで、円錐に近い形を作ることができます。
挑戦する前に
自分で考えてコードを書いてみると、プログラミングの理解がより深まります。時間がない方は、回答例を参考にしてください。
回答例
VS Codeで「corn.py」という名前のファイルを作成し、以下のコードを記述してください。
from voxelamming import Voxelamming
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
# ボクセルの設定を行います
vox.set_box_size(0.5)
vox.set_build_interval(0.01)
# 円錐の高さ
height = 15
# 各段の幅を計算
for i in range(height):
radius = height - i + 5 # i段目の半径
for j in range(-radius, radius + 1):
for k in range(-radius, radius + 1):
# 台形を作る条件
if (radius - 1) ** 2 <= j ** 2 + k ** 2 < radius ** 2:
vox.create_box(j, i, k, 1, 0, 0) # 赤色でボクセルを配置
# ボクセルデータをアプリに送信します。
vox.send_data("cone")解説
このプログラムでは、円錐の高さを height という変数で定義し、for 文を使って一段ずつボクセルを積み上げて円錐を作成しています。
外側の for i in range(height) は、円錐の高さを height に設定し、その高さまでボクセルを積み上げるためのループです。
内側の2つの for 文は、各段におけるx座標とz座標を指定し、ボクセルを配置する範囲を定めています。
if (radius - 1) ** 2 <= j**2 + k**2 < radius**2: の条件式は、各段のボクセルを配置する範囲を円形に制限するために使用されます。この条件式は、x軸とz軸で形成される平面における円の式を表しています。
radius = height - i + 5 で、各段の半径を計算しています。「+ 5」とすることで、台形の円錐を実現しています。
このプログラムを実行すると、AR空間に赤い円錐が出現します。
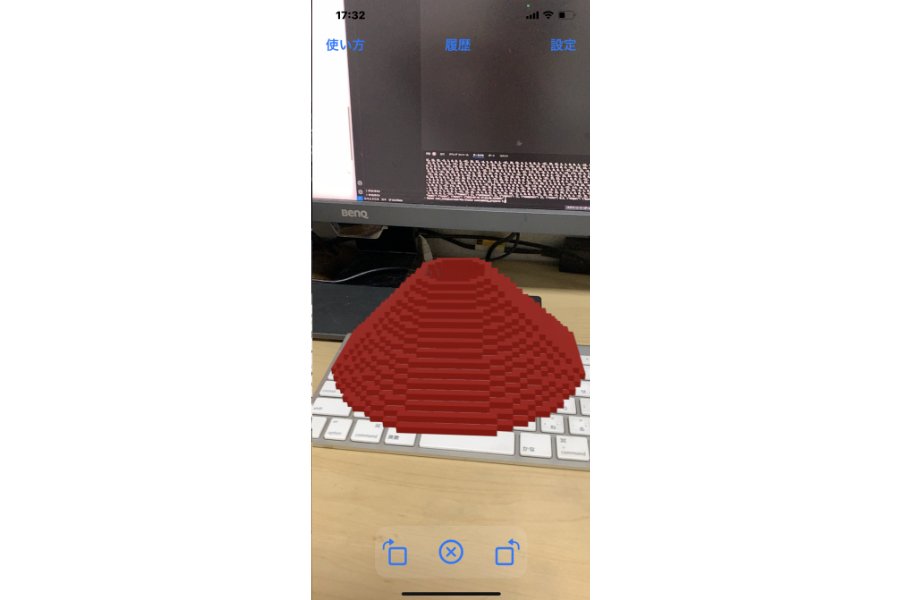
挑戦してみよう!
円錐の色や大きさを変えてみよう。
複数の円錐を組み合わせて、面白い形を作ってみよう。
条件分岐を使いこなせば、Voxelammingで表現できる世界は無限に広がります! ぜひ、色々な形に挑戦して、あなただけのARアート作品を生み出してください!
問題2: ドーナツを作ってみよう!
Voxelammingを使って、今度はドーナツの形を作ってみましょう!
ドーナツは、円を回転させてできる立体なので、円の方程式と条件分岐を組み合わせることで表現できます。
挑戦する前に
自分で考えてコードを書いてみると、プログラミングの理解がより深まります。時間がない方は、回答例を参考にしてください。
回答例
VS Codeで「donut.py」という名前のファイルを作成し、以下のコードを記述してください。
from math import sqrt
# voxelammingパッケージからVoxelammingクラスをインポートします
from voxelamming import Voxelamming
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
# ボクセルの設定を行います
vox.set_box_size(0.5)
vox.set_build_interval(0.01)
# ドーナツの大きな円の半径
donut_outside_radius = 16
# ドーナツの小さな円の半径
donut_inside_radius = 8
# ドーナツの半径は、大きな円の半径と小さな円の半径の平均
donut_center_radius = (donut_outside_radius + donut_inside_radius) / 2
# ドーナツの断面の円の半径は、大きな円の半径と小さな円の半径の差の半分
donut_cross_section_radius = (donut_outside_radius - donut_inside_radius) / 2
# 上半分のみボクセルを配置(ボクセルの数を減らすため)
for i in range(0, donut_outside_radius + 1):
# Y軸方向にドーナツの断面の円の半径の範囲内の場合
if -donut_cross_section_radius <= i <= donut_cross_section_radius:
# 2つの円に挟まれた部分にボクセルを配置
# 大きな円とドーナツの半径の差、小さな円とドーナツの半径の差
delta_radius = sqrt(donut_cross_section_radius ** 2 - i ** 2)
# 大きな円の半径
big_radius = int(donut_center_radius + delta_radius)
# 小さな円の半径
small_radius = int(donut_center_radius - delta_radius)
print(big_radius, small_radius)
for j in range(-big_radius, big_radius + 1):
for k in range(-big_radius, big_radius + 1):
# 円の式を使って、ドーナツの形になる条件を指定
if small_radius ** 2 <= j ** 2 + k ** 2 < big_radius ** 2:
vox.create_box(j, i, k, 1, 0, 1) # 紫色でボクセルを配置
# ボクセルデータをアプリに送信します。
vox.send_data("donut")解説
このプログラムでは、ドーナツを構成する2つの円(大きな円と小さな円)の半径をそれぞれ donut_outside_radius と donut_inside_radius という変数で定義しています。
この2つの変数から計算される変数がたくさん出てきますが、図にして整理してみます。プログラムに書かれた変数(donut_center_radiusなど)がどの値を示しているかを確認しておきましょう。

そして、3重の for 文を用いて、大きな円の半径を基準とした立方体の内部を走査し、ドーナツ内部にボクセルを配置しています。複雑な形状を生成するために、いくつかの工夫が凝らされています。for文の部分を詳しく解説します。
for i in range(0, donut_outside_radius + 1): : y座標を 0 から donut_outside_radius まで変化させながらループを回します。ドーナツは上下対称な形なので、計算量を減らすために上半分だけを生成しています。
if -donut_cross_section_radius <= i <= donut_cross_section_radius: : y座標がドーナツの断面の円の半径の範囲内かどうかを判定しています。この条件式を満たすy座標の範囲だけが、ドーナツの断面と重なる部分です。
delta_radius = sqrt(donut_cross_section_radius**2 - i**2) : 断面の円における、y座標 i に対応するx座標の絶対値を計算しています。三平方の定理から導かれます。sqrt(引数)は、引数の数値の平方根を返します。
big_radius = int(donut_center_radius + delta_radius) : y座標 i におけるドーナツの外側の円の半径を計算しています。
small_radius = int(donut_center_radius - delta_radius): y座標 i におけるドーナツの内側の円の半径を計算しています。
for j in range(-big_radius, big_radius + 1):: x座標を -big_radius から big_radius まで変化させながらループを回します。
for k in range(-big_radius, big_radius + 1): : z座標を -big_radius から big_radius まで変化させながらループを回します。
if small_radius**2 <= j**2 + k**2 < big_radius**2: : 座標 (j, k) が、内側の円と外側の円の間に存在するかどうかを判定しています。
vox.create_box(j, i, k, 1, 0, 1): 条件を満たす座標に、紫色のボクセルを配置します。
実行結果

このプログラムを実行すると、AR空間に紫色のドーナツが出現します!
ドーナツの穴の大きさや太さは、big_radius と small_radius の値を変更することで調整できます。ぜひ色々試してみてください。
まとめ
今回は、条件分岐という新しいプログラミングの技を習得し、Voxelammingで球体やドーナツのような複雑な形状を作成する方法を学びました。
if 文を使って、条件に応じてボクセルの色や配置を変えることができるようになりました。
球体やドーナツを作る際に、数学的な考え方とプログラミングを組み合わせることで、Voxelammingの可能性が大きく広がることを実感できたのではないでしょうか。
Voxelammingは、自由な発想を形にすることができる、創造力を刺激するツールです。
条件分岐をマスターしたあなたは、さらに複雑で美しいARアート作品を生み出すことができるはずです。
次の記事では、draw_line メソッドを使って、線で構成された立体図形を作成します。
Voxelammingで表現できる世界を、さらに広げていきましょう!
AR プログラミング入門シリーズ
ARプログラミング入門シリーズの一覧です。全8回で完結します。
次回、中級編は構想中です。ご期待ください!
第1回 Voxelammingについて
第2回 ボクセルアートの色と形を変えてみよう!
第3回 球体を作る
第4回 ランダムな線でアートを描こう!
第5回 アニメーションで命を吹き込もう!
第6回 タートルグラフィックスで図形を描こう!
第7回 文字でAR空間にメッセージを描こう!
第8回 再帰関数でフラクタルに挑戦!
サンプルコードを公開
GitHubレポジトリでサンプルコードを公開しています。記事を読むときに参照してください。
