
ARプログラミング入門 ⑧再帰関数でフラクタルに挑戦!
自然界には、雪の結晶や木の枝分かれ、海岸線など、複雑で美しい形をしたものがたくさんあります。
これらの形には、「フラクタル」と呼ばれる、不思議な法則が隠されていることがあります。
フラクタルとは、一部分が全体と自己相似になっている図形のことです。次の図は、Pythonのタートルグラフィックスで描いたフラクタル図形の例です。シェルピンスキーの三角形と呼ばれます。

Voxelamming(ボクセラミング)の世界でも、再帰関数と呼ばれるプログラミングのテクニックを使うことで、美しいフラクタル図形を表現することができます。
再帰関数は、まるで魔法のように、自分自身を呼び出すことで、複雑なパターンを簡単に生成することができます。
しかし、再帰関数とフラクタル図形は、少し難しい概念です。
頭を柔らかくして、じっくりと考えていく必要があるので、気合を入れて読み進めていきましょう!
今回は、再帰関数の仕組みを理解し、Voxelammingでフラクタル図形を作成します。
そして、AR空間の中に、無限に広がるフラクタルの世界を創造しましょう!
なお、ARプログラミング入門講座は、今回で最終回となります。
ここまで、Voxelammingの基本的な使い方から、様々なプログラミングの概念まで、幅広く学んできました。
この講座で得た知識を活かして、さらにVoxelammingの世界を探求し、あなただけのオリジナル作品作りに挑戦していきましょう!
中級講座は、準備ができ次第、改めて発表いたします。
お楽しみに!
読み始める前に
この記事では、私たちが開発した無料ARプログラミング学習アプリ「Voxelamming(ボクセラミング)」の使い方を、Pythonを使ったサンプルコードと共に詳しく解説していきます。
iPhone/iPad/Vision Proをお持ちの方は、App StoreからVoxelammingアプリをダウンロードして、ぜひ一緒にプログラミングに挑戦してみましょう!
この記事は、連載第1回目の内容を理解し、Pythonのインストール、voxelammingパッケージのインストール、そしてVS Code(または別のIDE)の設定が完了していることを前提としています。
前回の復習と今回の目標
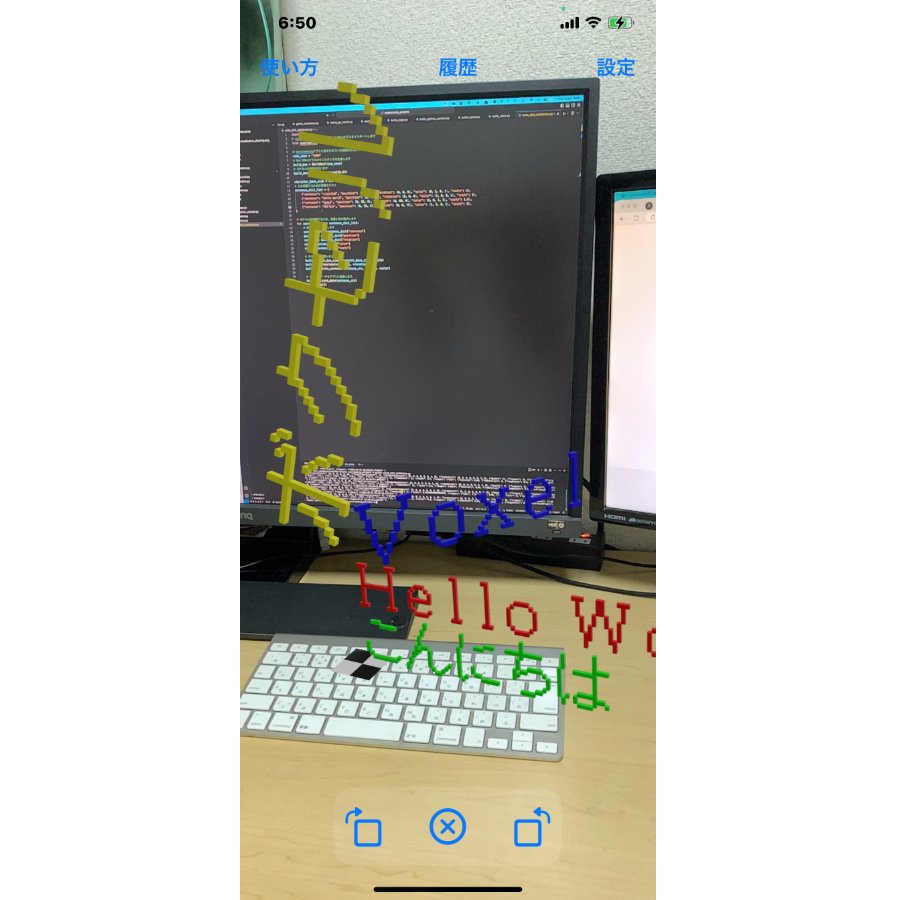
前回は、Voxelammingで文字を描画する方法を学びました。文字列を色や位置、角度を指定して、自由に配置できます。
write_sentence メソッドを使うことで、日本語や英語の文字列を、ボクセルで表現できました。
今回は、再帰関数を使って、Voxelammingでフラクタル図形を作成することを目標にします。
再帰関数は、自分自身を呼び出す関数のことです。
この再帰関数をうまく使うことで、フラクタル図形のように、複雑なパターンをシンプルなコードで表現することができます。
一見難しそうに思えるかもしれませんが、一つずつ丁寧に解説していくので、安心してください。
準備はいいですか?
それでは、Voxelammingでフラクタルの世界を探求する旅に出かけましょう!
今回使うPythonの知識
再帰関数:自分自身を呼び出す関数
再帰関数とは、その関数の中で自分自身を呼び出す関数のことです。
一見、不思議な概念に思えるかもしれませんが、再帰関数は、複雑な問題をシンプルに解決するための強力なツールであり、特にフラクタル図形の描画や、木構造のようなデータの処理に威力を発揮します。
再帰関数の仕組み
再帰関数は、問題をより小さな部分問題に分割し、それぞれの部分問題を解決することで、最終的に元の問題を解決します。
すべての再帰関数は、以下の2つの要素で構成されています。
ベースケース: 再帰呼び出しを終了するための条件。これを定義しないと、関数は無限に自分自身を呼び出し続け、プログラムが停止しなくなってしまいます。
再帰ステップ: 自分自身を呼び出して、より小さな部分問題を解決する処理。
再帰関数の適用例:フィボナッチ数列
再帰関数の威力を示す例として、フィボナッチ数列の計算を見てみましょう。
フィボナッチ数列は、最初の2つの項が1と1で、それ以降の項は前の2つの項の和となる数列です。
1, 1, 2, 3, 5, 8, 13, 21, ...フィボナッチ数列のn番目の項を計算する再帰関数は、以下のように定義できます。
def fibonacci(n):
"""
フィボナッチ数列のn番目の項を計算する関数
Args:
n (int): 求めたい項の番号
Returns:
int: フィボナッチ数列のn番目の項
"""
if n <= 1:
return 1 # ベースケース: 第0項と第1項は1
else:
return fibonacci(n - 1) + fibonacci(n - 2) # 再帰ステップ: n番目の項は (n-1)番目と(n-2)番目の項の和この関数を用いて、例えば fibonacci(6) を計算すると、以下のようになります。
fibonacci(6) = fibonacci(5) + fibonacci(4) = 13
fibonacci(5) = fibonacci(4) + fibonacci(3) = 8
fibonacci(4) = fibonacci(3) + fibonacci(2) = 5
fibonacci(3) = fibonacci(2) + fibonacci(1) = 3
fibonacci(2) = fibonacci(1) + fibonacci(0) = 2
fibonacci(1) = 1
fibonacci(0) = 1最終的に、fibonacci(1) と fibonacci(0) の値から、再帰的に計算が進んでいき、fibonacci(6) の値が 13 と求められます。
再帰関数の威力と注意点
一見シンプルに見えるフィボナッチ数列ですが、n が大きくなると、途方もない計算量になることがあります。
例えば、n = 30 の場合、フィボナッチ数列の30番目の項を計算するには、単純な for ループを使った方法では、なんと 30億回以上 も計算を行う必要があります! forループを使ったフィボナッチ数列を求める関数は次のような形になります。
def fibonacci_with_for_loop(n):
a, b = 1, 1 # 初期値
for _ in range(n):
a, b = b, a + b
return a大量の計算を行わなければならない理由は、forループでは、計算結果を保存(キャッシュ)することができないため、同じ計算を何度も繰り返してしまうからです。
一方、再帰関数を用いた fibonacci(n) では、わずか30回程度の計算 で結果を得ることができます。
これは、再帰関数が計算結果を効率的に再利用できる仕組みを持っているためです。
再帰関数の使いどころ
今回のテーマであるフラクタル図形の描画や、木構造のようなデータ構造を扱う場合、再帰関数は非常に強力なツールになります。
これらの処理では、問題を小さな部分問題に分割し、それらを再帰的に解決していくアプローチが適しています。
再帰関数は、このアプローチを自然に表現できるため、複雑な処理を簡潔なコードで記述することができます。
まとめ
再帰関数は、コードの簡潔さと計算効率の両方を兼ね備えた、強力なツールです。
単純な繰り返し処理では、for ループの方が効率的な場合もありますが、
問題を小さな部分問題に分割して解決できる場合は、再帰関数を使うことで、計算効率を大幅に向上させながら、コードをシンプルに記述することができます。
適切な場面で再帰関数を使うことで、複雑な問題をエレガントに解決できるようになるでしょう。
まとめ
今回は、再帰関数の仕組みについて解説し、フィボナッチ数列の計算を例に、その威力を示しました。
再帰関数は、最初は理解するのが難しいかもしれませんが、慣れると非常に強力なツールになります。
次の章では、これから作成するフラクタル図形について説明します。
フラクタル図形の知識
フラクタル図形とは?
フラクタル図形とは、一部分を拡大すると、全体と同じような形が現れるという、自己相似性 を持つ図形のことです。
自然界には、フラクタル図形とよく似た形をしたものがたくさん存在します。
例えば、木の枝分かれ、雪の結晶、海岸線、ロマネスコブロッコリーなどは、フラクタル図形の特徴である自己相似性を持っています。
フラクタル図形の例
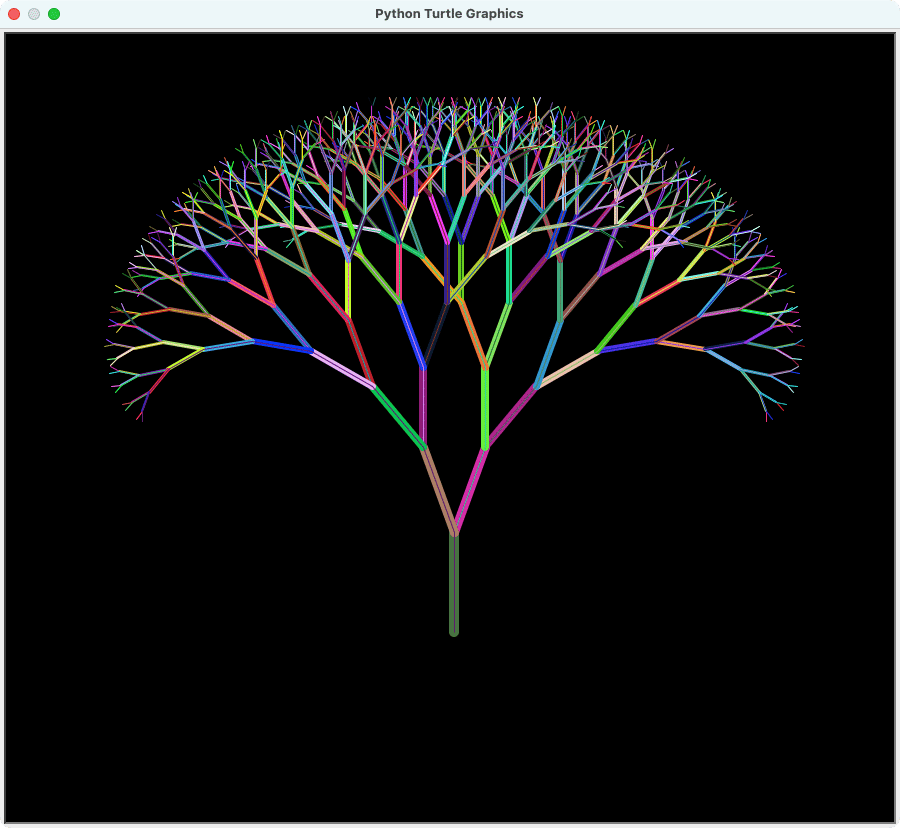
フラクタルツリー: 一本の線分から枝分かれを繰り返して生成される、木のような構造を持つ図形。各枝は、さらに小さな枝に分岐し、そのパターンが再帰的に繰り返されることで、複雑で自然な樹木の形状を模倣する。
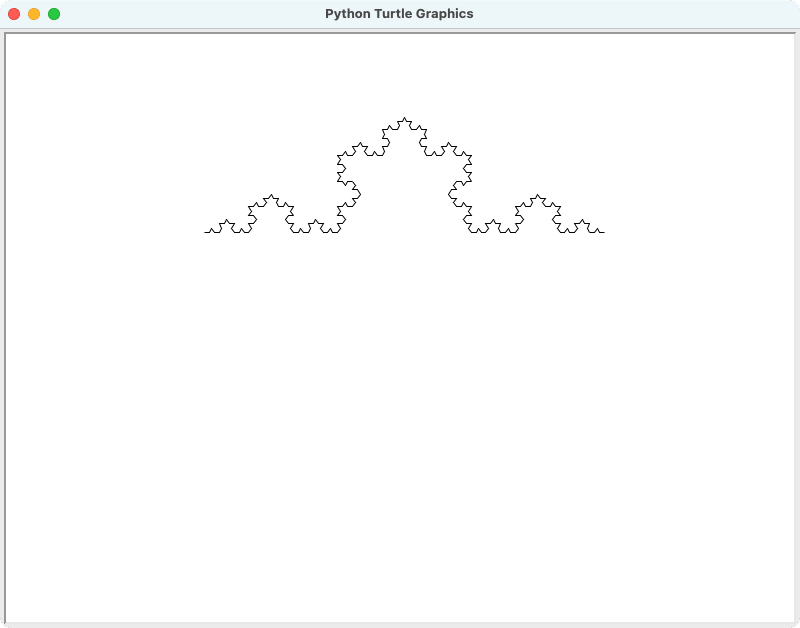
コッホ曲線: 直線を3等分し、中央部分を三角形に変形する操作を繰り返すことで生成される図形

シェルピンスキーの三角形: 正三角形から、中央の逆三角形を取り除く操作を繰り返すことで生成される図形
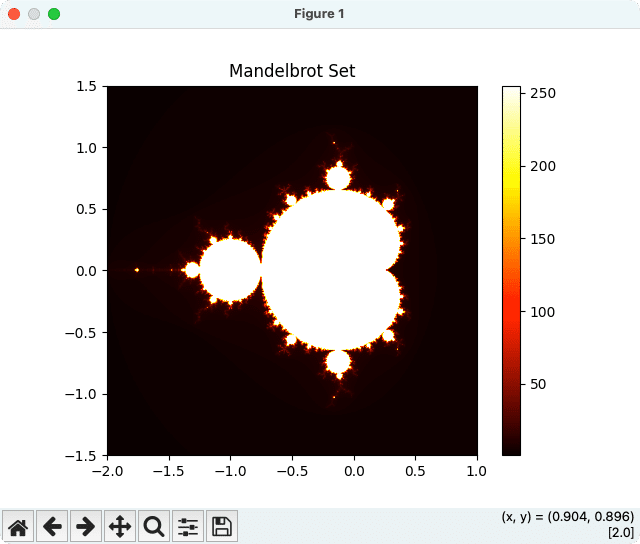
マンデルブロ集合: 複素平面上で定義される、非常に複雑な形状を持つフラクタル図形
フラクタル図形の美しさ
フラクタル図形は、その複雑さと自己相似性から、独特の美しさを持っています。
また、フラクタル図形は、数学的な規則性に基づいて生成されるため、その構造には神秘的な魅力を感じることができます。
フラクタル図形の応用
フラクタル図形は、その性質を利用して、様々な分野に応用されています。
コンピュータグラフィックス: 自然の風景や植物などをリアルに表現するために利用
アンテナ設計: 小型で高性能なアンテナの設計に利用
画像圧縮: フラクタル図形の自己相似性を利用して、画像データを効率的に圧縮
まとめ
今回は、フラクタル図形について解説しました。
フラクタル図形は、自己相似性という興味深い性質を持つ図形で、自然界にも多く存在します。
次の章では、再帰関数を使って、Voxelammingでフラクタル図形を作成していきます。
どんな美しいフラクタル図形がAR空間に現れるのか、お楽しみに!
サンプルコード解説
フラクタルツリーを描く
今回のサンプルコードでは、再帰関数を使って、Voxelammingでフラクタルツリーを作成します。
# voxelammingパッケージからVoxelammingクラスをインポートします
from voxelamming import Voxelamming
# 変数の設定
INITIAL_LENGTH = 10
REPEAT_COUNT = 5
ANGLE_TO_OPEN = 30
LENGTH_DECAY = 0.8
BRANCH_COLOR = [0.5, 0, 0]
LEAF_COLOR = [0, 0.5, 0]
# 色を計算する関数
def calculate_color(count):
r1, g1, b1 = BRANCH_COLOR
r2, g2, b2 = LEAF_COLOR
r = r2 - (r2 - r1) * count / REPEAT_COUNT
g = g2 - (g2 - g1) * count / REPEAT_COUNT
b = b2 - (b2 - b1) * count / REPEAT_COUNT
return r, g, b
# 三分木を描画する関数
def draw_three_branches(count, branch_length):
count -= 1
if count < 0:
return
# draw branches
length = branch_length * LENGTH_DECAY
color = calculate_color(count)
print("push_matrix")
vox.push_matrix()
# first branch
vox.transform(0, branch_length, 0, pitch=ANGLE_TO_OPEN, yaw=0, roll=0)
vox.draw_line(0, 0, 0, 0, length, 0, *color)
draw_three_branches(count, length)
# second branch
vox.transform(0, branch_length, 0, pitch=ANGLE_TO_OPEN, yaw=120, roll=0)
vox.draw_line(0, 0, 0, 0, length, 0, *color)
draw_three_branches(count, length)
# third branch
vox.transform(0, branch_length, 0, pitch=ANGLE_TO_OPEN, yaw=240, roll=0)
vox.draw_line(0, 0, 0, 0, length, 0, *color)
draw_three_branches(count, length)
print("pop_matrix")
vox.pop_matrix()
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
vox.set_box_size(0.5)
vox.set_build_interval(0.01)
vox.change_shape("sphere")
vox.set_command("float")
vox.draw_line(0, 0, 0, 0, INITIAL_LENGTH, 0, *BRANCH_COLOR)
draw_three_branches(REPEAT_COUNT, INITIAL_LENGTH)
vox.send_data("fractal_tree")上記のコードは、Voxelammingパッケージのバージョン0.3.0以降で有効です。それ以前のバージョンをインストール済みの方は「pip install --upgrade voxelamming」コマンドでアップデートを行なってください。
コード解説 パート1:準備と設定
最初の部分では、必要なパッケージをインポートし、フラクタルツリーの形状や色を定義する変数を設定しています。
from voxelamming import Voxelamming: Voxelammingを操作するための Voxelamming クラスをインポートしています。
INITIAL_LENGTH, REPEAT_COUNT, ANGLE_TO_OPEN, LENGTH_DECAY, BRANCH_COLOR, LEAF_COLOR: これらの変数は、フラクタルツリーの形状と色を定義しています。
コード解説 パート2:色の計算
calculate_color 関数は、枝の深さ (count) に応じて、枝の色を計算する関数です。
BRANCH_COLOR(茶色) から LEAF_COLOR(濃い緑) へと、徐々に色が変化していくように計算されています。
コード解説 パート3:三分木の描画
draw_three_branches 関数は、再帰関数を使って、三分木(3方向に枝分かれする木)を描画する関数です。
count: 再帰の深さを表す変数です。再帰呼び出しごとに1ずつ減っていき、0 になると再帰呼び出しを終了します。
branch_length: 枝の長さを表す変数です。再帰呼び出しごとに LENGTH_DECAY 倍に縮小されます。
再帰処理の流れ:
count が 0 より大きい場合は、以下の処理を繰り返します。
length を計算します。
color を計算します。
vox.push_matrix(): 現在の座標変換(位置や回転)をスタックに保存します。
3方向に枝を描画します。
vox.transform(...): 枝の始点に移動します。
vox.draw_line(...): 枝を描画します。
draw_three_branches(count, length): 再帰的に枝を描画します。
vox.pop_matrix(): スタックから座標変換を復元します。
count が 0 になった場合は、再帰呼び出しを終了します。
push_matrix() と pop_matrix() ~ 座標変換の積み木 ~
push_matrix() と pop_matrix() は、少し難しい概念ですが、Voxelammingで複雑な図形を描く際には非常に重要な役割を果たします。
これらのメソッドは、座標変換のスタック を操作します。
スタックとは、積み木のようにデータを積み重ねていくデータ構造です。
push_matrix() で座標変換をスタックに積み上げ、pop_matrix() でスタックから座標変換を取り出すことができます。
具体的なイメージ
あなたは、Voxelammingの世界で、木の枝を描こうとしています。
最初に、push_matrix() で現在の座標変換(木の幹の向き)を積み木に記録します。
次に、transform メソッドで枝の始点に移動し、draw_line メソッドで枝を描画します。
さらに、枝の先から新しい枝を描画するために、draw_three_branches 関数を再帰的に呼び出します。
再帰呼び出しが終わったら、pop_matrix() で積み木から座標変換を取り出し、元の木の幹の向きに戻ります。
2.~5.の処理を繰り返すことで、複雑な枝分かれ構造を持つ木を描画することができます。
push_matrix() と pop_matrix()のまとめ
push_matrix() と pop_matrix() を使うことで、座標変換を一時的に保存し、後で復元することができます。
これにより、複雑な図形を階層的に描画することが可能になります。
コード解説 パート4:フラクタルツリーの生成
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
vox.set_box_size(0.5)
vox.set_build_interval(0.01)
vox.change_shape("sphere")
vox.set_command("float")
vox.draw_line(0, 0, 0, 0, INITIAL_LENGTH, 0, *BRANCH_COLOR)
draw_three_branches(REPEAT_COUNT, INITIAL_LENGTH)
vox.send_data("fractal_tree")vox = Voxelamming(room_name): Voxelamming クラスのインスタンスを生成します。
vox.set_box_size(0.5): ボクセルのサイズを設定します。
vox.set_build_interval(0.01): ボクセルの設置間隔を設定します。
vox.change_shape("sphere"): ボクセルの形状を球に変更します。Voxelammingで選べる形状は「box(箱)」「sphere(球体)」「plane(平面)」の3つです。デフォルト値は box になります。
vox.set_command("float"): オブジェクトを空中に浮かせるコマンドを設定します。通常、ボクセルは(1,2,-3)のような整数の座標値にスナップ(吸い寄せられるように配置される)しますが、floatコマンドを送ると、小数点以下の値を持つ座標にもボクセルを配置できるようになります。このコマンドは精密なデザインを表現する時に使用します。
vox.draw_line(0, 0, 0, 0, INITIAL_LENGTH, 0, *BRANCH_COLOR): 最初の枝を描画します。
draw_three_branches(REPEAT_COUNT, INITIAL_LENGTH): 再帰関数を使ってフラクタルツリーを描画します。
vox.send_data("fractal_tree"): ボクセルデータを送信します。
この章では、再帰関数を使ってフラクタルツリーを作成するコードを解説しました。
次の章では、このコードを実行し、Voxelammingアプリで美しいフラクタルツリーをAR表示してみましょう!
サンプルコードを実行する
それでは、いよいよサンプルコードを実行して、AR空間にフラクタルツリーを出現させてみましょう!
1. ルーム名を確認
まず、Voxelammingアプリを起動し、画面中央に表示されているルーム名を確認してください。
2. ルーム名をコードに反映
サンプルコードの room_name 変数の値を、アプリに表示されているルーム名に書き換えます。書き換え後、保存するのを忘れないようにしてください。
room_name = "XXXX" # XXXXをアプリのルーム名に書き換える3. コードを実行
VS Codeでターミナルを開き、次のコマンドを実行します。
ターミナルからコマンドを実行する
python fractal_tree.pyプログラムが正常に実行されると、Voxelammingアプリ上に、フラクタルツリーが現れます。親枝が3本の子枝に分かれる細部構造を持ち、全体が部分の相似形であるフラクタルが立体で表現されています。
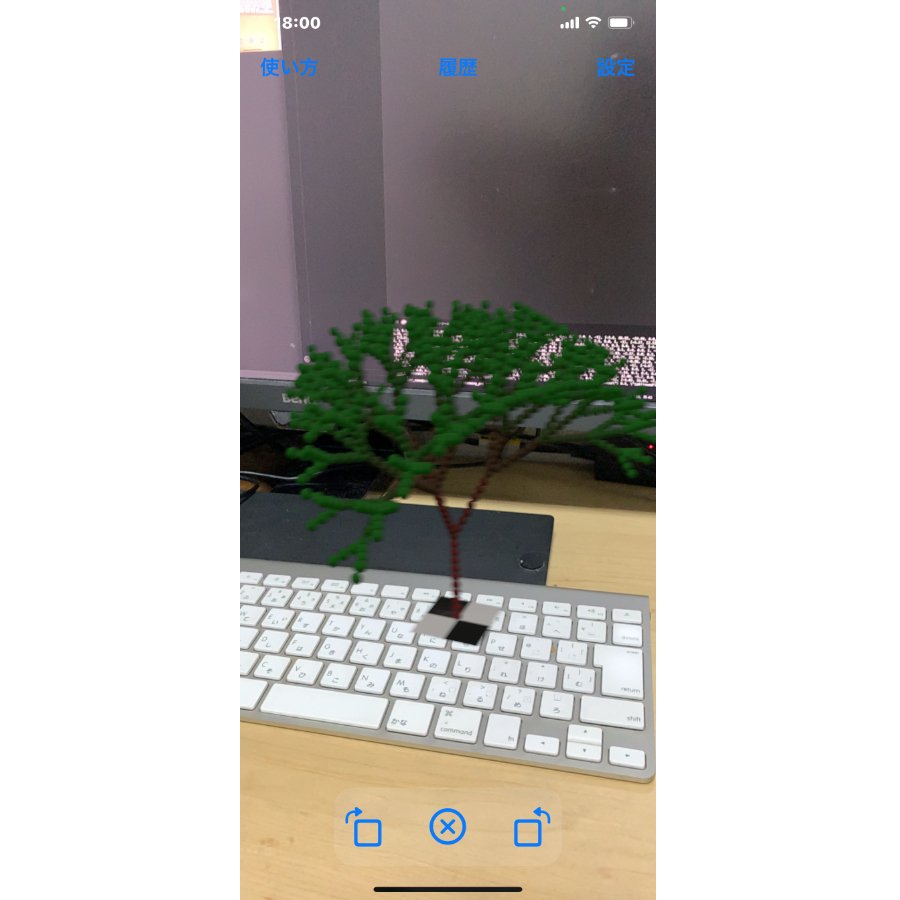
実行できないときは
もし、うまく文字が描画されない場合は、以下の点を確認してみてください。
Voxelammingアプリとパソコンが同じWi-Fiネットワークに接続されているか
サンプルコードの room_name 変数の値が、アプリに表示されているルーム名と一致しているか
回線が混み合っている場合は、時間をおいてから再度、コマンドを実行してください。
次の章では、応用として、今回作成した文字表示プログラムを改造して、オリジナル作品作りに挑戦してみましょう!
応用:オリジナル作品作りに挑戦!
問題1: フラクタルな雪の結晶を作ろう!
再帰関数を使って、雪の結晶のような美しいフラクタル図形を作成してみましょう。
挑戦する前に
自分で考えてコードを書いてみると、プログラミングの理解がより深まります。時間がない方は、回答例を参考にしてください。
回答例
VS Codeで「snowflake.py」という名前のファイルを作成し、以下のコードを記述してください。
from voxelamming import Voxelamming
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
vox.set_box_size(0.2)
vox.set_build_interval(0.01)
vox.set_command('liteRender')
# 雪の結晶の枝の長さ
branch_length = 30
# 枝分かれ角度
angle = 60
def snowflake_branch(length, level):
if level == 0:
return
vox.push_matrix()
vox.draw_line(0, 0, 0, 0, length, 0, 1, 1, 1)
length *= 0.8
vox.transform(0, length, 0, 0, 0, -angle)
snowflake_branch(length, level - 1)
vox.transform(0, length, 0, 0, 0, 0)
snowflake_branch(length, level - 1)
vox.transform(0, length, 0, 0, 0, angle)
snowflake_branch(length, level - 1)
vox.pop_matrix()
# 雪の結晶を描画
for i in range(6):
vox.push_matrix()
vox.transform(0, 0, 0, 0, 0, 60 * i)
snowflake_branch(branch_length, 4)
vox.pop_matrix()
vox.transform(0, branch_length * 2, 0, 0, 0, 0)
vox.send_data("snowflake")解説
このコードでは、snowflake_branch という再帰関数を定義し、6回呼び出すことで六角形の雪の結晶を描画しています。
snowflake_branch 関数は、枝の長さ (length) と再帰レベル (level) を引数に取ります。
再帰レベルが 0 の場合は、処理を終了します。
再帰レベルが 0 より大きい場合は、以下の処理を繰り返します。
白い線を描画します。
枝の長さを縮小します。
3方向に枝分かれを描画します。
vox.transform(...): 枝の始点に移動します。
snowflake_branch(length, level - 1): 再帰的に枝を描画します。
このプログラムを実行すると、立体的な案内表示を作成できます。指定した方向に矢印が向いているので、平面の案内表示よりも直感的に移動することができます。
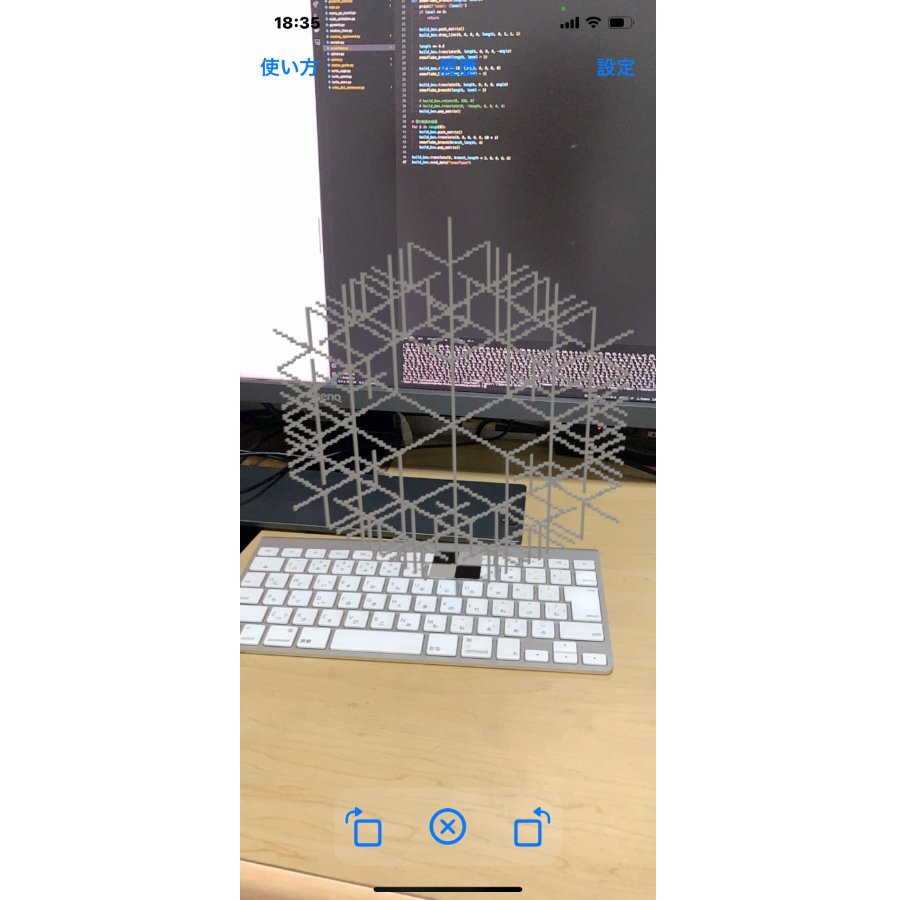
ポイント
vox.set_command('liteRender'):レンダリングを簡素化することで、デバイスの負荷を低減しています。このコマンドは設置するボクセルの数が多い時に有効な対策になります。
vox.transform(...), vox.rotate(...): これらのメソッドを組み合わせて、雪の結晶の枝分かれを表現しています。
push_matrix() と pop_matrix(): これらのメソッドを使って、座標変換のスタックを操作することで、各枝の描画を独立させています。
問題2: シェルピンスキーの三角形を作ろう!
今度は、シェルピンスキーの三角形と呼ばれるフラクタル図形をVoxelammingで表現してみましょう。
平面ではなく、立体的なシェルピンスキーの三角形に挑戦してみましょう!
回答例
VS Codeで「sierpinski_triangle.py」という名前のファイルを作成し、以下のコードを記述してください。
from voxelamming import Voxelamming
# Voxelammingアプリに表示されている部屋名を指定してください
room_name = "1000"
# Voxelammingクラスのインスタンスを生成します
vox = Voxelamming(room_name)
vox.set_box_size(0.1)
vox.set_build_interval(0.01)
vox.set_command('liteRender')
# 三角形の辺の長さ
side_length = 200
def sierpinski_triangle(x, y, z, length, level):
"""
シェルピンスキーの三角形を描画する関数
Args:
x (int): 三角形の頂点のx座標
y (int): 三角形の頂点のy座標
z (int): 三角形の頂点のz座標
length (int): 三角形の辺の長さ
level (int): 再帰レベル
"""
if level == 0:
# 三角形の3つの頂点の座標を計算
p1 = [x, y, z]
p2 = [x + length, y, z]
p3 = [x + length / 2, y + length * 0.866, z] # 0.866は√3/2
# 三角形の3辺を描画
vox.draw_line(*p1, *p2, 1, 0, 0)
vox.draw_line(*p2, *p3, 1, 0, 0)
vox.draw_line(*p3, *p1, 1, 0, 0)
return
# 再帰的にシェルピンスキーの三角形を描画
half_length = length / 2
sierpinski_triangle(x, y, z, half_length, level - 1) # 左下の三角形
sierpinski_triangle(x + half_length, y, z, half_length, level - 1) # 右下の三角形
sierpinski_triangle(x + half_length / 2, y + half_length * 0.866, z, half_length, level - 1) # 上の三角形
# シェルピンスキーの三角形を描画
sierpinski_triangle(0, 0, 0, side_length, 6)
vox.send_data("sierpinski_triangle")
解説
sierpinski_triangle 関数: シェルピンスキーの三角形を描画する再帰関数です。
再帰レベルが0の場合は、通常の三角形を draw_line メソッドで描画します。
再帰レベルが0より大きい場合は、三角形を3つの小さな三角形に分割し、それぞれに対して再帰的に sierpinski_triangle 関数を呼び出します。
p1, p2, p3: 三角形の3つの頂点の座標を計算しています。p3 のy座標は、正三角形の高さを計算して求めています。
このプログラムを実行すると、立体的なシェルピンスキーの三角形が描かれます。従来のシェルピンスキーの三角形は平面図形ですが、このコードではz座標を導入することで、3次元空間上に立体的なシェルピンスキーの三角形を描画しています。
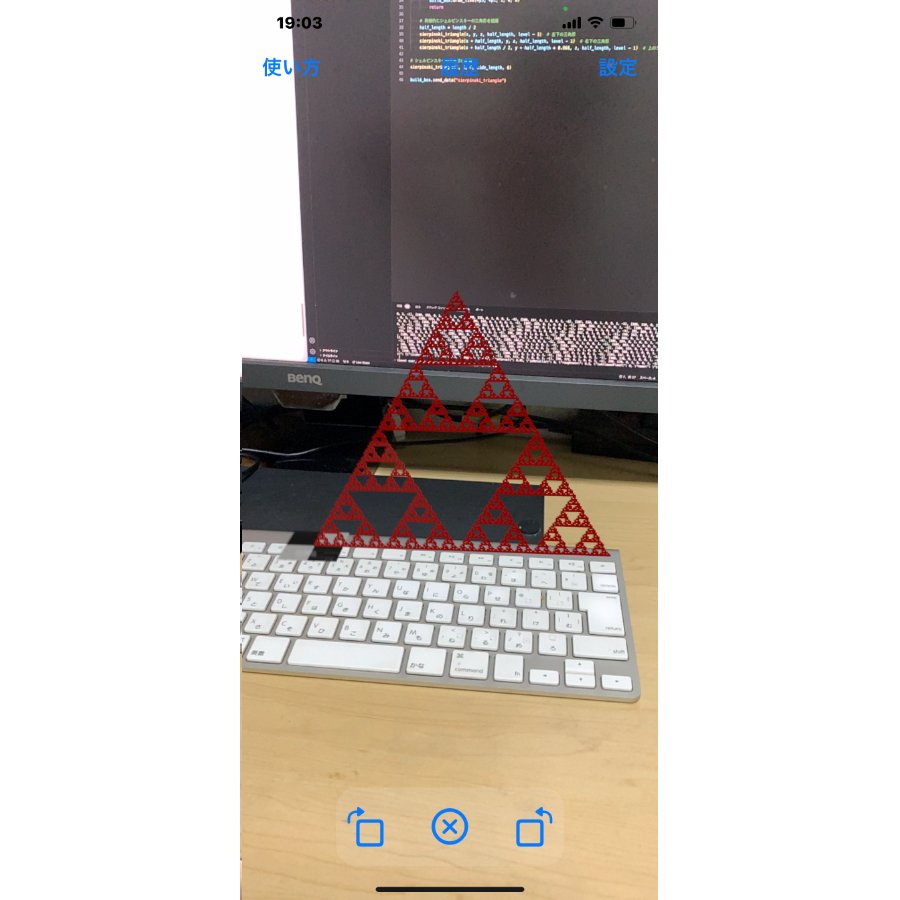
挑戦してみよう!
再帰レベルを変更して、シェルピンスキーの三角形の分割レベルを調整してみましょう。
三角形の辺の色や太さを変えてみましょう。
複数のシェルピンスキーの三角形を組み合わせて、より複雑な形を作ってみましょう。
まとめ
ARプログラミング入門講座、ついに最終回を迎えました!
この講座を通して、あなたはVoxelammingの世界を探求し、様々なプログラミングの概念を学び、AR空間上に創造力を爆発させてきました。
ボクセルを配置して、シンプルな形から複雑な形まで、様々なオブジェクトを作り出す方法を学びました。
色や大きさを変えたり、回転させたりすることで、表現の幅を広げました。
条件分岐を使って、プログラムをより賢く制御する方法を習得しました。
ランダムな要素を取り入れて、予測できない、個性的な作品を生み出しました。
アニメーションで、作品に命を吹き込みました。
文字列を描画して、AR空間にメッセージを刻みました。
そして、再帰関数という魔法のようなテクニックを使って、フラクタル図形という、複雑で美しい世界を創造しました。
ここまで、本当に素晴らしい挑戦の連続でしたね!
時には難しい概念に頭を悩ませ、時にはエラーに苦戦したかもしれません。
それでも、諦めずに、一歩ずつ着実にVoxelammingの世界を歩んできたあなたを、心から称賛します! 👏
この講座は終わりを迎えますが、あなたのプログラミングの旅は、まだ始まったばかりです。
Voxelammingで培ったプログラミングの知識と経験は、今後、様々な場面で活かせる貴重な財産となるでしょう。
これからも、好奇心と創造力を胸に、プログラミングという大海原を、勇敢に航海していってください!
Voxelammingチーム一同、あなたのさらなる活躍を応援しています! 🚀✨
AR プログラミング入門シリーズ
ARプログラミング入門シリーズの一覧です。全8回で完結します。
次回、中級編は構想中です。ご期待ください!
第1回 Voxelammingについて
第2回 ボクセルアートの色と形を変えてみよう!
第3回 球体を作る
第4回 ランダムな線でアートを描こう!
第5回 アニメーションで命を吹き込もう!
第6回 タートルグラフィックスで図形を描こう!
第7回 文字でAR空間にメッセージを描こう!
第8回 再帰関数でフラクタルに挑戦!
サンプルコードを公開
GitHubレポジトリでサンプルコードを公開しています。記事を読むときに参照してください。
