ワンピースの数学的解釈
※数学に関して厳密なことは一切書いていません。特に図形用語は不適切な使用があります。
ワンピースといえば言わずと知れた国民的漫画だが、その作者、尾田栄一郎先生が質問コーナー、通称SBS内で興味深い話をされていた
女性のプロポーションは「丸3つ、バツ1つ」
こう考えて描いてください。
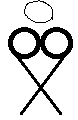
非常にシンプルだ。
この画像に数学を感じたので図形として見てみる。
図形として考えると乳円(ちちえん)の接線をへそから引くと胴体になる。
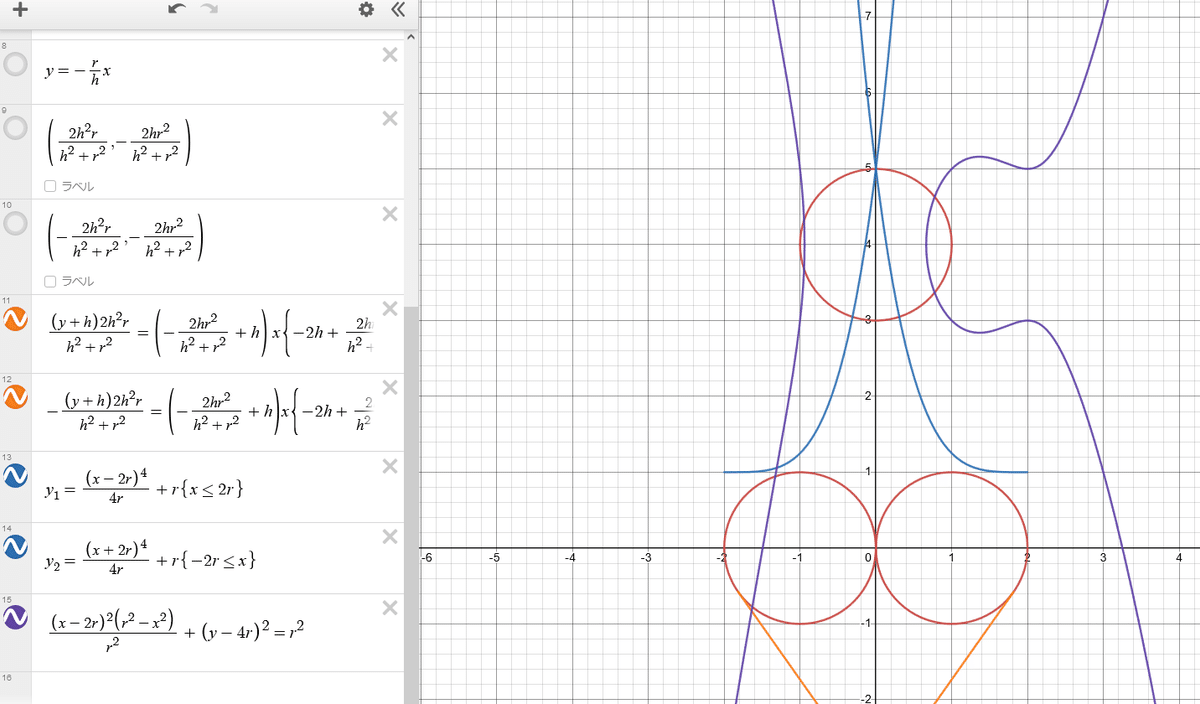
まず関数アートを描くのに使われるらしいDesmosというツールで乳円を描く。
後の計算が楽そうなので胸の谷間の真ん中を原点にする。
式は$${(x-r)^2+y^2=r^2 , (x+r)^2+y^2=r^2}$$。rが乳半径になる。

そして顔のサイズと首の長さは元絵の乳のサイズとの縮尺を大まかにとって乳:首:顔を$${2:1:2}$$とした。

丸3つができたので、次は胴体部分のバツ1つに行こうと思う。
うまいやり方が思いつかなかったのでへその位置を決めてそこから円との接線を引く方法で描く。
書いてるこっちもよくわかっていないので数学得意じゃない人にもわかる説明で書きたい。
へそを$${(0,-h)}$$(hは谷間からへそまでの長さ)の点にする。
ここから数学苦手が奮闘する様子なので冗長な数式が出てきます。
まずどうやって接点を求めるんだっけ。
今原点と円の中心とへその3点がわかってるからそこから求めよう。
とりあえずへそと乳首をつないだ。

へそから乳に引ける接線の接点は二個あってそのうちの一つが原点だから原点に線対称な点がわかればそことへそをつないでバツが描けるんじゃないかな〜〜

$$
y=\frac{r}{h}x-h
$$
に関して原点に対称な点が接点になる。ちょっと対称とか難しいから垂直な線を引く。原点を通る直線なので$${y=ax}$$
$$
\frac{r}{h}a=-1\\
a =-\frac{h}{r}\\
y=-\frac{h}{r}x
$$

なんかいい感じに代入して計算すると
$$
\begin{array}{} r^2 &=& (x-r)^2+(-\frac{r}{h}x)^2 \\\ &=& x^2-2xr+r^2+\frac{r^2x^2}{h^2} \end{array} \\\
\begin{array}{} 0 &=& x^2-2xr+\frac{r^2x^2}{h^2}\\\ &=& xh^2+xr^2-2h^2\end{array}\\\
x=\frac{2h^2r}{h^2+r^2}
\begin{array}{} y &=& -\frac{r}{h}\times\frac{2h^2r}{h^2+r^2}\\\ &=& -\frac{2hr^2}{h^2+r^2}\end{array}\\\
(\frac{2h^2r}{h^2+r^2},-\frac{2hr^2}{h^2+r^2})
$$
関数グラフに入力する分には複雑な分数でも構わなかったけど計算するとなると非常にだるい!!!!!!!!!!!!!!!!!!!
2点を通る直線はぱぱっと代入するだけして
$${y=\frac{-\frac{2hr^2}{h^2+r^2}+h}{\frac{2h^2r}{h^2+r^2}}x-h}$$
$${\frac{(y+h)2h^2r}{h^2+r^2}=(-\frac{2hr^2}{h^2+r^2}+h)x,-\frac{(y+h)2h^2r}{h^2+r^2}=(-\frac{2hr^2}{h^2+r^2}+h)x,{-2h+\frac{2hr^2}{h^2+r^2}>=y>=-\frac{2hr^2}{h^2+r^2}}}$$

首や肩を描きたいけど正確な曲線を描こうとすると大学数学が出てきて難しすぎます。

首と顔の接点を求めるのがめちゃくちゃ難しいです。
やっぱ難しいんで高校数学までに習う簡単な二次関数で表せる放物線を首にします。

ここで挫折しました。
全部感覚でウエストと腕を描いてこの記事を終わらせようと思います。

この記事のアイデアはこの記事のURLを張ってくれれば自由に使ってください。ハッシュタグは #尾田関数チャレンジ で各々の尾田関数をアレンジして完成させてSNSでシェアしよう!
もっと数学出来る人がフーリエ変換とか正弦波とか使って完成させてくれたらうれしいです。
ただ、数式を記事上で表す際のTeX記法はめちゃくちゃめんどくさいです。
終わり
この記事きっかけで関数アートに限らず新しいことに挑戦する人が出てきてくれたら幸いです。
あとこの記事は性的なコンテンツではなく、教育的な目的で書きました。
次回は、『数学的にイガラムを解説』でお会いしましょう。さようなら。
