
Titanicデータセットで生死分類モデルを構築~線形SVM~
こんにちは、コグラフ株式会社データアナリティクス事業部の平松です。
今回はTitanicのデータセットを使って「生存・死亡」の分類モデルを作成します。
コードではデータの前処理からモデル作成まで詳しく解説をしているので、是非参考にしてみて下さい。
可視化、データ分析、仮説立て、前処理からモデル構築まで一連のフローを学びたい方は必見です!
はじめに
機械学習モデルを作成する際に大事なことは
①最終的に何をしたいのか目的を明確にすること、②EDA(探索的データ分析)、③モデル作成前のデータ処理です。
なぜなら、
目的を明確にしないと、どんなライブラリ、どんなモデルを作成するかわからないからです。どんなに精度が高くても、目的から逸れたモデルを構築しては役に立ちません。
データ分析を行い、どんな説明変数をセレクトするかで精度は大きく変わります。
データの前処理を行わないと、モデルが動かないことや、かろうじて動いたとしても精度が低くなる場合があるからです。
モデル作成において前処理が80%の部分を担っていると私は思っています。
モデル構築の目的
Titanicのtrainデータセットを使用して、生存、死亡の分類モデルを構築します。ここではサポートベクタマシーンの分類モデルであるLinearSVCをモデル構築に使います。
なぜなら①目的が生死ラベルの予測であり、②すでにラベルが存在しており、③データポイントが10000未満であるからです。
今回の、一連のフローは下記の通りです。
ライブラリのインポート
概要把握
型の処理
可視化
データ分析
仮説立て
データの前処理
モデル構築
評価
再構築
ざっくり言い換えると、
①具材と調理器具をそろえ、②具材をさばき、③どんな具材を調理すべきかを選別し、④下ごしらえ、④鍋にぶち込む、⑤味を調整するといった具合です。
対応は以下の通りです。
具材と調理器具をそろえるー1.ライブラリのインポート、2.概要把握
具材をさばくー3.型の処理、4.可視化、5.データ分析
どんな具材を調理すべきかを選別ー6.仮説立て
下ごしらえー7.データの前処理
鍋にぶち込むー8.モデル構築
味を調整するー9.評価、10.再構築
※今回は8.モデルの評価、9.再構築は除きます。
データセットは以下になります。
ライブラリインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
from scipy import stats
from sklearn.preprocessing import StandardScaler, RobustScaler
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVCここでは、最初にライブラリを用意しました。一般的には分析を進めていく過程でライブラリをインポートしていきます。
なぜなら、どんな検定やモデル構築をするのか分析して見ないとわからないことが多いからです。
前処理にpandas、numpy、可視化にmatplotlib、seaborn、検定にscipy、正規化にsklearn.preprocessing、データ分割にsklearn.model_selection、モデル構築にsklearn.svmを使います。
概要把握
df = pd.read_csv("----------\\titanic_train.tsv", sep='\t')
print(df.describe(), df)
出力から読み取とれることを挙げる前に、カラムの説明をしておきます。
id:乗客識別ユニークID
survived:生存フラグ。0=死亡、1=生存(カテゴリ変数)
pclass:チケットクラス。1が最も高いクラス、3が最も低いクラス(カテゴリ変数)
sex:性別。male=男性、female=女性(カテゴリ変数)
age:年齢(連続変数)
sibsp:タイタニックに同乗している兄弟/配偶者の数(カテゴリ変数)
parch:タイタニックに同乗している親/子供の数(カテゴリ変数)
fare:料金(連続変数)
embarked:出発港。S = Southampton、C = Cherbourg、Q = Queenstown(カテゴリ変数)
このデータからわかることは、ageのcountがほかのカラムより少ないこと、データポイントが445あることです。
また、fareのmean(平均)は33.9、std(標準偏差)は52.0に対して、maxが512.3と大きな外れ値があることが分かります。
それに関してはsibsp、parchにも当てはまります。
計算方法は「mean + (std × 2) >= max」です。これは信頼区間95%を表しています。
dfのみの出力(出力結果下部)からわかることはsexとembarkedがstr型であることです。
従って、データを分析しやすくするため、sexとembarkedをint型に変更します。
df['sex'] = df['sex'].map({'male': 0, 'female': 1})
df['embarked'] = df['embarked'].map({'S': 0, 'C': 1, 'Q': 2})
print(df)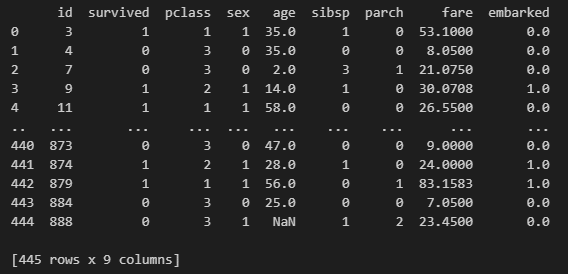
ダミー変数への変更はpandasの関数であるget_dummies()やone-hot-encodingライブラリでも可能です。是非調べてみて下さい。
male(男性)→0、female(女性)→1
S(Southampton)→0、C(Cherbourg)→1、Q(Queenstown)→2
のようにstrをintに変換しました。
次に可視化を行います。
可視化・分析
まず最初にデータの分布を見ます。
理由はざっとデータの雰囲気を把握するため、気になるポイントを見つけるため、のちにどんな処理を加えるか確認するためなどが代表的です。
df.hist(figsize=(12, 10))
plt.show()
分布から読み取ったことは、
全体的にカテゴリ変数が多い
idを抜いて、fareとageしか連続変数がない
fareは分布にかなりの偏りがあるが、対照的にageはベル型に近い分布をしている
次に、目的変数になるsurvivedごとのcountをカラム別に観察していきます。
fig, axes = plt.subplots(2, 3 ,figsize=(14, 14))
sns.countplot(data=df, x="sex", hue="survived", ax=axes[0, 0])
sns.countplot(data=df, x="sibsp", hue="survived", ax=axes[0, 1])
sns.countplot(data=df, x="pclass", hue="survived", ax=axes[0, 2])
sns.countplot(data=df, x="embarked", hue="survived", ax=axes[1, 0])
sns.countplot(data=df, x="parch", hue="survived", ax=axes[1, 1])
sns.displot(data=df, x="fare",col='survived')
上記2つの絵からわかることは、
女性の方が男性より全体の人数が少ないが、生存者数は男性より多い
sibspは0人が圧倒的に多い=一人で来た人が多い
pclassが1の人が少なく、唯一、生存者数の方が死亡者数より多いクラス
死亡者全体のうち半数以上がpclassが3の人である
Southampton港から来た人が多い
Cherbourg港から来た人は生存者の方が死亡者より多い
parchが0人の人が大半を占めていて、比例して死亡者数の大半もparchが0人の人
fareが安い人が多く、それに伴い死亡者も群を抜いて多い。
次に、連続変数などの特定の分析をします。
fig, axes = plt.subplots(2, 2 ,figsize=(14, 12))
sns.boxplot(data=df, x='survived', y='fare', ax=axes[0, 0])
sns.boxplot(data=df, x='survived', y='age', ax=axes[0, 1])
sns.regplot(data=df, x="age", y="fare", ax=axes[1, 0])
sns.regplot(data=df, x="pclass", y="fare", ax=axes[1, 1]) 
上記の絵からわかることは、
生存している人の方が、高い料金を払っている傾向にある
生存している人の方が、年齢が若い傾向にある
年齢と料金にはほんの少しの正の相関関係にある
もちろんのことだが乗船クラスの数値が低くなるほど料金が高い傾向にある
次に、乗船クラスと料金が生死に影響を与えていることがそれぞれわかったのでクラスと料金に生死ラベルの凡例を加えて可視化してみます。
sns.swarmplot(data=df, x="pclass", y="fare", hue='survived')
plt.show()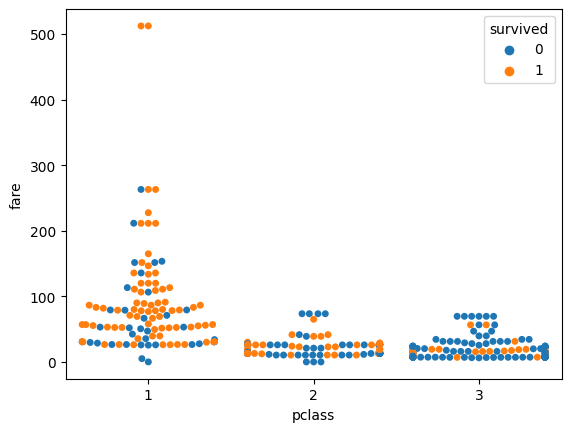
結果は一目瞭然で、料金が低いpclassが3の人の生存数は少ないです。
次に目的変数を中心にそれぞれの特徴量の相関関係を見てみます。
df.corr()
数値で出してみたが少し見づらく、見落としてしまいそうなので、heatmapを使って可視化してみます。
sns.heatmap(df.corr(), annot=True)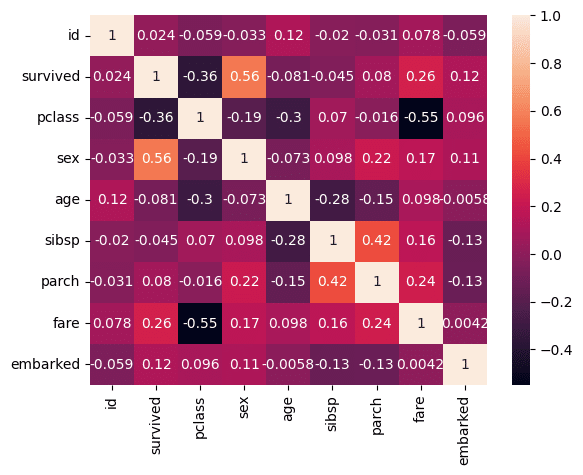
まず、上から2行目のsurvivedとの関係性を見てみます。
survivedとの関係性は、sex、pclass、fareの順番の3つが比較的高いと言えます。
説明変数同士だと、fareとpclass、fareとparch、parchとsibsp、pclassとage、ageとsibspが際立って見えます。
仮説(推測されること)
これはどの説明変数を入れるのかを考えることに繋がります。
女性の方が生存しやすい
pclassがの数字が低いほど生存しやすい
料金が高いほど生存しやすい
料金が高いほど、pclassの数字が低くなる傾向がある
料金が高いほどparchの人数も多い傾向にある
料金が高いほどsibspの人数も多い傾向にある
女性であるほどpclassの数字が低い傾向にある
女性であるほどsibspの人数が少ない傾向にある
次は、分布が正規分布に則っているか確認を行います。
data = df['age']
data2 = df['fare']
plt.figure(figsize=(14, 8))
plt.subplot(121)
stats.probplot(data, dist='norm', plot=plt)
plt.subplot(122)
stats.probplot(data2, dist='norm', plot=plt)
plt.show()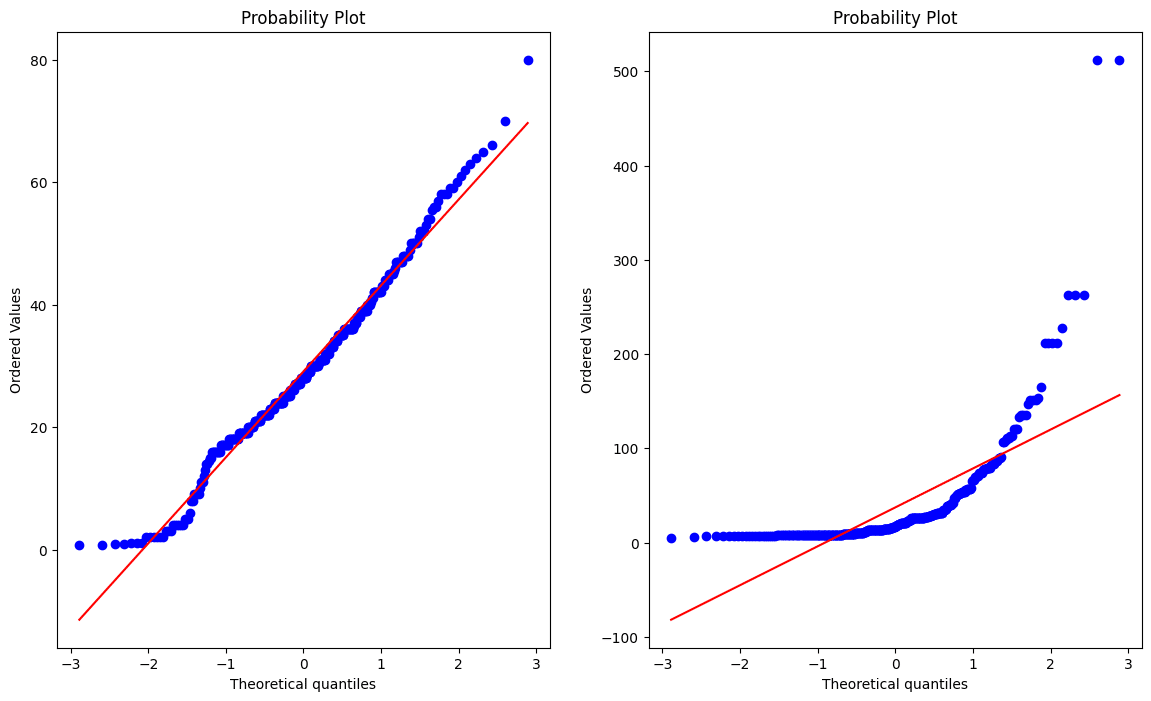
Q-Qプロットで確認を行います。
Q-Qプロットとは、観測値が正規分布に従う場合の期待値をY軸にとり、観測値そのものをX軸にとった確率プロットです。
プロットが一直線上に並べば、観測値は正規分布に従っていると考えられます。
上記の絵は左がageと右がfareのQ-Qプロットです。
ageは直線に近い形をしているが、fareは直線上にプロットが殆ど乗っていません。
従って、ageは正規分布の可能性はあり得るが、fareは正規分布とは言えないという仮説が立てられます。
print(stats.shapiro(df["fare"]))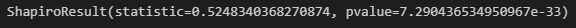
結果、p値(pvalue)<0.05なので棄却域に入ります。
従って、正規性があるという帰無仮説を棄却し、fareの母集団には正規性はない、という結果になります。
もう一度分布を見てみましょう。
df[['age', 'fare']].hist(bins=50, figsize=(8, 6))
plt.show()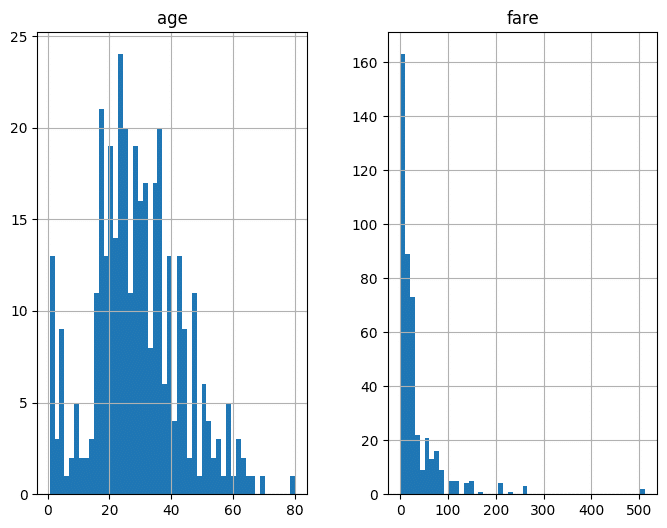
確かに、ageの分布はベル型に見えますが、fareは左に偏った分布となっています。
次に、スケーリングを行います。
これは④下ごしらえに当たる部分です。
基本的に、外れ値の除去問題やスケーリング(下ごしらえ)には多くのやり方があり、現在も研究が進められている分野です。
今回の場合、ageは標準化、fareはロバストスケーリングで正規化を行います。
from sklearn.preprocessing import RobustScaler
age_scaler = StandardScaler()
fare_scaler = RobustScaler()
df['age'] = age_scaler.fit_transform(df['age'].values.reshape(-1, 1))
df['fare'] = age_scaler.fit_transform(df['fare'].values.reshape(-1, 1))
df[['age', 'fare']].hist()
plt.show()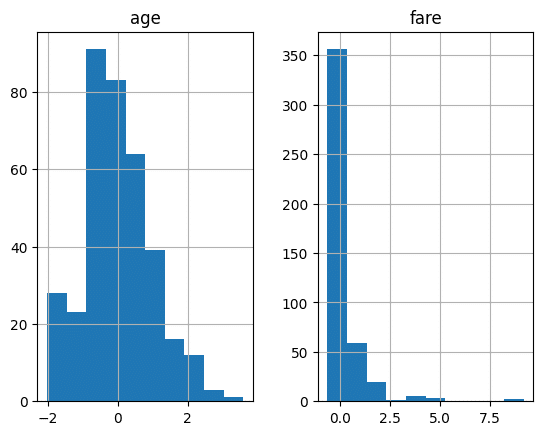
StandardScalerとは、データを平均0、分散1となるように標準化する手法です。
RobustScalerとは、中央値を目安にスケーリングを行う手法です。
他にも様々なスケーリング方法があります。
例えばや、MinMaxScalerという、データを0~1の範囲に収めるように正規化する手法などがあります。
この手法は外れ値の影響を受けやすいので一様分布に従っているデータをスケーリングすることに適しています。
また、場合によっては外れ値を除去することなどもあり得ます。
この辺りは是非ご自身で調べてみて下さい。
次は、欠損値を処理していきます。
まず、特徴量ごとの欠損値数を把握します。
df.isnull().sum()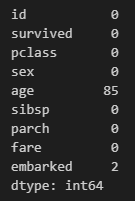
このように、ageには85個、embarkedには2個の欠損値が存在することが分かります。
この欠損値を除去していきます。
df = df.dropna()
print(df.describe())
df.isnull().sum()
このように、欠損値はすべてなくなり、
データポイントがもとの445個-(85個+2個)=358個になりました。
それは出力結果1行目のcountで確認できます。
次に、データセットを分割し、モデル構築に入っていきます。
使用するモデルはサポートベクターマシーン(SVM)の分類器です。
SVMでは、それぞれのクラスで、その直線に最も近いデータ点(Support Vector)を考え、そのデータ点と直線との距離(マージン)が、できるだけ大きくなるように直線を決定します。
ラベルが既についているデータセット(教師あり学習)で、データポイントが10万未満、分類を目的に置いている場合に有効です。
学習手法では、完璧な分類を目指すために学習データに対して過度にフィットさせようとした結果、overfittingが起きてしまいます。
overfittingにより、新しいデータの予測精度が悪化してしまいます。
一方、SVMは「マージン最大化を行うこと」が目的のため、overfittingのリスクが少なく、誤検知を出しにくい点がメリットです。
「マージン」とは、クラスの分類基準となる境界と各データとの距離のことです。
従って、「マージン最大化」は、つまり2つのサポートベクトル(境界から最も近いデータ)から最も遠い位置に境界線を設定することを意味します。
モデル構築
y = df['survived']
X = df[['sex', 'fare', 'pclass', 'age']]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
SVC = LinearSVC().fit(X_train, y_train)
score = SVC.score(X_test, y_test)
print(score)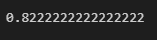
説明変数はsex、fare、pclass、ageです。
途中の説明変数を省く手順と評価、再構築は省略します。
結果、分類の正答率(精度)は82.2%でした。
また、説明変数は同じ条件でスケーリングを行わずにモデル構築した場合、の精度は72.2%でした。
説明変数にすべての特徴量を使い、スケーリングを行わずにモデル構築した場合、の精度は65.5%でした。
EDAによる特徴量の選別、スケーリングは十分に精度を高めるに寄与し、この精度は、相対的によいと判断できるでしょう。
データ分析に興味のある方募集中!
コグラフ株式会社データアナリティクス事業部ではPythonやSQLの研修を行った後、実務に着手します。
研修内容の充実はもちろん、経験者に相談できる環境が備わっています。
このようにコグラフの研修には、実務を想定し着実にスキルアップを目指す環境があります。
興味がある方は、下記リンクよりお問い合わせください。
Twitterもやってます!
コグラフデータ事業部ではTwitterでも情報を発信しています。
データ分析に興味がある、データアナリストになりたい人など、ぜひフォローお願いします!
📢Wantedly新掲載!
— アラリコ@コグラフ株式会社 | データ事業部 (@CographData) July 14, 2023
「データに興味がある」
「データに携わる仕事がしたい」
そこのあなた!
私たちと一緒にデータ分析しませんか?
IT業界未経験の方も大歓迎です☺️#エンジニア転職 #データ分析 #駆け出しエンジニアと繋がりたいhttps://t.co/S9o7VSjGRt
この記事が気に入ったらサポートをしてみませんか?

