大妻女子中学の理科(物理)研究

概要・主旨

理科の勉強効率を上げるために入試問題を研究する。
傾向とレベルを把握して逆算的に子供に指導するためだ。

まず物理からやってみて化学地学生物もやっていく。
ということで23年と22年から合計3回分を見てみる。

問題レベルの確認

合格ラインの確認。
80%を求められるのと50%で良いのとは全然違う。

合格最低点と合格者平均点。
公式サイトから抜粋。

4教科合計の合格最低点から各教科の合格者最低点を類推。
以下の通り理科は50%くらいが合格最低点ぽい。

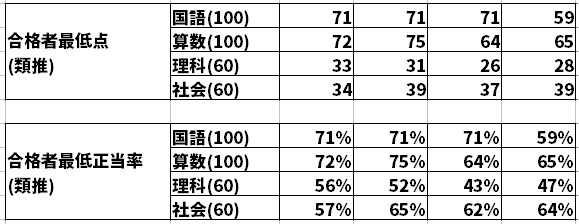
50%ってことは各大問毎に前半の小問を解けばよい感じ。
では問題を見ていく。

2023年2月1日の問題

小問1：圧力

重さを底面積で割って比べる。
圧力の計算って中学受験の範囲なのか。

適当に重い順に並べても正解になってしまうのは設問として微妙。
逆転するようにして欲しい。計算し損やん。

小問2：ばね

一番重いおもりを長い方のばねにつるしたときの長さを読み取るだけ。

小問3：浮力

浮力の計算で沈んでる体積を出す。
水面に出てる部分の高さを比較。

小問1~3は基本に見える。
ここまでが合格者想定正答問題っぽい。

小問4：ばねと浮力の複合

浮力分を引いてばねの長さを出す。
グラフからはみ出しているのでばねののびの理解も必要。

これが応用的な位置づけっぽい。
合格最低点としては不要だけど加点ポイント。

小問5：ばねと浮力の複合

水深と浮力が関係ないことがわかってるかどうかの理解を問う問題。
小問4で出した答えを使えば計算は不要。

2023年2月2日の問題

小問1：振動の周期性(グラフの読み取り)

物理やってると自明だけど小学生にはどうなのか。
小問1は基本のはずだから多分習ってるんだろう。

理解出来てなくてもグラフから9.5秒でどうなるか類推可能。
もしかしたらグラフの読み取りが本命かも。

小問2：事象の理解

文章読んで事象を理解できるかという問い。
小問2にしては難易度高めに見える。
2月1日の小問1,2に比べて難易度高いような。

小問3：事象の理解

実験1と2の内容を理解してどうなるか類推する。
なんだかんだこういうのは難問、子供には難しい。

小問4：理科知識の現実世界への類推

入試でよく見る日常に波及させるタイプの問題。
時事ネタっぽくもしてる。

小問5：波が伝わる速さ

波長2倍だから波の早さ2倍。
落とす速さ2倍だから落とす間隔は1/2。

2022年2月1日の問題

小問1はばねののび、グラフの読み取り

ばねの全体長ではなくのびを見る、という基本。

小問2は並列のばね

AとBが同じ長さになるとこをグラフから読み取る。
ばねが並列なら重さを分担できるから重さ読み取った値の2倍。

小問3はばねとてこの複合

グラフから足して120gになる長さを探す。
40g:80g=1:2に荷重したいから2:1の点。

合否の分岐となる小問3。
23の2月1日より難しいけど、23の2月2日より簡単なイメージ。

小問4は直列のばね

直列につないだ際の挙動を知ってれば割と基本。
小問3より難易度低そう。
てこの流れで小問3を先に出したけど、小問4が分岐点問題かも。

小問5はばねを分割

ばねを分割した際の挙動は習うのか不明。
それとも原理から類推するのか。

40gつるすとばねBは25cmから35cmに伸びる。
直列の考えからばねBの10㎠部分にも15cm部分にも40gかかってる。

ばねは均等に伸びるはず(ここが既知なのか類推なのか)ので、
15cm部分が21cmに、10cm部分が14cmに伸びたはず。

10cm部分を21cmまで伸ばすには11cm伸ばす必要がある。
15cm部分に40gで6cm伸びだった場合と比較すると以下。

必要な伸びが11cm/6cm倍。同じ重さでの伸びが4cm/6cm倍なので、
40g×11cm/6cm÷4cm/6cm=110g

別解：10cmを11cm伸ばして21cmにするということは。
25cmなら11cm×25/10=27.5伸ばして52.5cmにする必要がある。
グラフから52.5cmは110g。

いずれにせよ結構難しそう。
これは加点問題っぽい。

総括

基本問題と分岐点問題と加点問題に分けれそう。
まずは基本問題と子供のレベルの間を埋める練習がよさげ。