
大妻中学校の算数完全攻略 #直前対策有り
2年3回分の過去問から問題の傾向と対策を解説。
まず合格ライン。
公式HPでの結果は以下の通り。
ここから推定する。
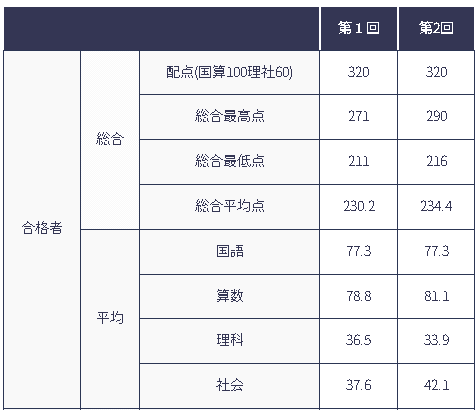
例えば第1回の最低点は211。
これを平均点の比で分けると算数は72
#211×78.8÷(77.3+78.8+36.5+37.6)=72.2・・・
合格平均230.2を平均点の比で分けると算数は79
第2も同様に計算すると最低点は75、合格平均は81
つまり算数苦手でも7割~7割5分は必要で得意なら8割以上欲しい。
ではどの問題で7,8割取っていくか個別に見ていく。
計算問題
最初は以下のような2問の計算問題。
この傾向は過去数年変わってないので今年もそうだろう。

難易度は高くない。
とはいえ計算ミスは誰にでも起こる。
今からいくら計算練習してもミスの確率はそう変わらない。
対策としては、途中式を書く練習をすること。

途中式を素早く正確に(部分点がもらえるように)書けるようにする。
それだけでも計算ミスリスクをかなり抑えられる。
計算問題の途中式の練習なんて1日5分合計1,2時間もやれば十分。
それくらいの時間は作れるだろう。
基本問題
計算問題の後に4,5問の基本問題が続く。
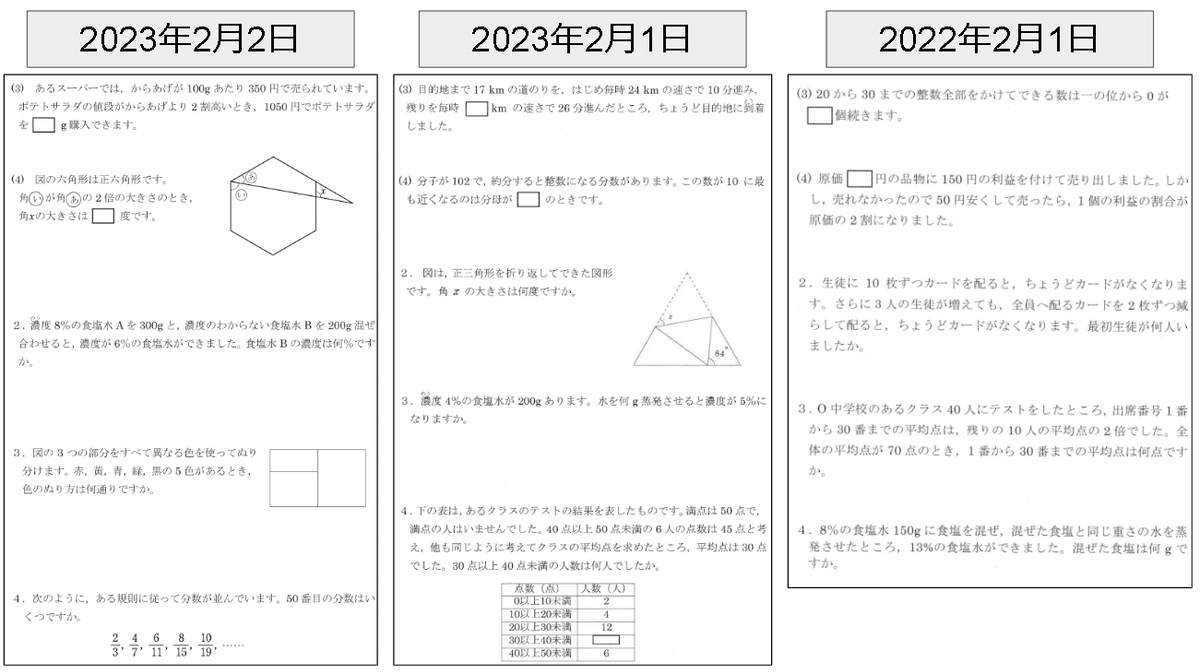
一度は見たことのあるような頻出の基本問題が出る。
ジャンルもわりと固定されている。
損益、濃度、角度、平均、整数あたりが頻出だ。
これらの基本問題は確実に迷わずに解けるようにしておきたい。
とはいえ大妻レベルを目指す子が今更この辺りの基本を抑えれてないわけがないので特に対策は不要だろう。
敢えてやるなら時間を決めて途中式を書く練習をすると試験対策になる。
基本問題の小問4,5問にかけれる時間は10分程度だろう。
同じレベルの基本問題を5問用意して10分で途中式まで書かせる。
間違えたり迷ったり時間がかかるジャンルを重点的に繰り返す。
もしやるならそんな感じの対策で良いと思う。
応用問題1:文章問題
後述する図形問題の前に出る中難易度くらいの問題。
図形の後に高難易度の問題として出る場合もある。

中難易度の方は7,8割取るには落とせないレベル。
ほぼほぼ必ず旅人算が出ている。
後は数列、比が頻出。
旅人算はほぼ100%出るのでしっかり対策しておくと良い。
数列もここで出るか基本で出るかはしてるので同様に対策必須。
数列は分数関連の整数問題っぽい数列が出やすい印象。
高難易度の方が結構レベルが高い。
以下のニュートン算くらいの高難易度は最悪捨てても良いかも。
頻出じゃないから対策しづらいし。

応用問題2:図形
終盤に図形が複数問出題される。
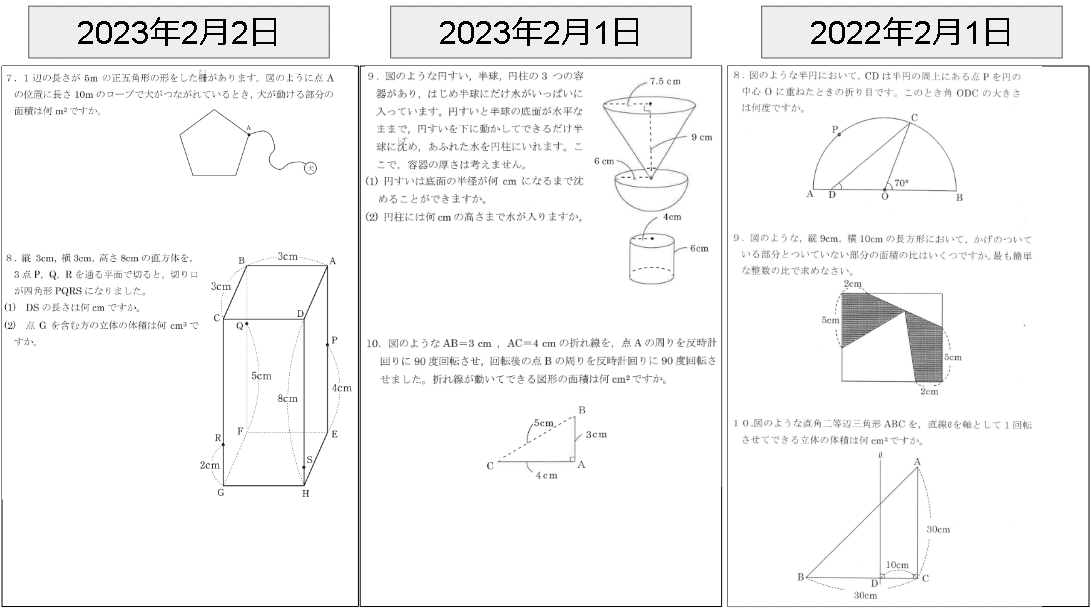
平面の面積と立体の体積という組合せが多い。
そこまで高難易度ではない。
平面も立体も回転や移動系が多いように感じるので、それ系の問題は特に練習しておくと良いだろう。
回転や移動系が多いということは円周率絡みの計算ミスが怖い。
対策として円周率の2~9倍は覚えても良いと思う。
30分~1時間もあれば覚えれるだろうし結構コスパ良い。
パップスギュルダンと切頭四角柱の公式も覚えておきたい。
これらは覚えるだけでなく使いこなすために練習が必要。
対策を書いてきたが解くという意味では特効薬的な対策はなく、これまで培ってきた図形の実力が試されるだろう。
応用の難易度が高い1割の問題は全員落とすとして、残り9割の内、図形で3割は配点ありそう。
6割の基本と中級を落とさず、図形3割で何割取れるか。
