第3回チップシの腕っぷしヤジリン大会大会問題解説
どうもchipです。
この記事は、2022年3月5日22:00-23:30に行われた第3回チップシの腕っぷしヤジリン大会の大会問題「Don't go straight」の想定解き筋の解説になります。
かなり難しめの手筋を使うので記事での解説を行います。(「MASTER」の解説よりはちょっと雑になるかも)
問題

めちゃでかい すごいでかいな ばかでかい(初期盤面川柳)
解説
まずは初期埋めから。

終わりです(?????)
何も手掛かりがないように見えますがちゃんと解けますのでご安心を
まずはこの問題の(サイズ的に)デカい配置の謎を解いていきましょう。

問題の右上の方にあるこの配置、実は一意に定まります。
例えば下図の赤のマスが黒マスだと仮定すると、線が下に伸びていきます。
しかしその場合、青のマスも黒マスになるので横の1→が破綻してしまいます。

よって赤のマスは白マスであることがわかります。そしてこの白マス埋めの考えはほかのマスにも同様のことが言えるため、このようになります。

よってこの配置は最終的にこのように決まります。

これを大会問題にも同じように適用させてこうなります。

次は盤面右下、3→と3つの2↓に注目します。

3→において、左側に2つ黒マスを置くとします。
するとその下にある3x5の領域に黒マスを6つ置かなければならなくなり、どうやっても配置するのが不可能なので破綻することがわかります。
よって右側に黒マスが2つ置かれることが分かります。

これにより、丸印の2→の黒マスが一つ確定します。
さらにこの黒マスにより、いずれにせよ論法から赤丸部分は必ず線が伸びます。

次に先ほど伸ばした線の下、赤枠の部分を考えます。

この部分は先ほど黒マスが埋まっていることから2↓1↓2↓に置き換えられます。
すると黒マスの置き方は2通りになります(3列充填)

さらにこのとき、黒マスと線がいずれにせよ論法から少し伸ばすことができます。

これにより上の画像の右上の1↓が決めることができます。

青のマスは横の2↓により必ず白マスに、赤のマスは黒マスを入れようとすると横の2↓との兼ね合いで線が詰まったり小ループが発生したりして破綻することが分かります。なので最終的に緑のマスが黒マスが入ります。
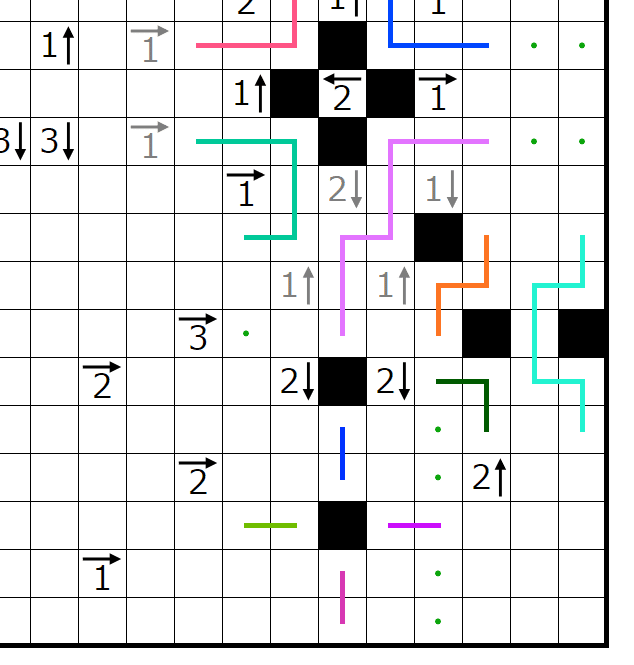
さあここで先ほど軽く紹介した3列充填なんですが、もう一つある性質があります。

上図のように、3x3n-1(nは自然数)の領域に対して入る黒マスがn,n-1,nのとき、横に抜ける線はn本になります。

これを踏まえると、上図の赤枠の左から2本線が入ります。
よって地味に偶奇!!!!!!!!!!!!!!!!!


次は右端の方を見てみます。

→1において、赤のマスに黒マスを置くと線が分岐して破綻します。
青のマスに黒マスを置くと偶奇が破綻します。
すると、上下にある2↑,2↓がどちらの黒マスの置き方でも消化されるので白マスがある程度確定します。

↓↓↓

これにより赤丸の2→において、青のマスは黒マスを置くと線が分岐するため白マスに、赤のマスは黒マスで確定します。
さらに、赤のマスが黒マスになるので3列充填の黒マスがすべて決まります。

↓🌸↓🌸↓
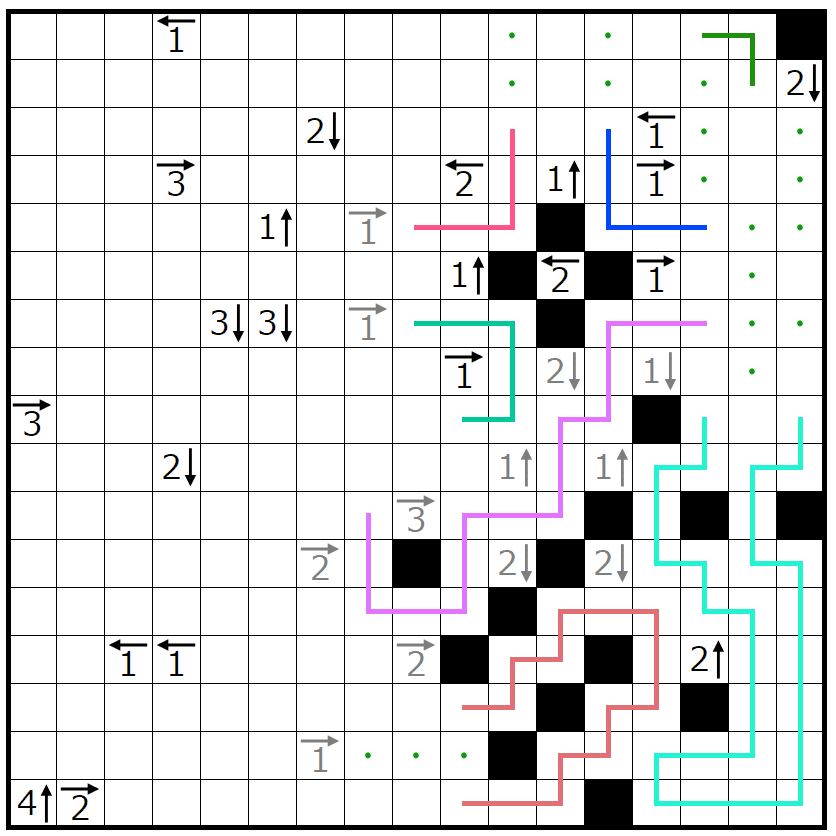
ここまで埋まると右端の1→がすべて決まります。


次は盤面の左側の3↓3↓を解いていきます。
ここではT字充填というテクニックを使います。

2列充填の派生(?)で上下の端以外の領域がヒント等込みで十字に区切られるとき、図のようにそれぞれの色で塗られた領域には多くても黒マスが1マスまでしか入りません。(説明が難しい)

大会問題だとこのように区切られます。このとき、領域は全部で6つで赤色の領域は1マスしかないので自動的に黒マスが確定します。

オレンジの領域も黒マスが確定します。

左の赤丸から線が一本伸びるので地味に偶奇!!!!!!!!!!より×印には線が入ってきません。

緑の領域の黒マスも確定します。

下図の盤面下において、ピンクの四角の場所に線が通ると小ループができて破綻するので×印になります。
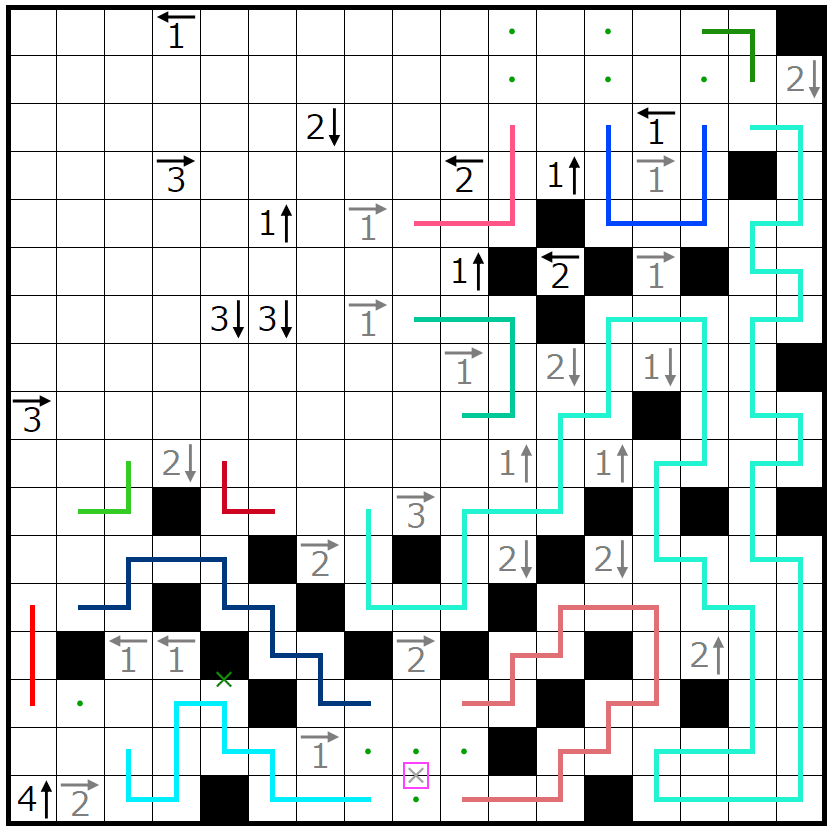
そして大域小ループ禁!!!!!!!!!!
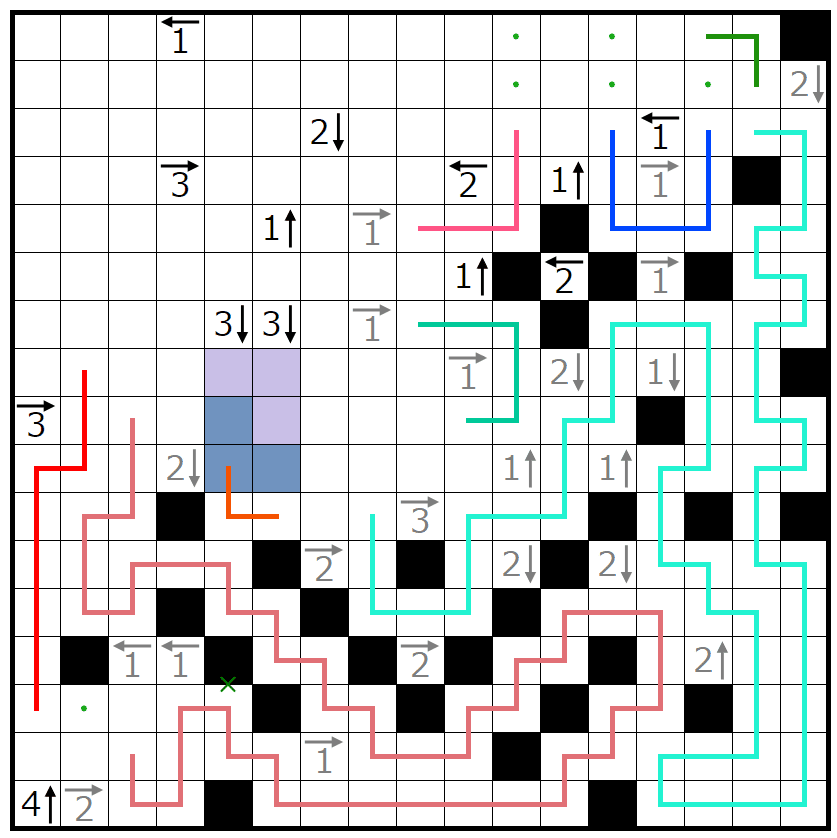
そして残りの領域のうち、紺色の領域は上に黒マスを置くと紫の領域に黒マスを置けなくなるので右に黒マスを置くことが分かります。

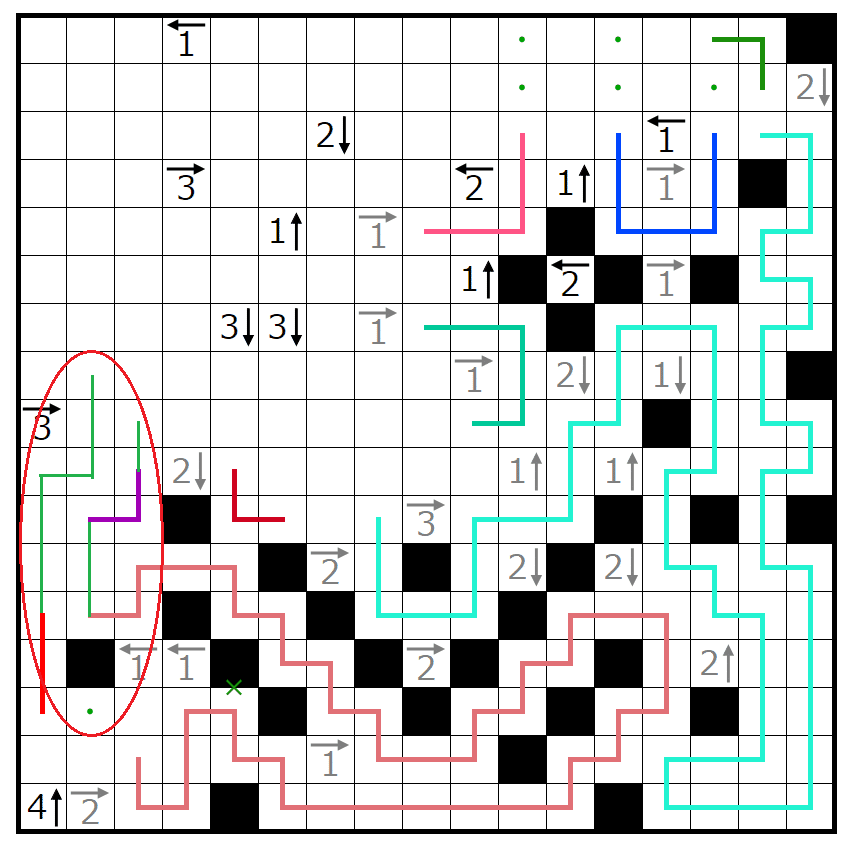
次に見るのはこの部分。
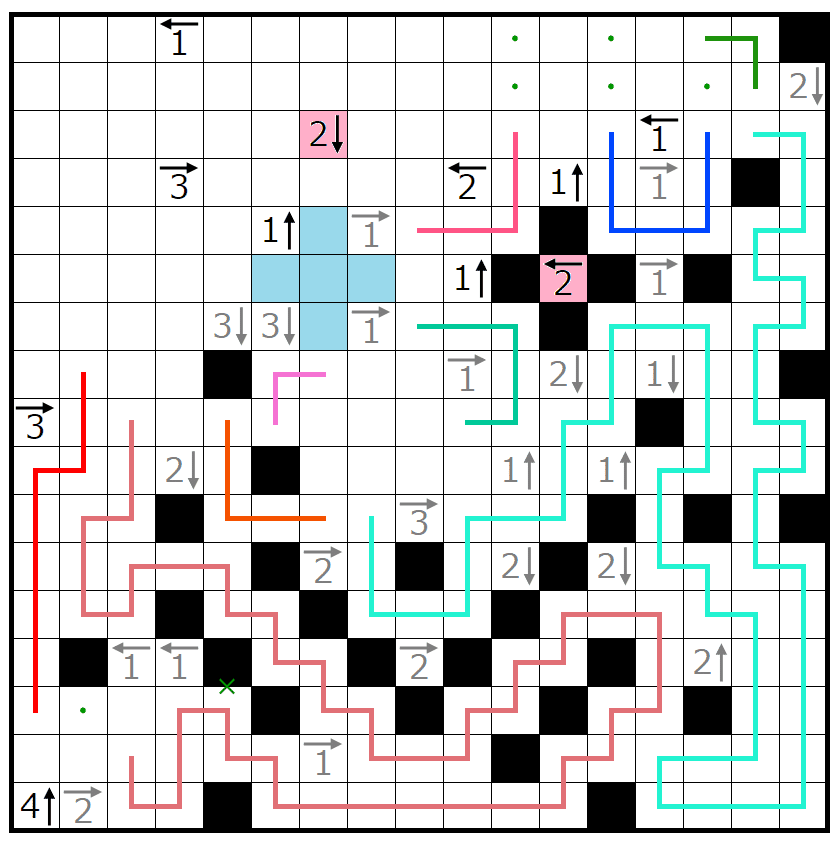
赤のヒントはそれぞれすでに黒マスが1つ使われています。
そこで青色の領域を一直線に貫こうとすると黒マスの数が破綻してしまいます。

よって青色の領域で線が曲がる必要がありますが、そうするとどう曲がっても青色の領域で黒マスをすべて消費することになります。
よって、赤色のマスはすべて白マスになります。
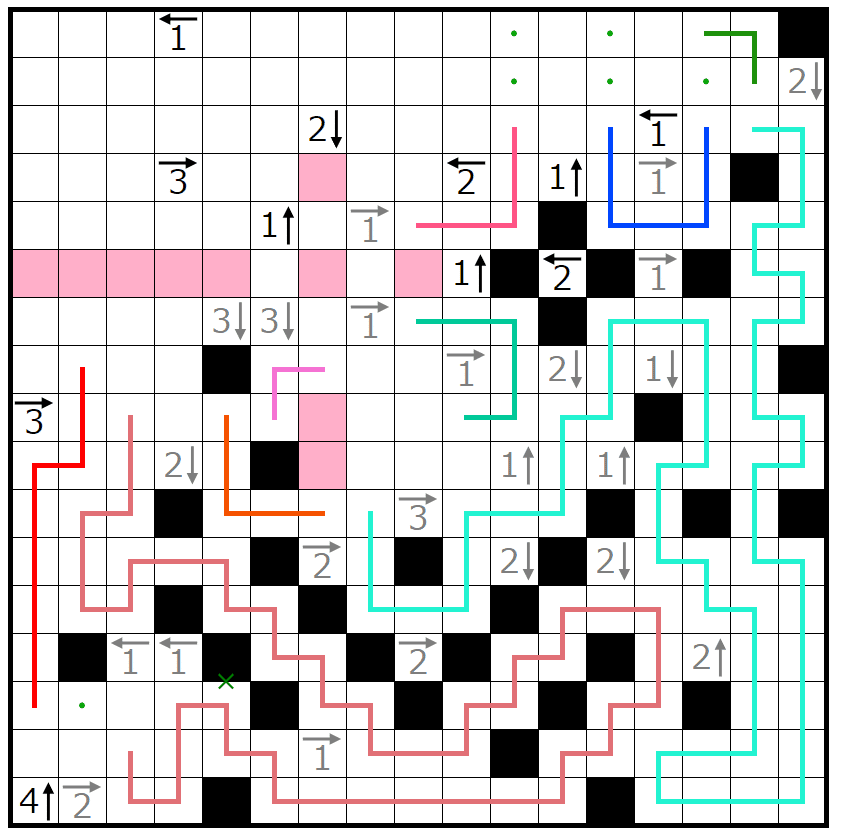
これで左端の3→が埋まります


地味に偶奇!!!!!!!!!

どんどん埋めていって・・・

辺の定理と大域小ループ禁!!!!!!!!!!!!!!

ラストスパート🌸🌸して・・・

1↑に対して黒マスが下の方だと偶奇が破綻するので・・・

残りを🌸て完成です!!!!!!!!!!!!!!!お疲れさまでした!!!!!!!!!!!!!!!!!!!!
終わりに
終盤かなり駆け足でしたが以上で解説終了です!
最初の配置や3列充填、T字充填など入れたい配置を全部入れられたのでかなり納得のいく問題になりました。
一応優勝タイムは5分ぐらいだろうな~と予想してるんですがどうなるんでしょうか(大会前日に大急ぎで執筆しました)(4時間近くかかった)
参加者多いといいな~~~~~~(願望)
普段は不定期でヤジリンを作りつつSOUND VOLTEXメインで音ゲーの鍵盤しばいてたり、Dancing☆Onigiriで譜面を作ったり、最近はあんまりできてないですが作曲をしたりしています。興味あればぜひ見てみてください~
Twitter(https://twitter.com/chipstar64)
chip creation(http://chipstar64.sakura.ne.jp/danoni.html)
