
コロナがもしきてなかったら...."Python初心者"が時系列分析で訪日外国人数を予測してみた。
・はじめに
貴重なお時間ありがとうございます。
Aidemy Premiumにて「データ分析コース」を3ヶ月受講いたしました。
Aidemy Premiumを受講したのは、データ分析、機械学習、Pythonをしっかりと学びそれを活かして仕事をしていきたいと思ったことが、きっかけでした。
AI、機械学習、ビックデータ、データ活用とたくさんのデータに関するワードを耳にするようになりました。
ただ、実際に調べてみると意味のわからない横文字(例. ディープラーニング)、聞いたことのない日本語(例. 深層学習)、思考停止に見るのをやめてしまう数式(例. 𝐶𝑜𝑣(𝑦𝑡,𝑦𝑡−𝑗)=𝛾𝑗)が多くなかなか理解できないケースが多くあるかと思います。
記事を書く1番の目的は知識を定着させることですが、
少しでも皆様と知識や経験をシェアできるようにレベルをあげていきます。
実際にPythonで実装した内容で記載しております。
わかりにく表現もあるかと思いますが、よろしくお願いいたします。
・実行環境
Jupyter Notebook
Python 3.7.3
目的
今回の目的はコロナウイルスが発生していなかったら、どれくらいの外国人がどれくらい日本に来ていたのかを予測することです。良いモデルを作り、訪日外国人数を予測し、”もしもコロナがなかったら。。。”の比較をしてきます。
早速いきましょう!
・そもそも時系列分析とは?
過去のデータを分析し未来を予測すること。
会社の売り上げや商品の売り上げ予測、さらには来店者数の予測など、ビジネスにおいて非常に重要な分析技術となります。
時系列分析の第一歩は、時系列データを 視覚化することが大切です。
グラフにし確認することでさまざまなことがわかります。
例えば下記のパターンがあります。
・原系列
なにもされていない時系列データそのものは 原系列と呼ばれます。時系列分析の目的はこの 原系列 の性質を探って行くことです。時系列分析において 原系列 そのものを扱うことはあまりありません。実際には時系列データを加工し新しい系列にして、それを分析して モデル を構築していきます。
・時系列データのパターン
時系列データには トレンド、 周期変動、 不規則変動の3つのパターンがあります。
1. トレンド
データの長期的な傾向を意味します。時間の経過とともにデータの値が上昇していたり下降していたりする時系列データは「トレンドがある」といい、値が上昇している場合には 正のトレンド 下降している場合には 負のトレンド があると言います。
2. 周期変動
周期変動があるデータは時間の経過に伴ってデータの値が上昇と下降を繰り返します。特に1年間での周期変動を 季節変動 といいます。
3. 不規則変動
時間の経過と関係なくデータの値が変動することをいいます。
用語集
分析に行く前にここで時系列分析を行うにあたり抑えておかないといけないこと、いくつか考え方を紹介します。
1. 自己相関、偏自己相関
2. 定常性
3. 対数系列
4. 移動平均
5. 階差系列
6. 季節調整の利用
7. ホワイトノイズ
1. 自己相関、偏自己相関
・自己相関
簡単に言うと 過去の値が現在のデータにどれくらい影響しているかを現した値。時系列上にある異なる点同士の相関のことを自己相関と言います。回帰分析が他データとの関係を考慮するのに対し、時系列分析は自分自身のデータの前後の関係を考慮する点です。自己相関を用いることで、データの前後の関係を表現します。
例えば、月次データの場合、一つずらして自己相関を確認すれば、一月前の値が今月にどれくらい影響しているかが分かります。
自己相関はコレログラムというグラフで表すことができます。
・偏自己相関
具体的に説明します。7日間差の自己相関係数を求めたとします。しかし、ある日のデータが前日のデータと相関があった場合、7日前→6日前→5日前......1日前→今日とデータを通して相関している可能性があります。この間の影響を取り除いて相関を求めたものが偏自己相関と呼ばれます。
この偏自己相関を可視化することによって、後に説明するSARIMAのパラメータ「s」の最適な値を設定する。
# データの自己相関係数を求める
dfg_acf = sm.tsa.stattools.acf(dfg, nlags=50)
dfg_pacf = sm.tsa.stattools.pacf(dfg, nlags=50)
# 自己相関関数(ACF)のグラフを作成する
sm.graphics.tsa.plot_acf(dfg,lags=40)
plt.show()
sm.graphics.tsa.plot_pacf(dfg,lags=40)
plt.show()
青色の影は95%信頼区間です。
この点線の中におさまっていれば自己相関を持たない、つまり現在の自分と過去の自分は関係ないということです。このコレログラムを素直に受け取れば現在と6ヶ月前までは自己相関がある、大きく影響を受けていることがこのグラフからわかります。
 この結果を見て、左から1, 3, 13, ,14, 25, 28, 35, 38, 39, 40番目のデータが影響を与えていることがわかります。
この結果を見て、左から1, 3, 13, ,14, 25, 28, 35, 38, 39, 40番目のデータが影響を与えていることがわかります。
2. 定常性
時間に依らず時系列データの確率分布が変化しないという確率過程の性質を表し、そのような確率過程を定常過程と呼びます。
わかりやすく述べると、時間の経過によらず一定の値を軸に同程度の幅で振れて変化する時系列データは定常性があるといえます。
・定常性が必要な理由
時系列データにおいては定常性がないデータを分析した結果全く意味のない相関(Aが上がればBも上がる、もしくは下がるという関係)を検出してしまう可能性があるからです。時系列データとは時間の経過に沿って変化するデータですから、「時間の経過」という共通項目 が無意味な相関関係を生んでしまうのです。(このような無意味な相関のことを 擬似相関 といいます)
例えば、走行中の車に氷が積まれていたとします。この時、時間が経過するほど車の走行距離は増加し、氷は溶けていきます。しかし、「車がたくさん進んだから、氷が溶けた」というのはナンセンスでしょう。「車が進んだ」と「氷が溶けた」のどちらの事象も、原因は「時間の経過」です。
このような 時系列データの無意味な相関を検出しないため に、定常性のない時系列は階差をとる等の変換を行い定常性のある時系列にしてから分析を進める必要があるのです。
・時系列を定常過程にする方法
ではどうやって定常性を持たせるのでしょうか?
いくつかありますがここでは4つ紹介します。
・対数変換 によって、変動の 分散 を一様にする
・移動平均を取ることによってトレンドを推定した後に、トレンド成分を除去する
・階差系列に変換することでトレンド・季節変動を除去する
・季節調整を利用する
3~6にて詳しく説明いたします。
3. 対数系列
データの変動を穏やかにするのが 対数変換です。
時系列データの中には、値の変動が大きなデータが多くあります。そのようなデータの変動を穏やかにするのが 対数変換です。
4. 移動平均
移動平均とは時系列データのある一定の区間で”平均”をとる、ということを区間を”移動”させながら繰り返すことです。
こうすることで、元のデータの特徴を残しつつ、データを滑らかにすることができます。
例えば月ごとのデータに季節変動がある場合、12個の連続する値の移動平均を求めることで、季節変動を除去することができトレンド成分を抽出することができます。
次に、もとめた移動平均をもとの系列から引き算します。こうすることで系列のトレンド成分を除去することができます。
5. 階差系列
差分をとった後の系列を 階差系列といいます。
時系列データを分析する際、ひとつ前の時間との値の差を扱うことも多いです。このようにひとつ前の値との差をとることを 差分をとる といいます。この様に差分をとった後の系列を 階差系列といいます。
この変換を行うことで原系列の トレンドを取り除く ことができます。
6. 季節調整の利用
1年の周期で周期変動をしていくことを 季節変動 と言いました。 しかし、よくある折れ線グラフではこの季節変動パターンが邪魔をして時系列データのトレンドがわかりにくくなっています。 このような季節変動のあるデータから季節変動以外のデータの動向を探るため、原系列から季節変動を取り除くことが多くあり、そのように季節変動が取り除かれたデータのことを 季節調整済み系列といいます。 StatsModelsのtsa.seasonal_decompose()を用いることで原系列を トレンド 、 季節変動 、 不規則変動(残差) に分けることができ、そのデータをさらに(原系列 - トレンド - 季節変動 = 残差)をおこないます。つまり残差はトレンドと季節変動が取り除かれた定常性のある時系列データになっています。
7. ホワイトノイズ
説明不可能なノイズをホワイトノイズと言います。残差とかとも言います。
時系列モデルにおける不規則変動パターン(誤差)を担います。不規則変動自体は数学的な再現が難しいため、ホワイトノイズを用いるのです。
なかなか聞き慣れない内容でしたが、いかに定常性を持たせるかがポイントのようです。
それでは時系列分析を実際にしていきます。
時系列解析の流れは下記の通りです。
1. データを取得
2. データをグラフにする
3. データの整理
4. モデルの決定
5. SARIMAモデルの実行
1. データを取得
使用するライブラリ
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import datetime
import numpy as np
import itertoolsデータ取得
JNTO日本の観光統計データより
データを取得
# データの読み込みと整理
df = pd.read_csv('CSV_1__2_3__3.csv',thousands=',',encoding="shift-jis",delimiter=",")
df.columns = ['国', '月', '年','訪日数','レート']
df = df.drop(['国',"レート"], axis=1)
d = {'Jan.':'01', 'Feb.':'02', 'Mar.':'03', 'Apr.':'04','May':'05','Jun.':'06','Jul.':'07','Aug.':'08','Sep.':'09','Oct.':'10','Nov.':'11','Dec.':'12'}
df['年月'] = df['年'].astype(str)+ '-' + df['月'].map(d)
df['年月'] = pd.to_datetime(df['年月'])
df = df.drop(['年',"月"], axis=1)
df= df.reindex(['年月', '訪日数'], axis=1)
grouped = df.groupby('年月')
dfg = grouped.sum()
dfg.add_suffix('').reset_index()
#コロナウイルスの影響で訪日数が激減しているため2020年1月以降は消去
dfg= dfg.drop(dfg.iloc[72:].index)
dfg.head()こんな感じのデータ(先頭から5行のみ表示)
年月 訪日数
2014-01-01 944009
2014-02-01 880020
2014-03-01 1050559
2014-04-01 1231471
2014-05-01 1097211
2. データをグラフにする
# データを折れ線グラフで表します
# グラフのタイトルを設定
plt.title("number of foreigners to Japan")
# グラフのx軸とy軸の名前設定
plt.xlabel("date")
plt.ylabel("number_of_foreigners")
# データのプロット
plt.plot(dfg)
plt.show()
3. データの整理
今回使用するデータは、特にかけている部分もなく2014年~2019年までの6年分のデータがあります。機械学習で学習し、2025年までの予測をしていきます。
・自己相関係数
それでは自己相関係数からみていきます。
上記の用語集の際にも記載した内容です。
# データの自己相関係数を求める
dfg_acf = sm.tsa.stattools.acf(dfg, nlags=50)
dfg_pacf = sm.tsa.stattools.pacf(dfg, nlags=50)
# 自己相関関数(ACF)のグラフを作成する
sm.graphics.tsa.plot_acf(dfg,lags=40)
plt.show()
sm.graphics.tsa.plot_pacf(dfg,lags=40)
plt.show()
青色の影は95%信頼区間です。
この点線の中におさまっていれば自己相関を持たない、つまり現在の自分と過去の自分は関係ないということです。このコレログラムを素直に受け取れば現在と6ヶ月前までは自己相関がある、大きく影響を受けていることがこのグラフからわかります。
 この結果を見て、左から1, 3, 13, ,14, 25, 28, 35, 38, 39, 40番目のデータが影響を与えていることがわかります。
この結果を見て、左から1, 3, 13, ,14, 25, 28, 35, 38, 39, 40番目のデータが影響を与えていることがわかります。
・データパターンの確認
sm.tsa.seasonal_decompose()を使用すると原系、トレンド、 季節変動、 残差に簡単に分けることができます。
sm.tsa.seasonal_decompose(dfg, freq=12).plot()
plt.show()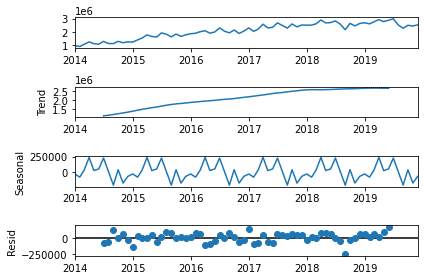
4. モデルの決定
どのモデルで分析、予測していくかを決める必要があります。
今回はSARIMAモデルで行っていきます。
上記のsm.tsa.seasonal_decompose()で取得したデータは上から原系、トレンド、季節性、残差です。
トレンドと季節性があるデータはSARIMAモデルというモデルで表現することができます。
4.2モデルの紹介
・MAモデル
単に時系列が異なる式との間に共通部分を持つために相関性が存在するという性質を持つモデル
・ARモデル
過去の値から回帰的にある時点の値を推定するモデル
・ARMAモデル
ARMAモデル とはその名前の通り後述する ARモデル と MAモデル をあわせたモデルになります。AR(p)のARモデルとMA(q)のMAモデルを組み合わせたときARMA(p,q)のように表すことができます。定常過程にしか適応できません。
・ARIMAモデル
非定常過程の原系列の差分をとり、ARMAモデルを適応したモデルをARIMAモデルという
先程のARMAモデルへ原系列を階差系列に変換し適応したものをARIMAモデルと言います。非定常過程(データの平均や分散が時間に依存している過程)にも適応可能です。d時点前との差分をとった場合のARMA(p,q)で構築したARIMAモデルをARIMA(p,d,q)と表します。
pを自己相関度 モデルが直前 p 個の値を用いて予測されるのか を
dを誘導 時系列データを定常にするために d 次の階差が必要だったこと を
qを 移動平均 モデルが直前 q 個の値に影響を受けること を表しています。
・SARIMAモデル
ARIMAモデルは(p,d,q)をさらに季節周期を持つ時系列データにも拡張できるようにしたモデルです。SARIMAモデルは(p, d, q)のパラメーターに加えて(sp, sd, sq, s)というパラメーターも持ちます。
sp:季節性自己相関
sd:季節性導出,
sq: 季節性移動平均

5. SARIMAモデルの実行
ここで一度SARIMAモデルを用いた時系列データの分析手順をまとめてみましょう。
1.データの読み込み
2.データの整理
3.データの可視化
4.データの周期の把握 (パラメーターsの決定)
5.s以外のパラメーターの決定
6.モデルの構築
7.データとの予測とその可視化
4まで完了しておりますので、5を実行していきます。
(p, d, q)(sp, sd, sq, s)の7つのパラメーターを決めますが、自動で最も適切にしてくれる機能はありません。
そこで情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを書かなければなりません。情報量規準については今回は深く触れませんが、BICの場合は この値が低ければ低いほどパラメーターの値は適切である と理解しておいてください。
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# 周期を埋めて最適なパラメーターを求めてください
selectparameter(dfg, s= 12)[(0, 1, 1), (0, 1, 1, 12), 1548.798013925754]
最適な(p,d,q),(sp,sd,sq,s)(p,d,q),(sp,sd,sq,s)が分かったらいよいよモデルを構築します。モデルの構築にはsm.tsa.statespace.SARIMAX(DATA,order=(p, d, q),seasonal_order=(sp, sd, sq, s)).fit()を用います。
SARIMA_numberof_foreigner = sm.tsa.statespace.SARIMAX(dfg, order=(0,1,1),seasonal_order=(0,1,1,12)).fit()
#構築したSARIMAモデルのBICを出力します
print(SARIMA_numberof_foreigner.bic)1548.798013925754
pred = SARIMA_numberof_foreigner.predict("2016-01-01","2024-12-01")
plt.plot(pred)
plt.show()
予測データだけを出力するのではなく、もとの時系列データと予測データを同時に出力して予測が正しいか確認してみる。(赤色が予測)
plt.plot(dfg)
plt.plot(pred, color="r")
plt.show()
比較的、実数に沿った良いモデルではないかと思います。
モデルができたところで、
今回の目的の、”もしもコロナがなかったら。。。”を比較してみます。
最初に作った、外国人訪日人数、実数値のデータフレームと
今回作成したモデルを表にします。
predict = pd.DataFrame(data = pred[36:60], columns =["訪日数"])
comp = pd.merge(dfg,predict, left_on="年月", right_index=True, how="outer")
comp.columns= ["コロナ禍","予測(コロナがなかったら)"]
print(comp)
コロナ禍 予測(コロナがなかったら)
年月
2019-01-01 2689339 2.648815e+06
2019-02-01 2604322 2.634804e+06
2019-03-01 2760136 2.729270e+06
2019-04-01 2926685 3.044867e+06
2019-05-01 2773091 2.737018e+06
2019-06-01 2880041 2.795494e+06
2019-07-01 2991189 3.026964e+06
2019-08-01 2520134 2.762554e+06
2019-09-01 2272883 2.251114e+06
2019-10-01 2496568 2.696998e+06
2019-11-01 2441274 2.372525e+06
2019-12-01 2526387 2.588380e+06
2020-01-01 2661022 2.601859e+06
2020-02-01 1085147 2.528379e+06
2020-03-01 193658 2.673498e+06
2020-04-01 2917 2.872965e+06
2020-05-01 1663 2.699145e+06
2020-06-01 2565 2.787988e+06
2020-07-01 3782 2.916138e+06
2020-08-01 8658 2.503334e+06
2020-09-01 13684 2.227866e+06
2020-10-01 27386 2.504517e+06
2020-11-01 56673 2.412998e+06
2020-12-01 58673 2.520296e+06わかりにくいのでこういう時は表にします。
x = comp.index
y1 = comp["コロナ禍"]
y2 = comp["予測(コロナがなかったら)"]
plt.figure(figsize=(20,10))
plt.title("Number of foreigners to Japan",fontsize=30)
plt.xlabel("Date",fontsize=20)
plt.ylabel("Numbers(In Millions)",fontsize=30)
plt.grid(True)
plt.plot(x,y1, color="b",label="REAL")
plt.plot(x,y2, color="r",label="NO COVIT19")
plt.legend()
plt.show()
赤色が今回行ったモデル。青色が実数です。
当たり前ですが、コロナウイルスの影響で訪日外国人者数は0に近い状況です。”もしもコロナがなかったら。。。” と思いたくなる本当に深刻な状況であることは訪日数を見るだけでも理解ができるかと思います。
最後に
こうして実際にデータを使って分析することは本当に良い経験になります。
学んだことをアウトプットをすることにより記憶に定着する。
他の方はどのようにしているのか、参考にしながら自分の知識が増える。
本当に正しい情報なのかを確認すること再度復習ができる。
どうやって文字を書けば読みやすいのか、というデータ分析以外の大切な部分も自分で試行錯誤してより良いものを作れる。
まだまだ、初心者レベルですが日々レベルアップできるように楽しんでいければと思います。
最後までお読み頂き本当にありがとうございました。
