ボストンの住宅価格を回帰分析で予測モデルを作ってみた

貴重なお時間をありがとうございます。

今回は機械学習、教師あり学習の回帰分析の復習を兼ねてアウトプットしたいと思います。

回帰分析を行うにあたり、学習し、参考にしたものは、下記の２つです。
・Aidemy Premium 教師あり学習（回帰）コース （オンラインコース）
・【第２版】Python機械学習プログラミング　達人データサイエンティストによる理論と実践（書籍）
使い分けとしては、Aidemyの方で実際に手を動かし実装を行い、
学んだ内容の理論を書籍にて再度復習するような形で使用しております。

目的

今回の目的は、
「ボストン住宅価格データセットをを使って、機械学習アルゴリズムを実装し、"より良い"回帰分析モデルを作ること」です。

早速いきましょう！

そもそも機械学習とは？
機械学習とは
過去のデータをもとに未来を予測するモデルを作ることです。

機械学習の手法は大きく分けると次の3つに分類できます。
・教師あり学習
・教師なし学習
・強化学習
教師あり学習は蓄積されたデータとそれに対応する正解データの組を使って機械が学習を行い、新しいデータや未来のデータの予測、あるいは分類を行う手法です。株価の予測や画像識別などが当てはまります。
さらに、教師あり学習は次の2つの手法に大別されます。
・回帰
・分類
回帰問題で予測される値は株価や宝石の時価などの連続値です。
今回はこの「回帰」を行い、解説してきます。

用語集

分析に行く前にここで教師あり学習、回帰分析を行うにあたり抑えておかないといけないこと、いくつか考え方を紹介します。少し長くなりますが、回帰分析を行うにあたり、必ず抑えておかないといけない内容かと思いますので説明していきます。

1. 線形回帰
 - 線形単回帰
 - 線形重回帰
2. 説明変数、目的変数
3. モデル性能
 - 決定係数
 - 平均二乗誤差（MSE）
- 残差プロット
- 過学習
 - 汎化、正則化

1. 線形回帰

線形回帰は予測するデータの値（数値）を関数を用いて予測する方法です。
回帰分析は、予測したいデータをすでにわかっているデータの関係性を元に推定するアプローチです。特に数値を予測する時に「回帰」と呼びます。
例えば毎分一定量の水が溜まるタンクがあったとします。2分後には8L、4分後には16L溜まりました。5分後にはどれくらいタンクに水量が溜まっているでしょうか。
・予測したい数値：5分後に溜まっている水量 ・すでに分かっているデータ：2分後には8L、4分後には16L溜まるになります。
このように回帰ではすでに分かっているデータの関係性(V = 4t)を元に、予測したいデータ（5分後に溜まっている水量）を推定します。

上記図Aidemyより

- 線形単回帰
1つの予測したいデータ(ex. 水の量)を1つのデータ(ex. 時間)から求める回帰分析です。主にデータの関係性を調べるときに用いられます。

- 線形重回帰
予測したいデータが1つ(ex.レストランの満足度の点数)に対し、予測に用いるデータが複数個(ex. 食べ物のおいしさの点数と接客の良さの点数)ある回帰分析です。すでにある学習データに対して一番誤差が少なくなるように
予測が行われます。

2. 説明変数、目的変数
予測する対象(ex.レストランの満足度)を目的変数と呼び,
説明変数は、目的変数を予測するために用いるデータ(ex. 食べ物のおいしさの点数と接客の良さの点数)です。

3. モデル性能
上記で述べた通り、説明変数を用いて、目的変数を予測するモデルを構築してきます。その作ったモデルの性能を数値化し、”良いモデル”なのか、”良くない”モデルなのか、モデルの性能を数値化できる方法がありあます。 

- 決定係数
予測データと実際の正解データが、どのくらい一致しているかを示す指標です。決定係数R2(2乗)は、正解データ内のばらつきに対して予測値のずれが小さいほど、値が大きくなります。決定係数は1以下の値を取り、おおよそ0.8以上の数値であれば、精度よく予測ができていると言えます。

 - 平均二乗誤差（MSE）
実際の値と予測値の絶対値の 2 乗を平均したものです。
平均二乗誤差 (MSE)では、値が小さいほど誤差の少ないモデルと言えます。
MSEは”Mean Squared Error”の略です。

-残差プロット
実際の値と予測された値の差を表にプロットすること。
そうすることで、外れ値を検出できたり、誤差がランダムに分布されているかチェックすることができる。

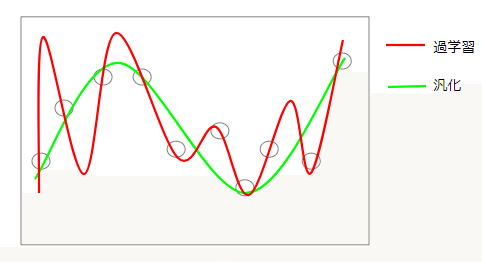
- 過学習
回帰分析の目的は、過去のデータからモデルを学習し、未知のデータを予測することです。しかし、過去のデータは上限があり値段の変動等における事象を完全に説明しているわけではありません。つまり過去のデータに適合しすぎると、データの予測がうまくいかない場合があります。
これを 過学習と呼び、予測精度が下がってしまう原因となります。

- 汎化 、正則化

汎化
過学習を防ぐために取られるアプローチが 汎化です。汎化を意識したモデルを作ることで、学習に使ったデータに適合しすぎず、一般的なケースに対応できるようになります。過学習をすると学習データ（下記(〇)）に過度に適合するので未知のデータの予測がうまくいきません。
そこで汎化を施し、未知のデータに適合するようパラメータを調整する。

上記図Aidemyより

正則化
 汎化の手法として正則化が用いられます。 正則化とは、回帰分析を行うモデルに対し、モデルが推定したデータ同士の関係性の複雑さに対してペナルティを加え、モデルが推定するデータ同士の関係性を一般化しようとするアプローチです。

ポイントは、シンプルに
より良いモデルをいかに作成できるかということです。

とはいうものの、
データが複雑になればなる程、難易度は上がります。
しかし、Pythonの機械学習ライブラリのscikit-learnを使用することで
非常に難しい計算を行ってくれます。

scikit-learnについて

scikit-learn（サイキット・ラーン）はオープンソース（BSD license）で公開されており、個人／商用問わず、誰でも無料で利用することができます。多くの機械学習アルゴリズムが実装されていますが、scikit-learnでは、どのアルゴリズムでも同じような書き方で利用することができます。これから、回帰分析を行うにあたり、実際に使用していきます。




前置きが非常に長くなってしまいましたが、
今回の目的、
「ボストン住宅価格データセットをを使って、機械学習アルゴリズムを実装し、"より良い"回帰分析モデルを作ること」
を行っていきます。
流れは下記の通りです。

1. データを取得、クレンジング
2.データを可視化する
3. 単回帰分析
4. 重回帰分析
5. モデルの性能評価
6. モデルの改善

まずは今回扱うデータの内容です。

1. データを取得、クレンジング
使用するライブラリ

import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
%matplotlib inline

1. ボストンの住宅価格のtoyデータを取得。
2. データフレームにし、カラムを割り当てる。
3. 目的変数（PRICE）を追加しデータフレームの最初の５行をを確認。

#1
from sklearn.datasets import load_boston
boston=load_boston()

#2
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df.head()

#3
df['PRICE'] = pd.DataFrame(boston.target)
df.head()

#2

#3

目的変数PRICEが一番右端に加わったのがわかります。

2.データを可視化する

格変数間の散布図行列を作成し、データの分布や外れ値が含まれているかどうか見てみる。ここではINDUS、NOX、RM、TAX、PTRATIO、LSTAT、PRICEに絞って見ていきます。

import seaborn as sns
cols = ['INDUS','NOX','RM','TAX','PTRATIO','LSTAT','PRICE']
sns.pairplot(df[cols], size = 2.5)
plt.tight_layout()
plt.show()     

RMとPRICEの関係が線形であることや、
PRICEのヒストグラム（右下）が正規分布に見えるが外れ値が含まれることも見て取れます。

次に相関行列を用いて、格変数間の関係を数値で確認してみます。
相関行列とは従属関係を数値化するピアソンの積率相関係数を成分とする正方行列です。相関係数の範囲は−１から１です。１の場合は正の相関関係があり、−１の場合は反対に負の相関関係があり、０は相関関係がありません。
seabornのheatmap使用すると、一目で確認できます。

cols = ['INDUS','NOX','RM','TAX','PTRATIO','LSTAT','PRICE']
df['PRICE'] = pd.DataFrame(boston.target)
plt.figure(figsize=(13, 13))
cm = np.corrcoef(df[cols].values.T)
hm = sns.heatmap(cm,
                cbar= True,
                annot = True,
                square = True,
                fmt = '.2f',
                annot_kws={'size':15},
                yticklabels=cols,
                xticklabels=cols
                )
              
            
plt.tight_layout()
plt.show()

LSTATとPRICEが強い負の相関関係がありそうですが、先ほど確認した散布図で、非線形の相関関係があることが見て取れます。
RMとPRICEは0.7とこちらは正の相関関係があり、散布図からも線形関係があると見て取れます。RMは単回帰分析をするのに適していると考えられるため、実際にRMとPRICEを使用し単回帰分析を行ってみます。

3. 単回帰分析

最初に使う線形回帰モデルはscikit-learnにあるLinearRegressionです。
LinearRegressionのメリットは標準化されていない変数にもうまく順応してくれます。
説明変数（RM）をX、目的変数（PRICE）をYに格納し、単回帰分析を行います。

from sklearn.linear_model import LinearRegression
X = df[['RM']].values
Y = df["PRICE"].values

model = LinearRegression()

model.fit(X,Y)　　　#fitで指定したモデルで学習を行う
y_pred = model.predict(X)　　　#predictで予測を行う

print('傾き： ' , model.coef_)
print('切片： ' ,  model.intercept_)

出力
傾き： [9.10210898]
切片： -34.67062077643857

学習と、予測を行なったモデルをグラフにし可視化を行う。

#定義
def lin_regplot(X,Y,model):
   plt.scatter(X,Y,c ='blue',edgecolor= 'white',s= 70)
   plt.plot(X,model.predict(X),color='black',lw=2)
   return

lin_regplot(X,Y,model)
plt.show()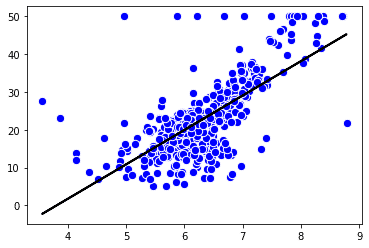

LinearRegressionを使用することで線形単回帰ができ、部屋数が上がるにつれて価格も上がることがグラフから読み取れます。
ただ、こちらのモデルでは、上部に外れ値が多く確認でき、外れ値に左右されてしまっているかと思います。
場合によってはデータのほんの一部がモデルの推定に大きな影響を与えることがあります。
このような外れ値を取り除きたい時に変わる方法を一つ紹介します。

RANSACを使用したロバスト回帰モデル

一言で言うと、正常値（外れ値ではないもの）を学習させるアルゴリズム。RANSACアルゴリズムの反復処理は下記の５つです。
1. 正常値としてランダムな数のサンプルを選択し、モデルを学習。
2. 学習済みのモデルに対して、その他全てのデータ点を評価し、ユーザー指定の許容範囲となるデータを正常値に追加する。 
3. 全ての正常値を使ってモデルを再び学習。
4. 正常値に対する学習済みのモデルの誤差を推定する。
5. モデルの性能がユーザー指定のしきい値の条件を満たしている場合、またはイテレーションが規定の回数に達した場合はアルゴリズムを終了する。そうでなければ、１に戻る。

実際にコードを書いてみます。

from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(),
                        max_trials =100,         ＃イテレーションの最大数
                        min_samples=50,　　　　　　＃ランダムに選択されるサンプルの最小数を５０に
                        loss = 'absolute_loss',  #学習直線に対するサンプル点の縦の距離の絶対値を計算
                        residual_threshold =5.0, ＃学習直線に対する縦の距離が５単位距離ないの点のみを正常値に含む
                        random_state=0)
ransac.fit(X,Y)

inlier_mask = ransac.inlier_mask_　                    #正常値を表す真偽値を取得
outlier_mask = np.logical_not(inlier_mask)           　#外れ値を表す真偽値を取得
line_x = np.arange(3, 10 ,1)　　　　　　　　　　　　　　　　#３から９までの整数値を作成
line_y_ransac = ransac.predict(line_x[:, np.newaxis])　#予測値を計算
plt.scatter(X[inlier_mask],Y[inlier_mask],
          c='steelblue',edgecolor= 'white', marker= 'o', label='Inliers')
plt.scatter(X[outlier_mask],Y[outlier_mask],
          c='limegreen',edgecolor= 'white', marker= 's', label='Outliers')

plt.plot(line_x, line_y_ransac, color ='black', lw =2)
plt.xlabel('RM')
plt.ylabel('PRICE')
plt.legend(loc='upper left')
plt.show()

print('傾き： ' , ransac.estimator_.coef_)
print('切片： ' ,  ransac.estimator_.intercept_)​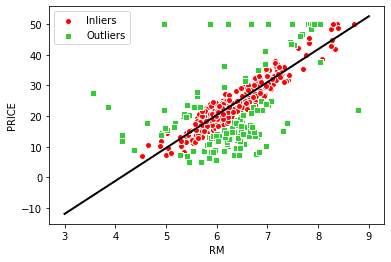

傾き： [10.73450881]
切片： -44.08906428639813

RANSACを使用すると、未知のデータの予測にプラスに働くかどうかはデータ次第でわからないですが、データセットの外れ値の影響は抑えられます。

4. 重回帰分析
重回帰分析も単回帰分析と同様、scikit-learnのLinearRegressionを使用します。
今回は重回帰なので全ての変数をXに、目的変数（PRICE）をYに格納します。

# 目的変数のみ削除して変数Xに格納
X = df.drop("PRICE", axis=1)
# 目的変数のみ抽出して変数Yに格納
Y = df["PRICE"]

まずは、どの説明変数が、目的変数PRICEに影響を与えているのか、回帰係数を算出してきます。

model = LinearRegression()
model.fit(X,Y)　　#fitでモデルの当てはめ
model.coef_　　　 #coef_で偏回帰係数を算出 

＃＃抽出データ
array([-1.08011358e-01,  4.64204584e-02,  2.05586264e-02,  2.68673382e+00,
      -1.77666112e+01,  3.80986521e+00,  6.92224640e-04, -1.47556685e+00,
       3.06049479e-01, -1.23345939e-02, -9.52747232e-01,  9.31168327e-03,
      -5.24758378e-01])

たったこれだけで、回帰係数算出してくれます。
しかし、これで取得できるのは上記のようなデータなので、見やすくするため、ヒートマップを作成し、可視化をしてみます。

import seaborn as sns
cols = ['PRICE']
cm = df_coefficient
plt.figure(figsize=(3, 7))
hm = sns.heatmap(cm,
                cbar= True,
                annot = True,
                square = True,
                fmt = '.2f',
                annot_kws={'size':13},
                yticklabels=df.columns,
                xticklabels=cols
                )
  
             
plt.tight_layout()
plt.show()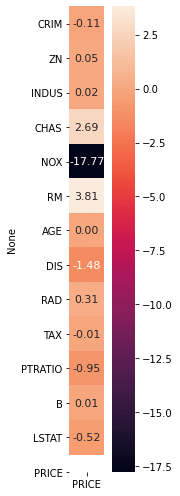

RM（部屋数）が価格の上昇に貢献し、
NOX（一酸化炭素濃度）が価格を下げる要因にしていることが見て取れます。

5. モデルの性能評価
モデルの性能を偏りなく推定する方法は、今あるデータをトレーニングデータとテストデータに分け、トレーニングデータでモデルを作り、テストデータでモデルをテストすることが必要です。
実際にコードを書いていきます。

from sklearn.model_selection import train_test_split
X = df.drop("PRICE", axis=1)
Y = df["PRICE"]

X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size=0.3, random_state=0)
model= LinearRegression()
model.fit(X_train, y_train)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)

トレーニングに使用するデータを７割、テストに使用するデータを３割に分けて学習をさせます。

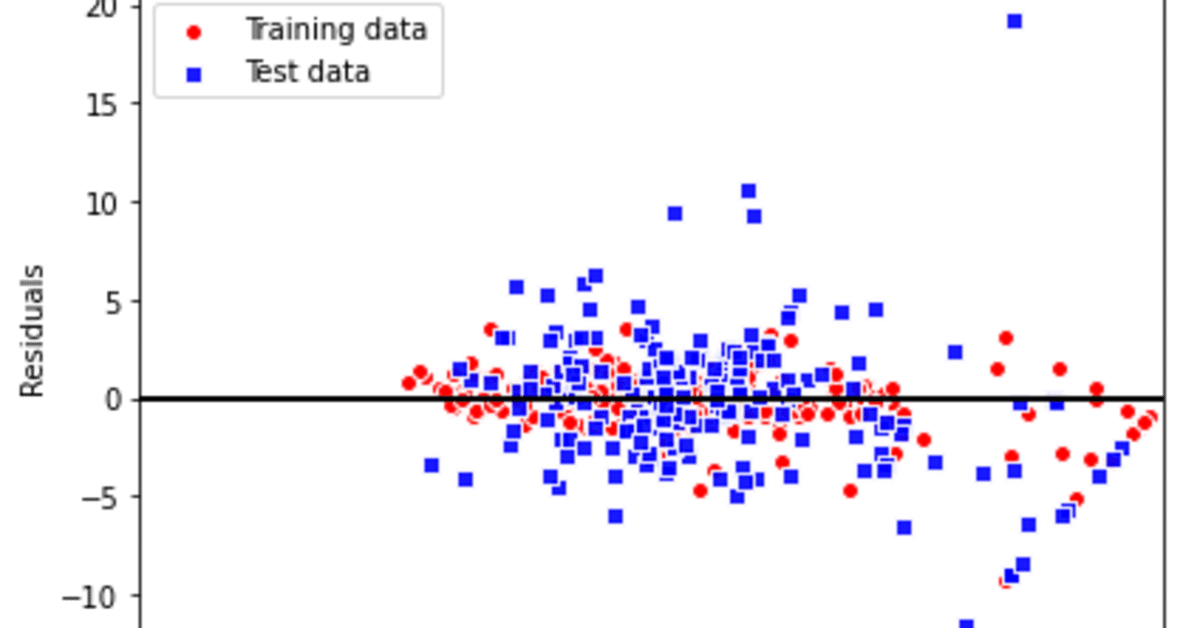
- 残差プロット
用語集でも触れましたが、
この線形回帰モデルを診断するために、実数値と予測された値のさをプロットして比較します。非線型性や、外れ値を検出できます。

plt.figure(figsize = (8,4)) #プロットのサイズ指定

plt.scatter(y_train_pred, y_train_pred - y_train,
                  c = 'red', marker = 'o', edgecolors='white',
                  label = 'Training data')
plt.scatter(y_test_pred, y_test_pred - y_test,
                  c = 'blue', marker='s', edgecolors='white',
                  label = 'Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10,xmax=50,color='black', lw=2)

plt.tight_layout()
plt.show()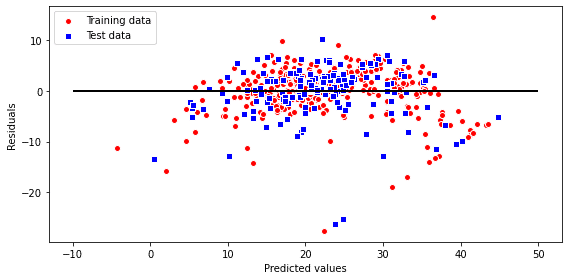

予測が完璧であれば、残差は０になり散らばりがないですが、そのようなことは実際にはありえないですし、よいモデルとも言えません。良いモデルとは誤差がランダムに分布て、残差が直線付近に散らばっています。今回の右下の斜めに等間隔でプロットされている点は、おそらく何らかのデータの情報設定によって起こっているものだと思われます。

- 平均二乗誤差

平均二乗誤差とは、実際の値と予測値の絶対値の 2 乗を平均したものです。
平均二乗誤差 (MSE)では、値が小さいほど誤差の少ないモデルと言えます。簡単に求めることができます。

from sklearn.metrics import mean_squared_error

print("trainData", mean_squared_error(y_train,y_train_pred))
print("testData", mean_squared_error(y_test,y_test_pred))

trainData 19.958219814238046
testData 27.195965766883365

トレーニングデータに比べテストデータが今回のようにかなり大きいですが、この場合は、トレーニングデータの過学習を起こしている可能性が高いです。

- 決定係数
正解データ内のばらつきに対して予測値のずれが小さいほど、値が大きくなります。決定係数は1以下の値を取り、おおよそ0.8以上の数値であれば、精度よく予測ができていると言えます。

from sklearn.metrics import r2_score
print("決定係数trainData", r2_score(y_train,y_train_pred))
print("決定係数testData", r2_score(y_test,y_test_pred))

決定係数trainData 0.7645451026942549
決定係数testData 0.6733825506400176

トレーニングデータセットでは比較的良い決定係数ですが、テストデータセットはいまいちな結果となってしまっております。

6. モデルの改善
今回の目的である、「より良いモデルを作ること」を行うためにはここからが重要です。トライしていきます。まずは、重要なポイントを説明致します。

- 正則化
それでは、過学習を起こしてしまっているモデルの対処方法として、正則化の説明致します。用語集でもお伝えした通り、正則化かは過学習の問題に対処する１つの手法です。
正則化にはL1正則化とL2正則化が多く用いられます。

L1正則化
「予測に影響を及ぼしにくいデータ」にかかる係数をゼロに近づける手法です。主に余分な情報がたくさん存在するようなデータの回帰分析を行う際に用います。また、特徴量削減の手法として用いることもできます。

L2正則化
係数が大きくなりすぎないように制限する手法で、過学習を抑えるために用いられます。学習の結果、得られる係数が大きくならないので汎化しやすいという特徴があります。

正則下された線形回帰のもっとも一般的なアプローチを３つ紹介致します。

1. ラッソ回帰
L1正則化を行いながら線形回帰の適切なパラメータを設定する回帰モデルです。L1正則化では、データとして余分な情報がたくさん存在するようなデータの回帰分析を行う際に使用します。そのため、データセットの数（行数）に比べて、パラメータの数（列数）が多い場合には、ラッソ回帰を利用するのが良いでしょう。

2.リッジ回帰
L2正則化を行いながら線形回帰の適切なパラメータを設定する回帰モデルです。リッジ回帰には、汎化しやすいという特徴があります。

3. ElasticNet回帰
ラッソ回帰とリッジ回帰を組み合わせて正則化項を作るモデルとなります。ラッソ回帰で取り扱った余分な情報がたくさん存在するようなデータに対して情報を取捨選択してくれる点と、リッジ回帰で取り扱った 汎化しやすい点が挙げられます。

使用方法は下記にて説明致しますが、LinearRegressionと同じようにsklearn.linear_modelからインポートを行い、利用できます。

それでは実際にコードを書いて実装していきます。

ラッソ回帰

from sklearn.linear_model import Lasso

X = df.drop("PRICE", axis=1)
Y = df["PRICE"]
X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.3, random_state=0)
model2 = Lasso()
model2.fit(X_train, y_train)
lasso_y_train_pred = model2.predict(X_train)
lasso_y_test_pred = model2.predict(X_test)


print("MSE_LASSO_TrainData", mean_squared_error(y_train,lasso_y_train_pred))
print("MSE_LASSO_TestData", mean_squared_error(y_test,lasso_y_test_pred))
print("決定係数LASSO_TrainData:", r2_score(y_train, lasso_y_train_pred))
print("決定係数LASSO_TestData:", r2_score(y_test, lasso_y_test_pred))

MSE_LASSO_TrainData: 24.71652261843586
MSE_LASSO_TestData: 32.34503899856862
決定係数LASSO_TrainData: 0.7084095500978869
決定係数LASSO_TestData: 0.6115433359595555

リッジ回帰

from sklearn.linear_model import Ridge

X = df.drop("PRICE", axis=1)
Y = df["PRICE"]
X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.3, random_state=0)
model1 = Ridge()
model1.fit(X_train, y_train)
ridge_y_train_pred = model1.predict(X_train)
ridge_y_test_pred = model1.predict(X_test)

print("MSE_RIDGE_TrainData: ", mean_squared_error(y_train,ridge_y_train_pred))
print("MSE_RIDGE_TestData: ", mean_squared_error(y_test,ridge_y_test_pred))
print("決定係数RIDGE_TrainData: ", r2_score(y_train, ridge_y_train_pred))
print("決定係数RIDGE_TestData: ", r2_score(y_test, ridge_y_test_pred))

MSE_RIDGE_TrainData: 20.1447936646545
MSE_RIDGE_TestData: 27.762224592166508
決定係数RIDGE_TrainData: 0.7623440182689594
決定係数RIDGE_TestData: 0.6665819091486691

ElasticNet回帰
下記のようにl1_ratioを設定すると、L1正則化とL2正則化の割合を指定できます。l1_ratio=0.3の場合、L1正則化が30％、L2正則化が70％効いていることを示しています。指定しない場合、L1正則化が50%、L2正則化が50%になります。）

from sklearn.linear_model import ElasticNet
X = df.drop("PRICE", axis=1)
Y = df["PRICE"]
X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.3, random_state=0)
model3 = ElasticNet(l1_ratio=0.3)
model3.fit(X_train,y_train)
elastic_y_train_pred = model3.predict(X_train)
elastic_y_test_pred = model3.predict(X_test)


print("MSE_ElasticNET_TrainData: ", mean_squared_error(y_train,elastic_y_train_pred))
print("MSE_ElasticNET_TestData: ", mean_squared_error(y_test,elastic_y_test_pred))
print("決定係数ElasticNet_TrainData: ", r2_score(y_train, elastic_y_train_pred))
print("決定係数ElasticNet_TestData: ", r2_score(y_test, elastic_y_test_pred))

MSE_ElasticNET_TrainData: 24.30059104166107
MSE_ElasticNET_TestData: 31.735117999517808
決定係数ElasticNet_TrainData: 0.7133164570067816
決定係数ElasticNet_TestData: 0.618868350365319

格モデルのMSEと決定係数を比較してみましょう。

比較するとLinearRegressionがMSEも低く、決定係数も高いことがわかります。今回のデータではうまく適応できませんでしたが、それぞれのメリットを活かしたモデルになったのではないでしょうか。

- ランダムフォレスト回帰
ここまで色々と線形回帰分析手法を見てきましが、最後にランダムフォレスト回帰を見ていきます。
結果を複数のモデルの多数決で決める手法です。複数の簡易分類器を一つの分類器にまとめて学習させる アンサンブル学習と呼ばれる学習の手法でもあります。データセットの外れ値にあまり影響を受けず、パラメータのチューニングをそれほど要求しないというメリットがあります。
詳しい説明はこちらの記事が非常に見やすく説明されておりますのでご覧ください。

X = df.drop("PRICE", axis=1)
Y = df["PRICE"]
X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size=0.4, random_state=1)

from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
                            criterion = 'mse',
                            random_state=1,
                            n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)

print("trainData", mean_squared_error(y_train,y_train_pred))
print("testData", mean_squared_error(y_test,y_test_pred))

print("決定係数trainData", r2_score(y_train,y_train_pred))
print("決定係数testData", r2_score(y_test,y_test_pred))

trainData 1.643622704224367
testData 11.085384101576372
決定係数trainData 0.9794626907930438
決定係数testData 0.8772555925989014

トレーニングデータを過学習してしまうことがわかりました。
しかし、決定係数はかなり高い数値になり、うまく目的変数と説明変数の関係を説明できています。
最後に残差を見てみましょう。

plt.scatter(y_train_pred,
           y_train_pred - y_train,
           c = 'red', 
           marker = 'o', 
           edgecolors='white',       
           label = 'Training data')
plt.scatter(y_test_pred, 
           y_test_pred - y_test,
           c = 'blue', 
           marker='s',
           s= 35,
           edgecolors='white',
           alpha=0.9,
           label = 'Test data')
plt.xlabel('predicted vales')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin= -10,xmax=50,lw=2, color='black')
plt.xlim([-10,50])
plt.tight_layout()
plt.show()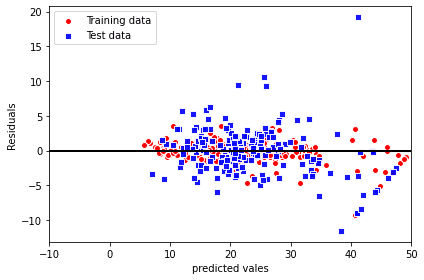

決定係数に表されているように、テストデータよりもトレーニングデータの方に適合されています。
ただ、線形回帰モデルの残差プロットをしたものと比べると、大きく改善されてきています。


- 今回の回帰分析を通して

今回の目的は
「機械学習アルゴリズムを実装し、"より良い"回帰分析モデルを作ること」でした。
"より良い"モデルはできましたが、完璧なモデルの構築はできませんでした。
予測値と説明変数の情報に関連性がなかったり、予測値の誤差にパターンがある場合は、残差プロットに予測値の情報が含まれしまい、そうした説明情報が残差にでてしまうことがあるようです。
そういったことに対処するためのアプローチは存在せず、実験が必要で、学習アルゴリズムのはいパラメータをチューニングして良いモデルを作るために改善を続けることが重要であるようです。

- 最後に
最後までご一読本当にありがとうございます！

学んだ内容をアウトプットすることは本当に本当に学びが多く驚きます。
他の方の記事を参考にしたり、書籍を精読したり、新しいモデル構築にチャレンジしたりと良いことしかないです。

次回の目標は時間を区切り、シンプルな良いアウトプットを出すことです。
どうしても記事にすると間違えてはいけないといった感情が入り、調べる時間が増えてしまったり、途中から内容を増やしてしまい、かえって理解しづらくなってしまっています。
Simplicity is not simple.
本当に理解しているからこそ、シンプルで洗練された内容になると思います。そこを目指してこれからもアップしていきます。