
DWSIM:ヒートポンプ
DWSIMでヒートポンプを模擬してみました。
水道水を井戸水を利用して温水にすることを例として考えてみました。
DWSIM v6.4.6
DWSIMの紹介は、以下になります。
検討状況
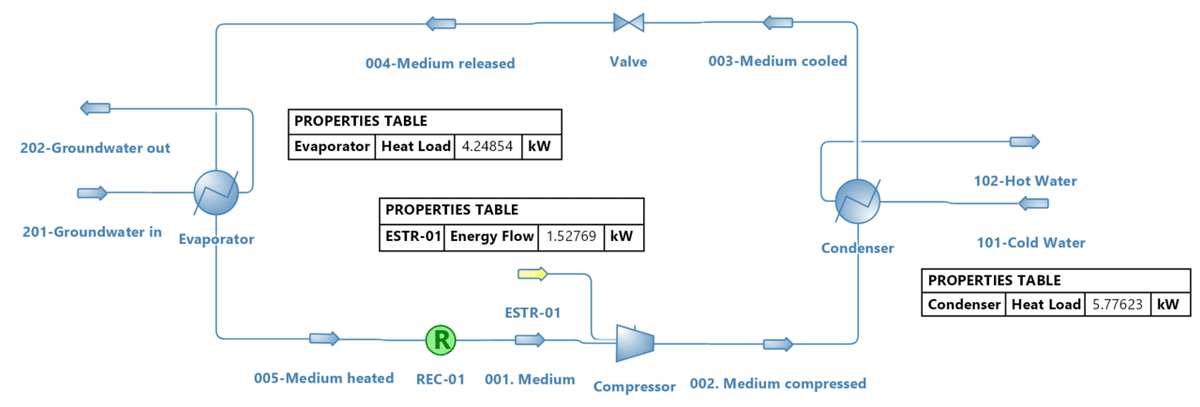
以下のような装置をイメージしています。(流れのみです。機械、ハードの詳細は未検討です。)

地下水は、豊富にあるとします。地下水の温度は、25℃、水道水も25℃としました。
熱を組み上げてくる媒体は、イソブタンを選びました。(操作域で液化、気化などがうまくいくものを選ぶ。エアコンの冷媒などがよいですが、シミュレーターに十分な物性があるものを優先して選んでいます。)
媒体の流れは、①蒸発器で熱をもらい気化し、②コンプレッサーで昇圧(仕事をされる)③凝縮器(熱交換器)で水道水に熱を渡して液化、④減圧弁で圧力を低下、断熱膨張、①にもどり蒸発器で熱をもらい気化、というサイクルを繰り返す。
101は、市水の入り、102は、温められたもの、
201は、地下水の流入、202は、熱をとられたあとの地下水の流出
としました。
DWSIMの設定
以下は、今回の問題のDWSIMでの設定ファイルです。(自己責任で取り扱いをお願いします。)
内容についての説明です。
Compounds(物質):水、イソブタン(Isobutane)
Property Packages:Peng-Robinson EOS (実在気体の状態方程式の一つ)
Flowsheetは、以下の様に作っています。

001 ~ 005が媒体が流れているStreamになります。プロセスシミュレーターでは、閉ループ(リサイクルループ)があるときには、それを明示する必要があります。REC-01がその役割になります。計算を収束させるためには、初期値の設定も重要になります。001と005は同じになるはずです。
流量の起点として、Stream 101、上水を100kg/hrで流すことにしました。お風呂が200L程度と思いますので、その半分を1時間で流すイメージです。
それに対して、媒体(イソブタン)は、50kg/hrで回すことにしました。(計算しながら調整としました。)
コンプレッサーは、出口媒体圧力を 700kPa、効率を75%とし、減圧弁は、出口媒体圧力を101.3kPa(常圧)としました。
Condensorの条件は、媒体の熱交換後の温度を35℃、Evaporatorの条件は、熱交換後の媒体の温度を20℃で設定しました。
計算結果
計算結果は以下のようになります。

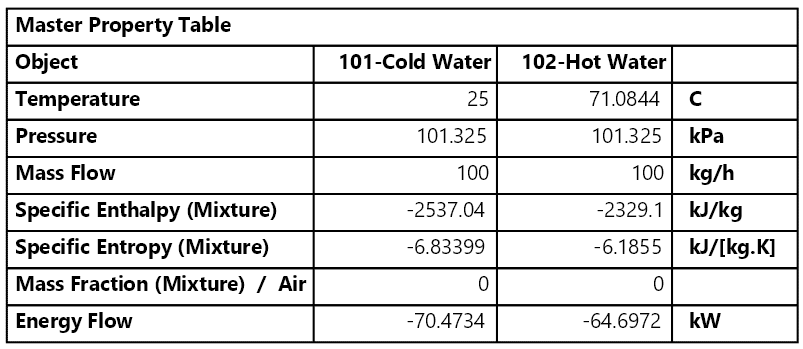

水は、71℃まで温められます。地下水は豊富に流れているとして3500kg/hrとしました(温度低下が5℃程度のなるように恣意的調整しました)。
コンプレッサーの動力は、1.53kWで、温水を作るのに必要なエネルギーは、5.78kWでした。差の4.25kWは地下水の熱を組み上げて達成しています。
1.53kWの動力で、低温熱源(地下水)を利用することで、5.78kWの加熱が達成できていることになります。動力3.78倍の熱となっています。
200kg(200L)、87℃のお湯をこのシステムで作ったとすると、1.53kWで2時間かかるので、20円/kWhの電力単価すると、40円でできることになる。
エアコンなどは、このような原理で、必要な熱(冷熱)に対して省エネルギーを達成しています。
PH図上では、以下のようになります。

まとめ
ヒートポンプをプロセスシミュレーターで模擬してみました。
ヒートポンプで熱源から熱を組み上げると動力以上の熱を利用することができる予想です。。
所感
媒体は、シミュレーターに物性がそろっており、ちょうどよい温度域で気化、凝縮できるものを選んだ。実際は、不燃性などの特徴も踏まえてハロゲン化物や、アンモニアなどが使われているようだ。(環境問題でつかわれなくなったものなど、ここはエアコンメーカーの方や、冷媒メーカーの方が詳しいと思う。私はそこまで専門ではない。)
今回の問題を掘り下げていくと熱交換器のサイジング、弁のサイジングなど検討課題がある。
PH図など、シミュレーターで書く方法も整理していきたいとおもう。
熱力学の問題としてヒートポンプは面白いと思って記載してみた。
例えば、常時廃熱がある機器などで環境の悪化(作業場が暑くなる)などがあればその排熱を熱源としてくみ上げてより高い温度として有効利用できるかもしれない。
参考文献
J. M. Smith, H. C. Van Ness, M. M. Abbott, Introduction to Chemical Engineering Thermodynamics 7th, McGraw-Hill, 2005, P.317 - P.326
化学工学会 編、伊東 章 著、例題で学ぶ化学プロセスシミュレータ フリーシミュレータ COCO/ChemSepとExcelによる解法、コロナ社、P.65
いいなと思ったら応援しよう!

