Python : 常微分方程式
odeint, BDFの利用について
Stiff な方程式なのか、うまく解けなかったときのメモです。
連続槽型反応器の濃度変化をグラフ化したく、常微分方程式を数値的に解くことを考えました。
問題
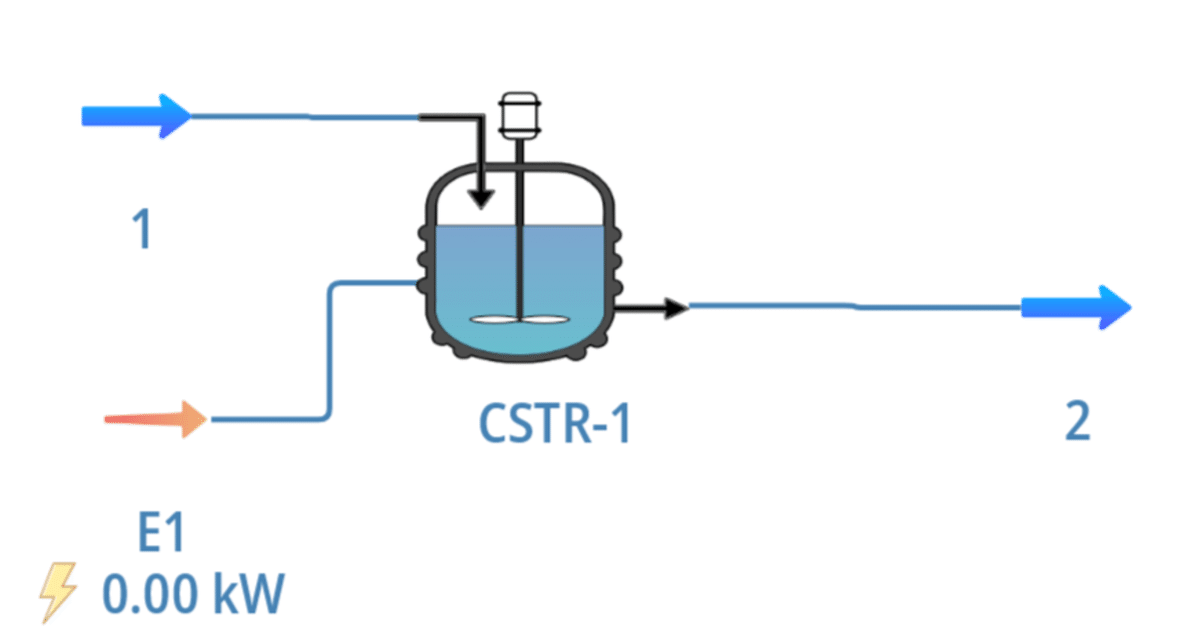
反応器サイズ 1L のCSTRに、反応速度式 $${-r_A = k C_A^{1.558}}$$となる原料を 100mmol/Lの濃度で、流量 10, 3, 1.2, 0.5 L/hrの各流量変化させて供給した。各流量切り替え前には、タンク内の反応成分は押し出して、ゼロの状態からスタートする。各流量におけるタンクの濃度変化を確認する。
$$
{ V\frac{dC}{dt} = QC_{A0} - QC_{A} - kC_{A}^n }
$$
以下、計算条件
$${V = 1 [L] \\ Q = (10, 3.0, 1.2, 0.5) [L/hr] \\ k = 0.1397 [(L/mol)^{0.558} / hr] \\ n = 1.558 \\ C_{A0} = 100.0 [mmol/L] }$$
計算
odeint での計算
python scipy にあるodeint でまずは解いてみました。
pythonのodeintに渡す関数の引数の中の並びが標準では、$${(y, t)}$$ で、他のソフトでは、$${ (t, y) }$$ の方が多いかなと思い、tfirst オプションをtrueにして後者になるようにしています。
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.integrate import odeint
plt.rcParams['figure.figsize'] = (8,8)
plt.rcParams['font.size'] = 22
# モデル式の定義
def rA(t, CA, k,n,Q):
if t < 0.5:
CA0 = 0.0
else:
CA0 = 100
dCA_dt = (Q*CA0 - Q*CA - k * CA**n) / V #
return dCA_dt
V = 1.0 # L
k = 0.1397 # [(L/mol)^0.558/ hr]
n = 1.558 #
CA0 = 100.0 # mmol/L
time = np.linspace(0, 5, 101)
i = 0 # run No.
for Q in np.array([10.0, 3.0, 1.2, 0.5]):
CA = odeint(rA,0, time, args=(k,n,Q), tfirst=True)
i = i + 1
plt.plot(time, CA, label='Run '+ str(i) + ' Q=' + str(Q) + '[L/hr]')
plt.plot([0,0.5,0.5,5],[0,0,100,100], label='step injection')
plt.grid()
plt.xlabel('time[hr]')
plt.ylabel('Concentraion[mmol/L]')
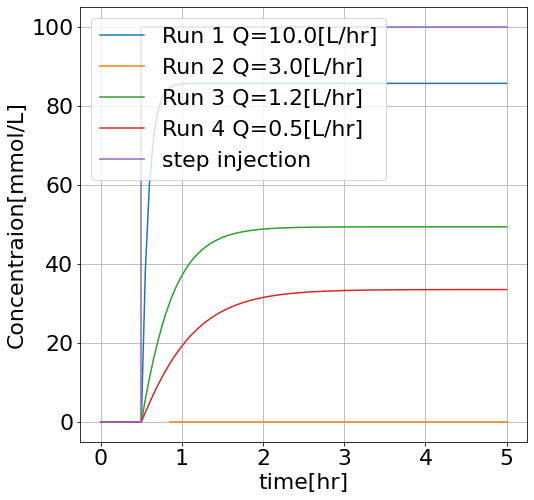
plt.legend()計算結果のグラフです。流量3.0L/hrの時に計算がうまくいかないようです。
scipy.integrate.odeint — SciPy v1.10.0 Manual
Scipyのマニュアルとよむと、lsoda法が使われている。
lsoda法は、Adams法とBDF法を切り替えて使うとのこで、Stiff, nonstiffの両方に対応していそうなのですが、うまくいきませんでした。
BDFでの計算
BDF(陰解法)でのトライに変えてみます。
scipy.integrate.BDF — SciPy v1.10.0 Manual
を使ってみました。
以下に変更しています。
from scipy.integrate import BDFimport numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.integrate import BDF
plt.rcParams['figure.figsize'] = (8,8)
plt.rcParams['font.size'] = 22
V = 1.0 # L
k = 0.1397 # [(L/mol)^0.558/ hr]
n = 1.558 #
CA0 = 100.0 # mmol/L
t_end = 5.0
i = 0
for Q in np.array([10.0, 3.0, 1.2, 0.5]):
def rA(t, CA):
if t < 0.5:
CA0 = 0.0
else:
CA0 = 100
dCA_dt = (Q*CA0 - Q*CA - k * CA**n) / V #
return dCA_dt
# CA = odeint(rA,0, time)
ODE = BDF(rA, t0=0.0, y0=[0.0], t_bound=t_end)
log_t = []
log_CA = []
while ODE.status == 'running':
ODE.step()
log_t.append(ODE.t)
log_CA.append(ODE.y)
i = i + 1
plt.plot(log_t, log_CA, label='Run '+ str(i) + ' v0=' + str(v0)+'L/hr')
#plt.plot(time, CA, linewidth=2, label='Run '+ str(i) + ' v0=' + str(v0))
plt.plot([0,0.5,0.5,5],[0,0,100,100], label='step injection')
plt.grid()
plt.xlabel('time[hr]')
plt.ylabel('Concentraion[mmol/L]')
plt.legend()
うまくいったようです。定常に落ち着く濃度も、問題ないようです。(別途確認しています。)
BDFに渡す常微分方程式内のパラメータを外から渡せないようになるので、for文の中で、反応速度式を毎回定義しなおす形になっています。
まとめ
lsoda法で自動で切り替えてもらうのでは、対応できない事象があることを体験しました。
より一般的な実装になっているode(今回は使っていません)、BDF関数は、使い方が少しわかりにくいですが、慣れれば問題なさそうです。
以上、メモです。
いいなと思ったら応援しよう!

