
Photo by
qoocho_emily
R:中心極限定理のモンテカルロ法による確認
おはこんばんちわ。チャパティです。
今日は「中心極限定理をモンテカルロ法で確認する」というのをやっていこうと思います。
前の記事はこちら
その前に
中心極限定理?モンテカルロ法?
モンテカルロ法は前回の講義に書いてるので、軽くだけ
モンテカルロ法
偶然現象の経過をシミュレーションする場合に、乱数を用いて数値計算を行い、問題の近似解を得る方法。コンピューターの発達によって広い分野で利用されている。
三省堂 大辞林より
中心極限定理とは
辞書的にはこんな感じ。
中心極限定理
母集団分布に関係なく、独立な確率変数の和の確率分布関数は、nが大きくなるにつれて正規分布に収束すること。すなわち、母平均μ、分散μ²の確率分布に従うn個の事象を考えるとき、nが大きくなるとその平均と分散はμとμ²/nの正規分布に近づく
https://bellcurve.jp/statistics/glossary/1440.html
よーするに
標本数を増やすと、標本の分布は正規分布に近づくという定理です。
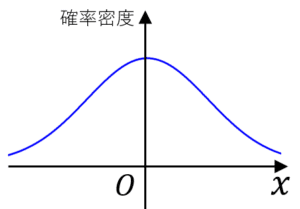
正規分布ってこんなやつね。
では、本題
中心極限定理のモンテカルロ法による確認
準備
XにÜ(0,1)とℬ(0,3)を過程
Ü(0,1)←一様分布…①
ℬ(0,3)←ベルヌーイ分布…②
①のとき、n=2,3,10,100,1000
②のとき、n=3,10,1000,100000
M=1000000(→1000000回でやるべきだけど、パソコン君つらいので1000回でやります。)
とする。
計算方法
1.Xに分布を仮定して、n個の乱数Xi(i=1,2,....,n)を発生させ、乱数値をx₁,x₂,…xnとする
2.平均μ,分散σ²を所与として、
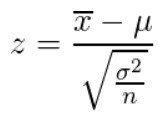
を計算する。
ただし、xの平均=1/n*Σxi
3.1と2をM回繰り返し、M個の系列でヒストグラムを作成
実装!
M <- 1000
n.u <- c(2, 3, 10, 100, 1000)
n.b <- c(3, 10, 1000, 10000, 100000)
a <- seq(-4, 4, 0.01)
b <- dnorm(a)
UNIF <- matrix(0, M, 5 )
BELN <- matrix(0, M, 5 )
p <- 0.3
pdf( file = "中心極限定理.pdf", height = 5, width = 7, family = "Times" )
par( mfrow = c( 5, 2), mar = c( 2, 2, 1.5, 0.5))
for (j in 1:5)
{
for (i in 1:M ) {
x <- runif( n.u[j])
y <- rbinom( n.b[j], 1, p)
z <- ( mean( x ) - 0.5) / sqrt(( 1 / 12 ) / n.u[j] )
w <- ( mean( y ) - p) / sqrt( p * ( 1 - p) / n.b[j])
UNIF[i , j] <- z
BELN[i , j] <- w
}
hist( UNIF[,j], freq = FALSE, xlim = c( -4 , 4), ylim = c(0, 0.5),main = paste("Uniform, n = ", n.u[j], sep = "" ), xlab = "", ylab = "", bty = "n", xaxt = "n", yaxt = "n")
par( new = T )
plot(a, b, xlim = c( -4, 4), ylim = c( 0, 0.5), type = "l", xlab = "" , ylab = "", bty = "n", xaxt = "n", yaxt = "n")
hist( BELN[,j], freq = FALSE, xlim = c( -4 , 4), ylim = c(0, 0.5),main = paste("Bernoulli, n = ", n.u[j], sep = "" ), xlab = "", ylab = "", bty = "n", xaxt = "n", yaxt = "n")
par( new = T )
plot(a, b, xlim = c( -4, 4), ylim = c( 0, 0.5), type = "l", xlab = "" , ylab = "", bty = "n", xaxt = "n", yaxt = "n")
}
dev.off( )結果の図

Uniformが一様分布ね
試行回数1,000でも
あ、失敗してる
両方nの表示が2~1000になってる
修正

直したとこ
main = paste("Bernoulli, n = ", n.u[j], sep = "" ),を
main = paste("Bernoulli, n = ", n.b[j], sep = "" ),に修正(最後のhistのとこね)
はい、話がずれました。
結論

一様分布はn=10とか100でも大体それっぽくなりますね。
ベルヌーイはn=100000でやっときれいな正規分布になると言えるかなあと
コードの解説は飲み会の後で気が向いたらやります。(絶対やらんやつ)
それでは!
いいなと思ったら応援しよう!

