
スパイキングニューラルネットワークでMNIST(手書き数字を識別)
この記事は、改定&整理統合されました。新版はこちら⬇です。
これは何?
ひょんなことから、現在主流の人工ニューラルネットワーク(ANN)とは別にスパイキングニューラルネットワーク(SNN)なるものが存在することに気付きました。ANNについてはすでにニューロン版と行列版を実装したのでSNNの実装もこの調子で…と思ったのですがあまりにも違いすぎます!
ANNは連鎖律がベースですが、SNNは神経回路シミュレーションがベースになっています。神経回路シミュレーションには興味が湧いたものの、挫折せずに楽しむための足場が欲しいと思いました。そこでまずは神経回路シミュレーションの詳細には踏み込まないで、最初のゴールを「SNNで手書き数字の識別を体験する」に設定しました。
何をやったのか?
SNNフレームワークの1つ、BindsNETを使用して手書き数字の識別を実装しました。フレームワークを使っての実装なので、神経回路シミュレーションはフレームワークの中に閉じています。そのお陰で理解するのが大変な細部に囚われずに全体像を眺めることができました。また、BindsNETにはすでに有益なMNISTの識別サンプルがあったので全面的に参考にしました。
フレームワークを使うだけでは十分に焦点を絞り切れません。積極的に取り入れる部分と切り捨てる部分を考えておきます。
実装するネットワークのモデルは1つだけ選定します。
モデルの性能評価には正解率だけを使います。
ネットワークの多層化については考えません。
手書き数字の識別についてだけ考えます。
手書き数字のデータセットは2種類に対応しました。1つはMNIST(28 x 28 pix)でもう1つはdigits(8 x 8 pix)です。これらのデータセットの取得方法ですが、MNISTはtorchvisionから、そしてdigitsはscikit-learnからそれぞれ取得しました。digitsはサイズが小さいのでテスト時間を節約できます。
実装に使用したプログラミング言語はPython 3で、実行環境はGoogle Colabです。すべてのソースコードをAppendixに収録しますが、GitHubにはGoogle Colabで開けるファイルを置いておきます。
本稿には、BindsNETを使った実装を通じて分かったことを書いています。表面的な理解での記述が中心になりますが、最初の一歩としては悪くないと思います。
図解
SNNに手書き数字のトレーニングセットを投入してからマップが完成するまでの流れは次のようになります。ここで汎化されたマップを作成できれば、テストセットを投入した場合でも高い精度で手書き数字を識別できる筈です。

この図の諸条件は次の通りです。
トレーニングセット:手書き数字、1枚あたり 64 pix(8 x 8 pix)
エンコーディング: ポアソンエンコーディング
シミュレーションステップ数: 250ステップ
興奮性ニューロン1個あたりのシナプスの数: 64個(+ 抑制性 100個)
興奮性ニューロンの数: 100個
抑制性ニューロンの数: 100個
0. ネットワークのモデル
ネットワークのモデルには「Diehl&Cook(2015)モデル」を選定しました。このモデルの主要な特徴を整理しておきます。
0.1 STDP則
スパイクタイミング依存可塑性(Spike-timing-dependent plasticity, STDP)はシナプスの結合強度を調整するためのルールで次の通りです。
前ニューロンが後ニューロンよりも先行して発火した場合はシナプスの結合を強くします。これとは逆に後ニューロンが前ニューロンよりも先行して発火した場合はシナプスの結合を弱くします。実装の言い回しにすると、前者では重みに対してプラス(+)の更新量を適用し、後者では重みに対してマイナス(ー)の更新量を適用します。更新量については、発火の時刻差が小さいほど大きな更新量にします。なお、現実の実装ではスパイクトレースの手法により効率化を図ります。
STDP則は教師信号なしでシナプスの結合強度を調整するので、教師なし学習に含まれます。
0.2 側抑制(WTA)
Diehl&Cook(2015)モデルのネットワークは3層構造(入力層、興奮性層、抑制性層)になっています。この中で、抑制性層が側抑制(Winner-take-all, WTA)を担います。
WTAは1つの興奮性ニューロンが発火したときに、他のすべての興奮性ニューロンの発火を抑制します。このようにして興奮性ニューロンの均一化を防いで多様性を確保すると、利用価値のあるマップを作ることができます。
1. ポアソンエンコーディング
生物のニューラルネットワークは外の世界をスパイク信号に変換して取り込みますが、これはSNNでも同じです。今回は手書き数字をSNNに投入しますが、これをスパイク信号(スパイクトレイン)に変換する方法として、ポアソンエンコーディングを採用します。スパイクトレインはニューロンの発火の様子{0, 1}を時間軸に沿って並べたもので、これをシナプスに渡します。
2. シナプスのモデル
シナプスにスパイク信号が到着すると、コンダクタンス(電気伝導力)がシナプスの重みに比例して急激に上昇します。コンダクタンスが上昇するとシナプス電流も増加します。コンダクタンスは時間とともに指数関数的に減衰して行きますが、新たなスパイク信号が到着すると再び上昇します。シナプス電流は、スパイク信号の時系列情報を反映するとともにコンダクタンスによって変調された信号となってニューロンに渡されます。
Diehl&Cook(2015)モデルではシナプスのモデルとして、コンダクタンスベース(Conductance-based)モデルを採用しています。
3. ニューロンのモデル
ニューロンは複数のシナプスから信号を受け取り、これらを時間軸上で積分したものを総入力とします。ニューロンの膜電位はこの総入力に応じて変化しますが、膜電位が発火閾値を超えるとスパイク信号を出力します。その後ニューロンは一定期間の不応期に入り、その間は新たなスパイク信号を生成することができません。不応期が終了して膜電位が静止膜電位に復帰したところで、ニューロンは再び同様のプロセスを繰り返します。
Diehl&Cook(2015)モデルではニューロンのモデルとして、リーク積分発火モデル(Leaky Integrate-and-Fire Model, LIF)を採用しています。
4. マッピング
手書き数字を識別できるようにするには、ニューロンとラベル(ニューロンが反応した数字)の対応を示すマップを作成しておきます。マップの作成方法については残念ながら現在の理解レベルでは説明できませんが、思い切り簡略化すると次のようになると思います。モデルの訓練において例をあげると、正解値ラベル「5」が付与された手書き数字を投入したときにニューロン#45が強く反応したのなら、ニューロン#45にはラベル「5」を割り当てるといった具合です。
適切なハイパーパラメータを使って訓練すれば、利用価値のあるマップが出来上がるでしょう。マップの使い方についてはこのあとの演習で重点的に確認します。
演習
ソースコード(Appendixに収録)は後回しにして、手書き数字の識別を体験します。注意点として、ニューラルネットワークでは積極的に乱数を使うのでスクリーンショットや実行例が本稿と同じくならない可能性を指摘しておきます。本稿と同じ結果を得られることを期待して乱数シードを固定していますが、どうなるかは分かりません。
1. データセットの属性
データセットの属性はMNISTとdigitsのそれぞれで定義します。データセットの属性はデータセットの根本的な特徴を表していますが、サブセット(トレーニングセット、テストセット)のサイズについては最大数を超えない範囲で変更しても構いません。
class DA_mnist: # Dataset Attributes for MNIST
n_train = 300 # トレーニングセットのデータ件数(最大:60,000件)
n_test = 50 # テストセットのデータ件数(最大:10,000件)
inputs = 784 # 入力数(28x28)
shape = (1, 28, 28) #
classes = 10 # 10種類(0-9)に分類できる
class DA_digits: # Dataset Attributes for digits
n_train = 300 # トレーニングセットのデータ件数(最大:1,347件)
n_test = 50 # テストセットのデータ件数(最大:450件)
inputs = 64 # 入力数(8x8)
shape = (1, 8, 8) #
classes = 10 # 10種類(0-9)に分類できる2. ハイパーパラメータ
ハイパーパラメータはモデルの精度に大きく影響します。SNN(神経回路シミュレーションとBindsNET)に対する理解が深まれば適切なチューニングが可能になると思いますが、ANNの知識でいじれるのはエポック数とニューロン数ぐらいです。
class HP: # Hyperparameter
seed = 3407 # 乱数シード
exc = 22.5 # シナプスの強度(興奮性層→抑制性層)
inh = 120 # シナプスの強度(抑制性層→興奮性層)
time = 250 # シミュレーション時間
dt = 1.0 # 時間分解能
nt = int(time / dt) # シミュレーションステップ数
neurons = 100 # ニューロンの数
epochs = 10 # エポック数
n_trace = 5 # マップを更新する前のトレース回数3. 想定正解率(コードの自己診断で使用)
コードが確実に動いていると確信できる状態になったら、訓練ステップごとの正解率を収集しておきます。これを想定正解率として保存しておくと、コードの自己診断に利用できます。これは、演習ではほとんど意味がありませんが実装作業中は必須です。
assumed_accu_mnist = [ 0.00, 10.00, 26.67, 30.00, 28.00, 23.33, 25.71, 25.00, 24.44, 24.00 ]
assumed_accu_digits = [ 0.00, 10.00, 20.00, 20.00, 32.00, 33.33, 42.86, 45.00, 48.89, 50.00 ]4. データセットの読み込み
今回の演習で使うデータセットのデフォルトはdigitsにしてあります。データの視覚化に関心がなければMNISTに変更しても構いませんが、このあとのデータの視覚化で表示が細かくなりすぎて手に負えなくなるでしょう。
set_seed(HP.seed) # 乱数シードをリセット
vis = Visualizer # Visualizerの短縮名をvisとする
'''
assumed_accu = assumed_accu_mnist # MNISTの想定正解率をセット
DA = DA_mnist # MNISTの属性をセット
DS = DatasetMNIST() # MNISTデータセットを選択
'''
assumed_accu = assumed_accu_digits # digitsの想定正解率をセット
DA = DA_digits # digitsの属性をセット
DS = DatasetDigits() # digitsデータセットを選択
DS.load(HP, DA) # データセットの読み込み5. 手書き数字を表示
モデルの訓練を始める前に、ネットワークに投入するデータがどのようなものかを確認しておきます。トレーニングセットから10枚の画像を選択してイメージを表示します。選択範囲は画像#10から画像#19までです(数字の5が含まれている範囲を選びました)。画像は荒いですが、細かすぎるとデータの意味を理解するのが困難になるのでこれくらいが丁度良いです。
vis.show_dataimage(DS.ss_train.data[10:20], DS.ss_train.label[10:20])
6. スパイクトレインの生データを表示
ここからは上図の右下端にある画像#19(Label=5)のスパイクトレイン#19を見ていきます。なお、スパイクトレインの生データは時間軸(シミュレーションステップ)が縦軸になっていてグラフ化したときに不自然なので、転置の操作を加えて横軸に移動しています。
sample = DS.ss_train.spiket[19].view(HP.nt, DA.inputs).Tこのスパイクトレイン#19は画像#19(256階調)をポアソンエンコーディングした結果です。まずは、スパイクトレイン#19のデータの実態を知るために生データを表示するところから始めます。
pd.DataFrame(sample)
7. ラスタープロットを表示
生データからはスパイクトレインの実態が{0, 1}であることを確認できますが、全体像を把握できません。そこでスパイクイベント(データが1の部分)だけを点灯させたラスタープロットを表示してみます。
vis.show_rasterplot(sample)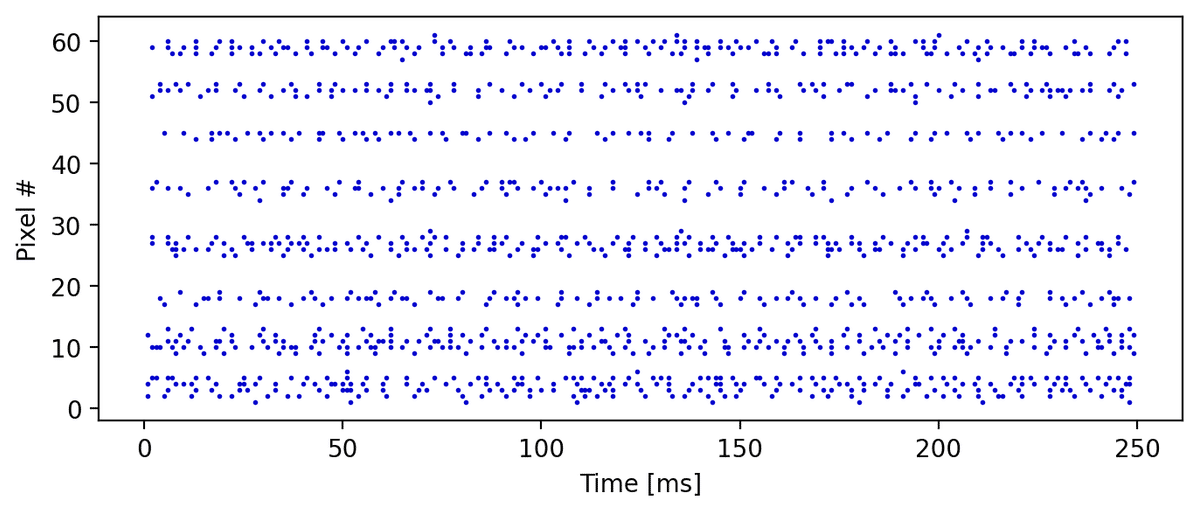
8. スパイクトレインを表示
折角なので、最初の8画素分についてスパイクトレインの一般的なイメージを表示してみます。ただし、8本のスパイクトレインを1枚の画像に詰め込むので見易さを取ってベースラインの描画を省略しました。トレーニングセットの画像#19(Label=5)において、画素#0と画素#7はそれぞれ画像の左端と右端に位置して階調データが0なのでスパイクイベントがありません。
vis.show_spiketrain(sample[0:8])
9. モデルを訓練
ネットワークにトレーニングセットを投入してモデルを訓練します。デフォルトではコードを診断しませんが、コードを診断するように変更しても構いません。
model = Model(HP, DA)
'''
model.fit(DS.ss_train, HP.epochs, HP.n_trace, assumed_accu) # コードの自己診断を行う
'''
model.fit(DS.ss_train, HP.epochs, HP.n_trace) # コードの自己診断を行わない
epoch = 1 / 10, update = 5 / 300, accuracy = 0.00%, time = 1.5秒(0分)
epoch = 1 / 10, update = 10 / 300, accuracy = 10.00%, time = 3.6秒(0分)
epoch = 1 / 10, update = 15 / 300, accuracy = 20.00%, time = 6.3秒(0分)
epoch = 1 / 10, update = 20 / 300, accuracy = 20.00%, time = 9.3秒(0分)
epoch = 1 / 10, update = 25 / 300, accuracy = 32.00%, time = 14.3秒(0分)
epoch = 1 / 10, update = 30 / 300, accuracy = 33.33%, time = 17.3秒(0分)
epoch = 1 / 10, update = 35 / 300, accuracy = 42.86%, time = 19.3秒(0分)
epoch = 1 / 10, update = 40 / 300, accuracy = 45.00%, time = 20.4秒(0分)
epoch = 1 / 10, update = 45 / 300, accuracy = 48.89%, time = 21.6秒(0分)
epoch = 1 / 10, update = 50 / 300, accuracy = 50.00%, time = 22.9秒(0分)
(・・・ 途中省略 ・・・)
epoch = 10 / 10, update = 255 / 300, accuracy = 87.06%, time = 772.9秒(13分)
epoch = 10 / 10, update = 260 / 300, accuracy = 87.31%, time = 774.7秒(13分)
epoch = 10 / 10, update = 265 / 300, accuracy = 87.55%, time = 776.7秒(13分)
epoch = 10 / 10, update = 270 / 300, accuracy = 87.78%, time = 778.2秒(13分)
epoch = 10 / 10, update = 275 / 300, accuracy = 88.00%, time = 779.4秒(13分)
epoch = 10 / 10, update = 280 / 300, accuracy = 87.86%, time = 780.5秒(13分)
epoch = 10 / 10, update = 285 / 300, accuracy = 88.07%, time = 781.6秒(13分)
epoch = 10 / 10, update = 290 / 300, accuracy = 87.59%, time = 782.9秒(13分)
epoch = 10 / 10, update = 295 / 300, accuracy = 87.80%, time = 784.3秒(13分)
epoch = 10 / 10, update = 300 / 300, accuracy = 88.00%, time = 785.7秒(13分)
正解率 = 88.00%正解率は88.00%で、まずまずの成績です(MNISTでは80.67%でした)。残念なのは、訓練が終了するまでに13分かかっていて非常に遅いです。対応策は別途考えることにして先に進みます。
10. マップを表示
モデルを訓練して得られる最大の成果物はマップです。マップは、100個の興奮性ニューロンとラベル(ニューロンが反応した数字)の対応表です。この実物がどのようなものかを見ておきます。
pd.DataFrame(model.map.view(10,10))
このマップを読み取ると次のようになります。ニューロン#21は数字の3に、ニューロン#54は数字の8に、ニューロン#87は数字の6に反応します。
このマップが汎化していればテストセットを使ってモデルの性能を検証したときに高い精度が期待できます。演習の最後に、このマップとテストセットに対するニューロンの反応を照合してマップに対する理解を確実にします。
11. ラベルの出現頻度を表示
マップを見ると数字の0に反応するニューロンが多いように感じます。実際のところどうなのかラベルの出現頻度を集計してみます。
vis.show_labelcount(model.map)
マップの中で最も多いのはLabel=0で19個、逆に最も少ないのはLabel=1で6個です。このようにラベルの出現頻度は均等でないことが分かりました。これについては想像の域を出ませんが、手書き数字の1は他の数字よりも識別しやすいのではないか?そのため少ないニューロン数で対応できているのではないか?などということを考えました。
12. モデルの性能を評価
ネットワークにテストセットを投入して、訓練済みのモデルがどれくらいの性能(識別精度)を発揮するのか確かめます。
set_seed(HP.seed)
model.eval(DS.ss_test)data = 0, pred = 7, label = 7, judge = ✓ PASS
data = 1, pred = 1, label = 1, judge = ✓ PASS
data = 2, pred = 4, label = 4, judge = ✓ PASS
data = 3, pred = 2, label = 2, judge = ✓ PASS
data = 4, pred = 3, label = 3, judge = ✓ PASS
data = 5, pred = 4, label = 4, judge = ✓ PASS
data = 6, pred = 1, label = 1, judge = ✓ PASS
data = 7, pred = 1, label = 1, judge = ✓ PASS
data = 8, pred = 8, label = 1, judge = ✗ FAIL
data = 9, pred = 6, label = 6, judge = ✓ PASS
(・・・ 途中省略 ・・・)
data = 40, pred = 0, label = 0, judge = ✓ PASS
data = 41, pred = 3, label = 3, judge = ✓ PASS
data = 42, pred = 5, label = 5, judge = ✓ PASS
data = 43, pred = 7, label = 7, judge = ✓ PASS
data = 44, pred = 7, label = 7, judge = ✓ PASS
data = 45, pred = 6, label = 6, judge = ✓ PASS
data = 46, pred = 2, label = 2, judge = ✓ PASS
data = 47, pred = 6, label = 6, judge = ✓ PASS
data = 48, pred = 4, label = 4, judge = ✓ PASS
data = 49, pred = 8, label = 4, judge = ✗ FAIL
正解率 = 76.00%正解率は76%で、それほど良い性能では有りません(MNISTでは80%でした)。今はチューニングに興味が無いのでこのままにしておきますが、性能を改善できる余地は残っています。訓練で使用するハイパーパラメータにエポック数が有りますが、これを10から50に増やすとか、訓練で投入するデータ数を300件から1,200件に増やすとかすれば性能が向上するかも知れません。もちろん、逆に性能が劣化することもあるでしょう。
13. マップの使い方
マップを使って手書き数字を識別するには、次の3つの情報を使ってラベルごとに識別レートを計算します。その結果から、最も識別レートの高いラベルを予測値として採用します。
① マップ
② ニューロンの反応(ポイント)
③ ラベルの出現頻度
具体的な計算方法については下手な説明よりも次のコードを見た方が早いです。簡単な計算なので、① ② ③ の3つの情報があれば手作業でも計算できます。
def show_labelrate(map, rec): # ラベルの識別レートを表示
map = map.numpy() # マップ
rec = rec.numpy() # ニューロンの反応(ポイント)
print('\nラベルの識別レート:')
for label in range(10):
point = np.sum(rec[map == label]) # labelの獲得ポイントを集計
count = np.sum(map == label) # labelの出現頻度をカウント
rate = point / count # labelの識別レートを計算
if rate > 0:
print(f'label = {label}, point = {point}, '
f'count = {count}, rate = {rate:.2f}')それでは、モデルの評価結果から正解例と不正解例を1つずつ選んで、これらの画像(スパイクトレイン)を手作業で投入します。そして、それぞれの画像に対して100個のニューロンがどのように反応するのか観察します。反応があったニューロンにはマーキング(赤丸)します。最後にラベルの識別レートを計算します。
【正解例】
#【正解例】 data = 47, pred = 6, label = 6, result = ✓ PASS
model.forward(DS.ss_test.spiket[47], 0) # 画像#47のスパイクトレインを投入
model.reset_state_variables()
rec = model.spike_record.sum(1)[0]
display(pd.DataFrame(rec.view(10,10))) # ニューロンの反応を表示
show_labelrate(model.map, rec) # ラベルの識別レートを表示
ラベルの識別レート:
label = 6, point = 8.0, count = 9, rate = 0.89画像#47(Lable=6)を投入すると4個のニューロンが反応しています。これらをマップと照合すると、Label=6は4個のニューロンから総取り合計で8.0ポイント獲得できます。もはや、ポイントも識別レートも関係なくLabel=6が単独勝利で予測値に採用されるので「正解」になります。
【不正解例】
#【不正解例】 data = 8, pred = 8, label = 1, result = ✗ FAIL
model.forward(DS.ss_test.spiket[8], 0) # 画像#8のスパイクトレインを投入
model.reset_state_variables()
rec = model.spike_record.sum(1)[0]
display(pd.DataFrame(rec.view(10,10))) # ニューロンの反応を表示
show_labelrate(model.map, rec) # ラベルの識別レートを表示
ラベルの識別レート:
label = 2, point = 5.0, count = 9, rate = 0.56
label = 8, point = 9.0, count = 8, rate = 1.12画像#8(Lable=1)を投入すると3個のニューロンが反応しています。これらをマップと照合すると、Label=2はニューロン#82から5.0ポイント、Label=8はニューロン#55と#97から合計で9.0ポイント獲得できます。候補が2つに分かれましたが、より識別レートの高いLabel=8が予測値に採用されて「不正解」になります。もちろん、次点のLabel=2も不正解です。
おわりに
本稿ではSNNのDiehl&Cook(2015)モデルについて全体像を把握するとともに、手書き数字の識別を体験しました。しかし、神経回路シミュレーションに踏み込めていないので、まだ何も分かっていないという確かな感覚もあります。
ひょんなことから
SNNの存在に気付いたきっかけは、Winnyの開発者である金子勇氏の誤差拡散法について調べていたときのことです。金子氏のニューラルネットワークは神経回路シミュレーション系と言っても良さそうです。これ自体も興味深いのですが、あとあと神経回路シミュレーションからしっかり取り組もうと思ったら参考資料が豊富な方が良いだろうということで、金子勇氏の誤差拡散法ではなくSNNを軸にして進むことにしました。
駆り立てるもの
AIは人類史においても記念碑的な意味があると思いますが、それを支えるニューラルネットワークの発展をリアルタイムで楽しめる機会に恵まれて幸運だと思っています。何しろ、こんな時代が訪れるのは数十年は先の話だと思ってたので。これからも優れた研究者や書き手が現れて、驚きと楽しみを共有してくれることを願ってます。
実行速度が遅い問題について
実行速度が遅い問題を解決する方法としては、処理系をPython以外のものに変更することを考えています。候補としては次のものがあります。
・Mojo(Pythonのスーパーセット、処理速度が速い)
・Julia(科学技術計算、機械学習などに適している)
今のところ、GPUの積極的な活用については考えていません。
Appendix
ソースコード
BindsNETのインストール
!pip install git+https://github.com/BindsNET/bindsnet.gitBindsNETのインストールには3〜4分くらいかかります。ローカル環境だと1度だけインストールすれば良いのですが、Google ColabではNotebookを開くたびにインストールする必要があります。
インポート/ユーティリティ/環境設定
#-------------------------------------------------
# インポート
#-------------------------------------------------
from abc import ABCMeta, abstractmethod
from types import SimpleNamespace
from time import time as t
import random
import sys
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
from bindsnet.models import DiehlAndCook2015 # Diehl&Cook(2015)モデル
from bindsnet.encoding import PoissonEncoder # ポアソンエンコーダ
from bindsnet.evaluation import all_activity, assign_labels
from bindsnet.network.monitors import Monitor
from torchvision.datasets import MNIST # 手書き数字(MNIST)
from sklearn.datasets import load_digits # 手書き数字(digits)
from sklearn.model_selection import train_test_split
import sklearn.preprocessing as preproc
#-------------------------------------------------
# ユーティリティ
#-------------------------------------------------
def set_seed(seed): # 乱数シードを設定
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
#-------------------------------------------------
# 環境設定
#-------------------------------------------------
%config InlineBackend.figure_format = 'retina' # 高精細で図を描画する
np.set_printoptions(formatter={'float':'{: .8f}'.format}) # 数値の表示を整えるデータセット
class DatasetBase(metaclass=ABCMeta):
def __init__(self):
self.ss_train = None # トレーニングセット
self.ss_valid = None # バリデーションセット(今回は見送り)
self.ss_test = None # テストセット
@staticmethod
def shuffle(data, label): # 要素の対応関係を保ったままシャッフル
zipped = list(zip(data, label))
np.random.shuffle(zipped)
return zip(*zipped)
@staticmethod
def restruct(ds, shape): # データセットを共通化するための再構築
def convert(data): # とりあえず、画像認識専用バージョン
data = torch.tensor(data/16*255, dtype=torch.uint8) # 17階調から256階調に変換
data = data.view(-1, shape[1], shape[2])
return data
ss_train = SimpleNamespace()
ss_test = SimpleNamespace()
ss_train.data, ss_test.data, ss_train.targets, ss_test.targets \
= train_test_split(ds.data, ds.target, test_size=0.25, shuffle=False)
ss_train.data = convert(ss_train.data)
ss_test.data = convert(ss_test.data)
return (ss_train, ss_test)
@staticmethod
def preproc(HP, org, size, shape): # シャッフル、スライス、エンコード
ss = SimpleNamespace()
(ss.data, ss.label) = DatasetBase.shuffle(org.data, org.targets)
ss.data = torch.tensor(np.array(ss.data[:size]))
ss.label = torch.tensor(np.array(ss.label[:size]))
encoder = PoissonEncoder(time=HP.time, dt=HP.dt)
ss.spiket = torch.tensor(
np.array([ encoder(data) for data in ss.data ]) # ポアソンエンコーディング
).view(size, HP.nt, shape[0], shape[1], shape[2]) # 配列の形状をBindsNETに合わせる
return ss
@abstractmethod
def load(self, HP, DA): # データセットの読み込みと前処理
pass
class DatasetMNIST(DatasetBase): # MNISTデータセット
def load(self, HP, DA):
ss_train = MNIST(root='./data', train=True, download=True)
ss_test = MNIST(root='./data', train=False, download=True)
self.ss_train = self.preproc(HP, ss_train, DA.n_train, DA.shape)
self.ss_test = self.preproc(HP, ss_test, DA.n_test, DA.shape)
class DatasetDigits(DatasetBase): # digitsデータセット
def load(self, HP, DA):
digits = load_digits() # データ数 = 1,797件
(ss_train, ss_test) = self.restruct(digits, DA.shape)
self.ss_train = self.preproc(HP, ss_train, DA.n_train, DA.shape)
self.ss_test = self.preproc(HP, ss_test, DA.n_test, DA.shape)データセットから2つのサブセット(トレーニングセットとテストセット)を作ります。バリデーションセットは作りません(今回は見送り)。それぞれのサブセットには3つのプロパティ(data, label, spiket)があり、spiketにはdataをポアソンエンコーディングした結果(スパイクトレイン)が入っています。また、labelにはdataに描かれている手書き数字の正解値が入っています。
ビジュアライザ
class Visualizer:
@staticmethod
def show_dataimage(data, label, fs=(6,4)): # データを256階調グレー画像として表示
plt.figure(figsize=fs)
plt.subplots_adjust(wspace=0, hspace=0)
for (i, (data, label)) in enumerate(zip(data, label)):
plt.subplot(2, 5, i + 1)
plt.axis('off')
plt.title(int(label))
plt.imshow(data, vmin=0, vmax=255, cmap='Greys')
plt.show()
@staticmethod
def show_rasterplot(spiket, fs=(8,3)): # ラスタープロットを表示
plt.figure(figsize=fs)
x_axis = range(spiket.shape[1])
raster = np.where(spiket == 0, np.nan, spiket) # 0をNaNに置換
for (i, raster) in enumerate(raster):
plt.scatter(x_axis, raster*i, s=1.0, c='mediumblue')
plt.xlabel('Time [ms]')
plt.ylabel('Pixel #')
plt.show()
@staticmethod
def show_spiketrain(spiket, fs=(8,4)): # スパイクトレインを表示
plt.figure(figsize=fs)
plt.grid(True, linestyle='--', linewidth=0.5)
event = [np.where(_)[0] for _ in spiket] # スパイクイベントを収集
plt.eventplot(event, linelengths=0.5, colors='mediumblue')
plt.xlabel('Time [ms]')
plt.ylabel('Pixel #')
plt.show()
@staticmethod
def show_labelcount(map, fs=(5,4)): # ラベルの出現頻度を表示
plt.figure(figsize=fs)
label, counts = np.unique(map, return_counts=True)
plt.bar(label, counts, align='center')
for (i, count) in enumerate(counts):
plt.text(i, count, str(count), ha='center', va='bottom')
plt.xlabel('Label')
plt.ylabel('Count')
plt.xticks(label)
plt.show()pyplotを使った視覚的にリッチな描画機能をまとめてあります。SNNで象徴的なラスタープロットやスパイクトレインなどの描画機能が含まれています。
メトリクス
class Metrics:
def __init__(self, epochs=None, n_train=None):
self.epochs = epochs
self.n_train = n_train
self.reset()
def reset(self, epoch=None): # 正解率の算出用データを初期化
self.epoch = epoch
self.count = 0 # 正解数のカウント
self.total = 0 # データの総数
def update(self, labels, pred): # 正解率の算出用データを更新
labels = torch.tensor(labels)
self.count += torch.sum(labels == pred).item()
self.total += len(labels)
@staticmethod
def judge(flag): # 論理値を判定文字列に変換
return '✓ PASS' if flag else '✗ FAIL'
def selfdiag(self, assumed_accu): # コードの自己診断(想定正解率を利用)
actual_accu = round(self.count / self.total * 100, 2)
matched = actual_accu == assumed_accu
print(f'actual accu = {actual_accu:.2f}%, '
f'assumed accu = {assumed_accu:.2f}%, '
f'result = {self.judge(matched)}\n')
assert actual_accu == assumed_accu, \
'The code may be broken.' # 実行正解率と想定正解率が一致しなかったので中断
def show_progress(self, step, time): # 進行状況を表示
actual_accu = round(self.count / self.total * 100, 2)
print(f'epoch = {self.epoch + 1} / {self.epochs}, '
f'update = {step + 1:>3d} / {self.n_train}, '
f'accuracy = {actual_accu:.2f}%, '
f'time = {time:.1f}秒({round(time/60)}分)')
def show_judge(self, step, label, pred): # 判定結果を表示
matched = label == pred
self.count += int(matched)
self.total += 1
print(f'data = {step:>2d}, pred = {pred}, '
f'label = {label}, '
f'judge = {self.judge(matched)}')
def show_result(self): # 最終的な結果を表示
print(f'正解率 = {self.count / self.total * 100:.2f}%')モデルの性能評価に必要な指標を管理します。正解率以外の指標はバッサリ切り捨てたので、モデルの性能を評価する手段はこの正解率だけです。メトリクスには想定正解率を利用したコードの自己診断機能が含まれています。実行正解率と想定正解率が異なる場合は、開発中にコードを破壊したものと見做して例外を生成してプログラムを停止します。
ネットワーク
class Network(DiehlAndCook2015):
def __init__(self, HP, DA):
super().__init__(
n_inpt = DA.inputs, # 入力層における入力数
n_neurons = HP.neurons, # ニューロンの数(興奮性、抑制性)
exc = HP.exc, # シナプスの強度(興奮性層→抑制性層)
inh = HP.inh, # シナプスの強度(抑制性層→興奮性層)
dt = HP.dt, # 時間分解能
norm = DA.inputs / 10, # 接続強度の正規化(入力層→興奮性層)(学習に大きく影響する)
inpt_shape = DA.shape) # 入力データの形状
self.spikes = self.__set_spiketracer(HP.nt)
self.map = -torch.ones(HP.neurons)
self.rates = torch.zeros((HP.neurons, DA.classes))
self.HP = HP
self.DA = DA
def __set_spiketracer(self, nt): # スパイクトレーサーを設定
spikes = {}
for layer in set(self.layers):
spikes[layer] = Monitor(
self.layers[layer],
state_vars = ['s'],
time = nt)
self.add_monitor(spikes[layer], name='%s_spikes' % layer)
return spikes
def trainmode(self, mode, size): #
self.train(mode=mode)
self.spike_record = torch.zeros((size, self.HP.nt, self.HP.neurons))
def forward(self, spiket, index): # 入力層にスパイクトレインを投入する
s = self.DA.shape
X = { 'X': spiket.view(self.HP.nt, 1, s[0], s[1], s[2]) }
self.run(inputs=X, time=self.HP.time)
self.spike_record[index] = self.spikes['Ae'].get('s').squeeze()
def predict(self): # 予測
return all_activity(
spikes = self.spike_record,
assignments = self.map,
n_labels = self.DA.classes)
def mapping(self, labels): # マップ(ニューロンとラベルの対応表)を更新
self.map, _, self.rates = assign_labels(
spikes = self.spike_record,
labels = torch.tensor(labels),
n_labels = self.DA.classes,
rates = self.rates)ネットワークはDiehl&Cook(2015)モデルの拡張として実装しました。とは言うもののモデルの核心部分はフレームワークの中に閉じているので、かろうじてマッピングの結果を変数「map」に取り込んで良しとしました。
モデル
class Model(Network):
def __init__(self, HP, DA):
super().__init__(HP, DA)
def fit(self, ss, epochs, n_trace, assumed_accu=None): # モデルを訓練
self.trainmode(mode=True, size=n_trace)
start = t()
total = len(ss.spiket)
index = range(total)
metrics = Metrics(epochs, total)
for epoch in range(epochs):
metrics.reset(epoch)
labels = []
whole = iter(zip(ss.spiket, ss.label))
for step in range(0, total, n_trace):
for i in index[step:step+n_trace]:
(spiket, label) = next(whole)
self.forward(spiket, i % n_trace)
self.reset_state_variables()
labels.append(int(label))
pred = self.predict()[0:len(labels)]
self.mapping(labels) # n_trace回に1回、マップを更新する
metrics.update(labels, pred)
metrics.show_progress(i, t()-start)
idx = step // n_trace
if assumed_accu and epoch == 0 and idx < len(assumed_accu):
metrics.selfdiag(assumed_accu[idx])
labels = []
metrics.show_result()
def eval(self, ss): # モデルの性能を評価
self.trainmode(mode=False, size=1)
metrics = Metrics()
for step, (spiket, label) in enumerate(zip(ss.spiket, ss.label)):
self.forward(spiket, 0)
pred = self.predict()
metrics.show_judge(step, int(label), int(pred)) # 判定結果を表示
self.reset_state_variables()
metrics.show_result()モデルはネットワークの拡張として実装しました。モデルの実装まで来るとSNNの細部がかなり隠蔽されているので、ANNでの実装と大きく変わるものでは有りません。
参考資料
このサイトがなければ最初の一歩を踏み出すのが難しかったと思います。
本稿の実装で使用したBindsNETのGitHubです。実装の核心部分(APIの呼び出し部分)は eth_mnist.py に拠っています。APIのソースコードは次のファイルに有ります。
・Monitor bindsnet / network / monitors.py
・add_monitor() bindsnet / network / network.py
・run() bindsnet / network / network.py
・all_activity() bindsnet / evaluation / evaluation.py
・assign_labels() bindsnet / evaluation / evaluation.py
このページの最後までスクロールすると、『ゼロから作るSpiking Neural Networks 第2.1版』(Python)のPDFを入手できます。
本書のPDF(高校生向け抜粋)が公開されています。
本書のPDF(計算神経科学への招待)が著者によって公開されています。
更新履歴
2024-06-22、初版
2024-08-09、「ポアソン分布(Poisson distribution)」を「ポアソン過程(Poisson process)」に訂正2024-08-10、ポアソンエンコーディングに関する記述から次の文を削除『名前から想像できるように、この変換にはポアソン分布(Poisson distribution)が応用されています。』
