
類型論を学ぶ②『パーソナリティの研究と心理統計①』
この記事について(前回のコピペ)
以下、本文は口頭説明用の原稿を書き写したものです。
どれも文献の情報を参考にしていますが、表現を口語体で伝わるように直しているので厳密な表現ではありません。また、スライドの情報は最大限正確性を期していますが、本文の原稿についてはスライドほど正確でない可能性がありますし、私見も含みます。
「~~」はスライドに記載した文言をそのまま読むのを想定した目印です(どの文言に対応するかは文脈を読んで判断してください…)。
【導入】

1点目 ~~ 私はもともと、第2回で統計の話をするつもりだった。MBTIの妥当性研究を理解するには、これで間に合うと思っていた。しかし、調べていくうちに、パーソナリティの研究法や、心理学の研究法も知っておかないと、研究結果を正しく理解できないと思うようになった。どうしてもここを通らないといけない。遠回りになるが、今日は一般論からはじめる。
個人的な関心や興味で心理学を学びたい人はたくさんいる。多くの需要は、心理学は何を明らかにしてきたのかという成果の部分である。研究のやり方は研究者が知っていればいいように思えるが、そうではない。結論そのものと、その結論をどうやって導いたかという点は切っても切り離せない。
正しい知見を得るには、ただの俗説や疑似科学との見分けがつかなければならない。そのためには、論文に書かれている主張の根拠、推論のやり方、データの集め方、解釈のしかたが適切かどうかを、自分の力で検討できないといけない。でないと、ウソや噂に惑わされる。誰かがこの理論は科学的ではないと言っていたからそうなんだ、と決めつける態度も科学的ではない。最後は自分の頭で判断しないといけない。今日の目標は、その判断のための基本的なフレームを理解することにある。これをモチベーションに頑張っていこう。
あと、3点目、データの解釈でどうしても数学を避けて通れないので、今日の後半から次回にかけて話していく。
【心理学研究法】
導入

4段階のプロセス ~~
①まず、研究の目的を明らかにする。これがリサーチクエスチョン。研究の方向性は2つある。人間の行動を観察して、法則や仮説を作る帰納的なやり方と、与えられた仮説に沿ったデータが得られるかを検証する演繹的なやり方がある。それぞれ、探索型と検証型に対応している。
②テーマが決まったら、データを集める。データには2種類、~~ 探索型では質的データ、検証型では量的データが取られるケースが多いようだ。量的データの扱いはパターン化されているので、一度学べばどれも同じで分かりやすい。一方で、探索型では、質的データから研究者のインスピレーションや洞察に基づいて法則を導き出すので、方法論としてまとめにくい一面がある。
また、心理学の研究対象は基本的に人間だが、この相手とどういう関係でデータを取るかという観点から、3つのアプローチがある。
調査研究:研究者は現実に手を加えないで、ありのままの状態を把握しようとするアプローチ。
実験研究:研究者が研究のために人工的な状況を作る。被験者にはその状況に入ってもらい、条件を意図的に操作して、その効果を調べる。
実践研究:現実に介入して、対象者に働きかけるのを研究の目的としている。教育や臨床の場面でなされる。
③データを集めたら、それらの分析と解釈をする。探索型、検証型それぞれ、~~ 量的データの分析で、統計的な手法を使う。ただ、大事なのは、分析や解釈はあくまで研究者が行うものであるということ。いまは便利な統計ソフトもあるので、それを使えば自動的に解釈を導いてくれると錯覚してしまうが、そうではない。Big Five研究で用いた因子分析でも、特性の類似度は数値計算で出してくれるが、その先、ではいくつの潜在因子があるのかという解釈や、ネーミングは人間が考えて答えを出している。このことは心に留めておきたい。
質的調査

ここから、質的調査の流れを話していく。ここまでを振り返ると、質的研究、特に質的な調査研究では、仮説を作るのがゴールだった。つまり、新しい概念や法則、モデルを提案するスタイルと結びつきやすい。質的研究を行うには、たいてい質的データを集める。そして、質的データを使って、多くは質的な分析をする。では、「質的」とは何なのかを、掘り下げていこう。
「質的」とは、一言で言うと、3点目、事実の記述をいう。記述というのは、~~ 変なたとえだが、質的分析はWordで行って、量的分析はExcelで行うイメージ。では、どんな方法でデータを集めるかというと、~~
フィールドワークというのは、調べたい出来事が起きている現場に行って調査することをいう。フィールドに身を置いて、見る、聞く、触る、感じる、味わう、五感を通した生の体験に基づいた調査が醍醐味。観察や面接以上に、研究者が積極的に対象に関与している、そういう手法。
言葉で正しく分析するのは難しい(4,5点目)。データを集める時点で観察者の偏見が混じっているから、収集と分析を切り離すこともできない。同じデータを集めたとしても、解釈は人それぞれで、研究者にとって当然幅のある結論が出てしまう。⇒複数人の関与を重視

質的な分析では何をするのか、喩えを使って話してみよう。たとえば、「青と赤の色の違い」をテーマにしたとする。量的なアプローチを採ると話は簡単で、たとえば赤と青の波長を明らかにすれば違いを説明できる。しかしこれだけでは、色の違いをすべて表現できたとはいえない。心理学は人間を対象としている、とすると、たとえば色の違いに対応して、主観的な知覚体験はどう変わるのか ―気分が高まる、落ち着くなど― を表現したいこともある。そういうときに質的なアプローチで攻める。
質的な分析でやることは、右側に書いてあるとおり。~~ ここで言葉が大きな役割を果たす。言葉というのは、世界の一部を切り取って指し示す役割がある。概念も主に言葉によって表される。質的研究が目指すのは、言葉を通じて、新たな概念や、ひとまとまりのアイディア、体系を提案することにある。そこにいきつくために、記述データを集めて、解釈して、さらに分類や類型化もしていく。
パーソナリティの類型論仮説も、質的研究からはじまるものだろう。ユングのタイプ論もそうである。ユングの著作にも統計は出てこなかったはず。多くの観察から洞察を働かせて、パーソナリティの発達について類型化した。
近年は、文章データも自然言語処理によって実用的な分析ができている。Twitterの発言を、IBMのwatsonに投げれば、パーソナリティ分析ができる。(これも統計的な処理の一種。)こういう技術を使えば、質的研究も途中までは自動化できそうではないか? 新しい概念を作るのは人間だろう、でも類型化まではコンピュータで処理できるのではないか?
量的調査

続いて、量的調査の方法論をみていこう。左側に手順を一覧で示した。量的なデータは質問紙で集めるのが主流らしいので、質問紙法のプロセスとして紹介する。
まず、リサーチクエスチョンから仮説を立てる。ただ、この仮説やモデルは、因果関係が含まれていたり、複雑な関係性が含まれていたりして、そのまま数値データに置き換えて検証するのが難しい。だから、もう一段階かませて、相関仮説や処理―効果仮説といった、検証しやすい予測を立てる。こうすることで、この先の数値化プロセスがやりやすくなる。
調査研究では、~~(相関仮説)
MBTIの妥当性研究の例でいえば、おおもとの仮説やモデルが、16タイプの存在やタイプダイナミクスの理論にあたる。ただ、これをそのまま数値データに置き換えて検証することはできない。そこで、たくさんの相関仮説に置き換えて、そちらを検証をする。たとえば、「直観機能が強い人ほど、読書量が多い傾向にあるはずだ」「外向な人ほど、プライベートで他人と交流する機会が多い傾向にあるはずだ」という相関仮説を立てられる。

では次に、相関仮説をたてた後に、そこに出てくる概念を具体的な変数に置き換えて、対応付けをする。このことを、構成概念を観測変数に置き換えるという。構成概念というのは、~~ 観測変数は~~
先のMBTI研究の例でいえば、直観機能の強さ、読書量、外向性、交流の頻度を観測変数に置き換える。外向性や直観機能は質問紙から調べるだろう。読書量だったら、1年間に何冊の本を買ったかとか、交流頻度だったら1年間に何人の友達と関わったかとか、そういう観点から測定できる。

数値化するには尺度を作らないといけない。質問紙を使うなら、質問項目や得点化の方法を考案する。被験者の行動を観察して、時間や回数をカウントする場合はこの点はスルーでよい。質問紙も雑に作ってはだめで、作り方が決まっている。正しい方法に従わないと適切に測定できない。


観測変数を定めて尺度を作った、その尺度に基づいて測定したとしても、その結果が構成概念を正しく反映していなければ意味がない。そこで、尺度の信頼性や妥当性も一緒に検証しなければならない。
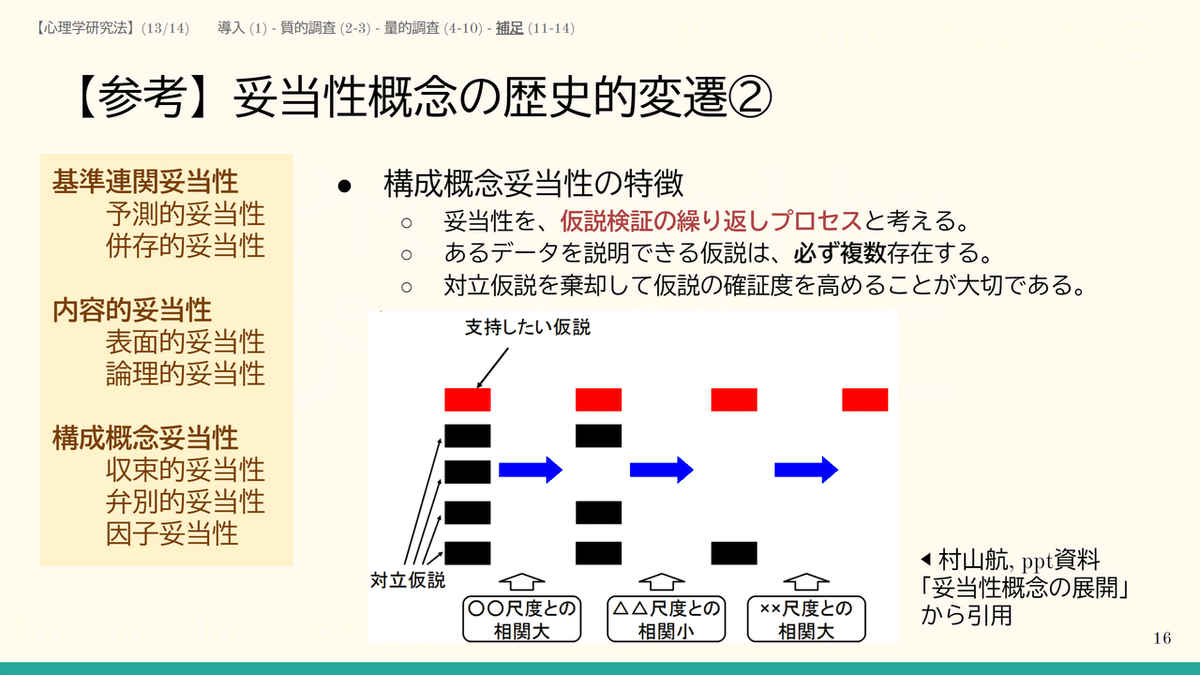
妥当性は、測りたいものを測っているかということ。妥当性の概念も多義的だが、ここでは構成概念妥当性を中心に扱う。
妥当性をたとえていうなら、その人の視力を計測したいなら視力検査表を用いなさいよ、ということ。視力を測りたいのに体重計に乗せていたら欲しいデータは手に入らない。
妥当性の検証はどうするかというと、いま着目している構成概念と似ている構成概念、もしくは理論的に似ていないはずの構成概念の測定値と比べてみる。似たもの同士は相関が高くなることを調べるのが収束的、似ていないもの同士は相関が低くなることを調べるのが弁別的。
(p.11⇒)ある視力検査表の妥当性を調べる目的で、体重データとの相関を取る方法がある。これら2変数の相関が低ければ、その視力検査表は体重を測定したものではないという弁別ができたといえる。これが弁別的妥当性。
視力と体重ほど違えば検証するまでもないが、心理学上の概念は類似しているものが多いので、弁別的証拠を十分に集めるのが大事だという指摘もある。もし収束的妥当性は得られても、弁別的妥当性が得られなかったら、その構成概念はいったい何を意味しているの? となる。別の構成概念と区別できていない、外延が不明確なもやっとした概念だということになってしまうから。
(p.10⇒)また、妥当性の前提条件として、信頼性も検証する。信頼性は、測定結果に一貫性がみられるかということ。
信頼性をたとえていうなら、身長を計測するときに、伸び縮みするゴムで測ってもそのデータは当てになりませんよ、ということ。計測するたびにブレがある尺度は使い物にならない。信頼性の検証では、数値の変わらない程度を測る。つまり何度か計測してその相関係数を取って、高い相関があれば信頼性の高いデータがとれたといえる。
信頼性の指標はたくさんある。ということは、信頼性は多義的である。どういう意味の一貫性を評価するかによって使う指標も変わる。大きく2つに分類できて、時間を超えた一貫性と項目を超えた一貫性にわけられる。時間~~ 項目はわかりにくいので補足。
(p.11⇒)構成概念はひとつの質問だけで測れるほど単純ではない。たとえば、MBTIの判断指向は、~~ これもひとつの構成概念。J 指向という構成概念を薄い黄色の円で示したとしよう。ここで「あなたは、決定することと~~」という質問をすれば1問で答えは出るが、それで分かるなら苦労はしない。そこで実際は、意味を限定して、少しずつブレを出した数十個の質問を用意する。これらの回答をすべてあわせれば、構成概念の全体を覆えるようにしておく。そうすると、ひとつの尺度を測っている項目間の相関が気になってくる。この指標を内的整合性という。内的整合性は、1つの尺度の質問群を2つに分けてその相関をとる。相関が高ければ、中の項目は似たものを測っているといえる。内的整合性の指標はいくつかあるが、α係数であれば0.80以上が望ましいとされている。1に近ければいいわけでもない。すべて同じ質問にしたらα係数は1になるが、代わりに妥当性がなくなってしまう。信頼性をあるレベルまで高めつつ、妥当性もキープできるようにするのが理想的な質問紙である。

データを取れたら次は分析と解釈に入る。後のセクションで詳しく解説。ここでは、相関関係と因果関係は違うということと、相関関係はデータで示せるが、因果関係はさらに推論を重ねなければならないものであることを押さえておきたい。

仮説やモデルは一般論。⇒多数の人々や集団に適用できるはず。その適用範囲が母集団である。しかし、母集団は、何百万人や何億人というスケールになるので、全員は調査できない。そこで実際は、母集団の中から数百人、数千人規模のサンプルを抽出して、そのサンプルに対して調査をする。
そうすると、その特定のサンプルについて得られた結論を、母集団に適用して良いのかという問題が起きる。この問題の解決のために、統計学の力を借りる。内閣支持率のアンケートと同じ問題意識。
サンプルで得られた相関係数が0.3だったとしても、母集団でも0.3といえるのか? 少なくともゼロではないと高い確証をもっていえるのか? 統計ではこのサンプルで偶然に変動する部分を取り扱う。サンプルの数がわかれば、変動の幅がどれくらいかは統計的に計算できる。この助けを借りて、サンプルの結果から母集団の結果を導く。このあたりが、次回話す検定や有意性の話。この推論過程も、ウソではないがごまかそうと思えばごまかせる。だから統計も学んでおく必要がある。
補足

一点補足。先ほど、仮説が正しいならある予測が立つ、その予測が正しければ仮説を検証できるといった。これは論理として正しいのか?
結論からいえば間違っている。逆は必ずしも成り立たない。ただ、現実的な問題として、H⇒Pが完全に満たされるわけでもない。そこで、「仮説を支持する、支持しない」という言い方をする。オール or ナッシングではなく、グラデーションの尺度のなかで、その研究がどれだけ説得力があるかをみていく。
そうすると、1つの研究だけで完全に仮説を検証できたとはいえなくなる。そこで、追試研究を行ったり、複数の研究の成果をまとめたメタ分析が求められる。これが今の研究スタイルのようである。だから、学ぶ側としても、できるだけ多くの文献や論文に触れていきたい。

妥当性の概念は歴史的に移り変わりがある。インターネットでも、古い考え方が紹介されているサイトがある。妥当性は重要な概念だが、重要なあまりいろんな人がいろんなことをいうので訳が分からなくなりがち。妥当性について混乱している方向けの資料を載せておく。
「尺度がそのまま概念を表す」というのは、学校のテストで何点取れたかがそのままその科目の学力を反映しているのだという考えに近い。学力をあえて別に定義しない。

【パーソナリティの研究法】



ポイントは、質問紙法は本人が意識できている側面を測定している点。だから、モデルの中に無意識の存在が組み込まれていると、質問紙法だけでは十分な検証はできないように思う。
また、質問紙法は何を測っているかが受検者にも見当が付く。だからいくらでも結果を操作できる。この点からも、質問紙法だけに頼った検証は危ないといえる。
【記述統計】
本論
調査を通して量的データを集めたとする。次はこれらの膨大なデータをさばかないといけない。データを正しく、効率的に読むための方法が記述統計。まずは1つの変数の扱い方をみていこう。その後、2変数に増やしていく。多変数になると、変数と変数の間の関係も表現していくので複雑になる。

ひとつの分布(データの集まり)をひとつの値で代表させる代表値と、分布の広がり具合を表す散布度がある。
代表値は、平均を知っておけばよい。観測値をすべて足してデータの個数で割る。代表値をどう定めるかというのは、べき論。代表値としての適切さを定式化して、適切さがmaxになる値を代表値とする。適切さは、数学の問題から離れているので、他の決め方もある。
これから数式が出てくるが、添え字とΣの記号に慣れておきたい。これから意味の違う変数がたくさんでてきたり、1つの変数でも何百人の観測値を扱ったりするので、ひとつずつ別の文字を割り当てていたらきりがない。そこで、xという変数について、1番目の人の観測値をx1、2番目の人の観測値をx2、…というように表す。また、Σは和を簡単に表す記号。毎回、x1+x2+x3+…と表現したら疲れるので、Σでまとめる。この場合、iを1から動かしてNまで足すということ。
それから2つめ、散布度は分散と標準偏差。分散は、それぞれの観測値と平均との差(これを偏差というが)、偏差の2乗を足し合わせてデータの個数で割ったものをいう。2乗しないで偏差をすべて足しても必ず0になるので役に立たない。平均が50点のテストがあって、全員が50点なら分散はゼロ、半分が0点で残りの半分が100点だったら分散は大きくなる。後者のほうが得点分布の広がりが大きいと解釈できる。標準偏差は、分散の正の平方根をとったものをいう。


まず、合成変数。国語の得点 x と数学の得点 y を足し合わせた新たな変数 z を考えましょうという話。この z が合成変数。この先の理論的な計算で使うので紹介する。
簡単な例で、和の平均は、平均の和になる。2科目合計の平均点は、国語の平均点と数学の平均点を足したものである。これはあたりまえ。一方で、合成変数の分散はそうはならない。国語の分散と数学の分散のほか、共分散と呼ばれる指標 s_xy を2倍したものがくっつく。共分散はあとで。
次に線形変換。これは変数の尺度と基準点を変える。0~100点の尺度を、-10~+10点に変換できる。標準化はその特別な場合で、特定の平均や標準偏差を持つように変数を変換できる。(p.25⇒)素点は、それだけだと情報としての価値は低い。平均や標準偏差といった分布を知らないと相対的な立ち位置が分からないから。標準化すれば適切な比較ができるメリットがある。

2変数の関係を扱うとき、数字に着目する前に、意味を正しくとらえないと大きな勘違いにつながってしまうので整理しておく。xとyの関係というとき、心理学では次の4つのケースがある。 ~~
①相関関係の例:MBTIの外向得点とビッグファイブの外向性得点、②共変関係の例:年齢が大きくなると、取得語彙の数も大きくなる⇒その増え方は個人ごとに違うかもしれない。相関関係とは区別する。
この先、相関関係を前提として相関係数や回帰直線に話を進める。

では、データの処理をみていこう。2変数の相関をみるとき、まず散布図を作る。相関係数や回帰直線は、直線的な関係しか表現できない。生のデータに本当に直線関係があるといえるかを確認する。

散布図をみて直線的な関係があるなら、その向きと大きさを数値で表す。
相関係数に先だって、共分散を定義する。x,yの組のデータがたくさんある。それぞれについて、xの平均との差、yの平均との差の積をすべて足す。最後にデータの個数で割る。共分散で大事なのは符号。~~象限
次に、共分散の値が取り得る範囲を考える。x,yが最も強い関係にあるとき、つまり直線関係にあるとき、共分散の絶対値は最大になる。これは x を y に線形変換したときと同じ。このとき、共分散は、xの標準偏差とyの標準偏差の積になる。すると、共分散の値域は、~~
ところで共分散の値は、データの尺度によって変わる。テストが10点満点か100点満点かでスケールが変わってしまう。そこで、共分散を標準偏差の積で割った値を相関係数と定義する。すると、相関係数の取り得る範囲は、-1~1に揃えられる。この指標を基準にして2変数の相関関係を論じていく。

もうひとつ、2変数の分析には回帰分析の手法がある。これは、xの値が変わるとyがどれだけ変わるか、という視点から関係性を表現したもの。回帰分析には方向性がある。xからyを予測するか、yからxを予測するかで2つの答えが出る。相関係数はそういうことはなく、xとyの相関といったら1つの値しか出てこない。
回帰分析の回帰とは、いったい何への回帰か? だが、「平均への回帰」を意味している。
(⇒右下図)相関係数が小さいと、yの予測は平均に安定していく。極端な場合、相関がないということは、yを予測する上でxの情報がなにも役に立たないということ。xに関係なく、yの予測は一定値すなわち平均になる。
もっとも基本的な回帰分析では、yをxの一次式で表せると仮定する。結論から示すと、~~ 相関係数r=0だと係数b=0になるのも確かめられる。

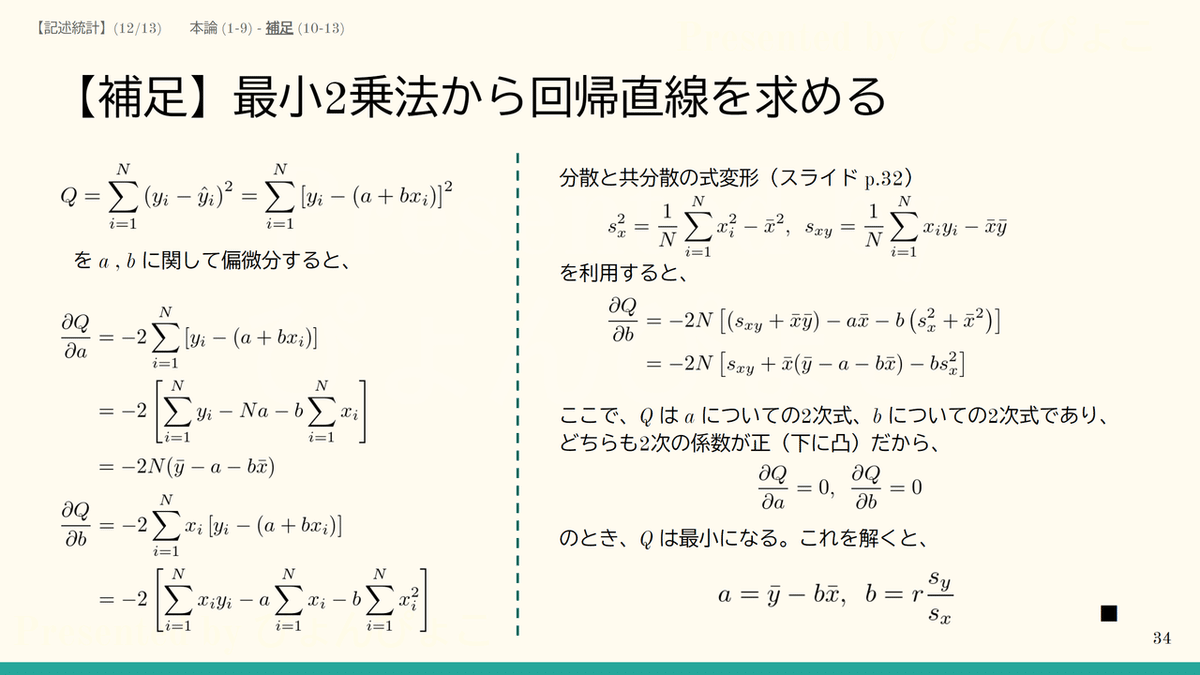
yの予測値をどうやって導くかだが、最小二乗法を使う。最小2乗基準をまず作り、この値が最小になるa,bを求める。最小2乗基準では、観測値と予測値の差をとって2乗したものの和をとる。a,b は微分を使って数学的に解ける。補足にまとめておいた。
回帰分析の重要なポイントは、yを、xに完全に相関する部分とxとは無相関の部分に分解できるということ。Qを最小にするようにa,bを定めると必ずこうなる。2点目、3点目とQが最小という仮定から導ける。これとは異なるa,bを定めて別の回帰直線も作れるが、そうすると無相関の部分だけを取り出せない。ここで、yの予測値をy^、実際の値と予測値のズレをeとすると、y=y^+eとなる。このとき、xとeの相関がゼロになるし、y^はxを線形変換したものだから、y^とeも無相関となる。このように、ある変数を無相関な2つの成分に分解することを直交分解という。直交分解で何がうれしいかを次に解説する。

メリットはずばり、yの分散を2つに分けられる点にある。合成変数の分散を先に求めたが、合成する2変数が無相関だと共分散がゼロになるので、分散の和だけで表せる。
予測値の分散と残差の分散を、yの分散と相関係数で書き換えできる。すると、yの分散(散らばり具合)について、xで説明できる散らばりと、説明できない散らばりに分けることができる。その比が、相関係数rを使って、r^2 : 1-r^2 ~~
この考え方を応用すると、人々の行動の違い、これは従属変数yの分散として表現されるが、これをたとえば、MBTIの思考と感情機能の違いによって説明できる部分と説明できない部分に分割できる。説明できる部分が大きいほど、その行動の違いは心理機能の違いと結びついていると主張しやすくなる。そうするとモデルどおりの心理機能が現にあるポジティブな証拠とできる。
補足



【引用文献】

次回、心理統計②:推定・検定、重回帰分析、分散分析、因子分析を取り扱う予定。
