
M-1の審査方法を統計学でみる
記念すべき第20回を迎えた今年のM-1グランプリですが、統計学と機械学習を最近学び始めた私には、いくつか違和感を覚える部分がありました。
それは、
審査員ごとに平均点と標準偏差を揃えなくて良いのか?
についてです。
審査員ごとに1点の重みが違った場合、全員のスコアを単に合計して順位を出すことに違和感を覚えます。
わかりやすい例を出すとすると、あそこに平均点50点の審査員がいた場合、どうなるでしょうか。
平均90点、レンジ86~94点の人がつける91点と、平均50点、レンジ10~90点の人がつける60点は同じ意味を持つでしょう。(もちろんこれは大雑把で極端な例です。)
審査員のスコアが単に合計された場合、同じ評価なはずなのに、どちらの審査員に刺さるかで9点もの差が生じてしまいます。
これは公平であると言えるでしょうか。(こんなこと言い出したらキリがないという意見はごもっともです。)
そこで、今回、私は審査員ごとに一点の重みを揃えるため、「正規化」という操作をM-1のスコアにしてみました。
正規化とは、スコア分布を平均を0、標準偏差(データのばらつき具合)を1にすることです。(詳しくはここではのべません。)
この処理により、審査員ごとに平均点と標準偏差が統一されます。
この処理を加えたことによる結果の変動を以下に示します。



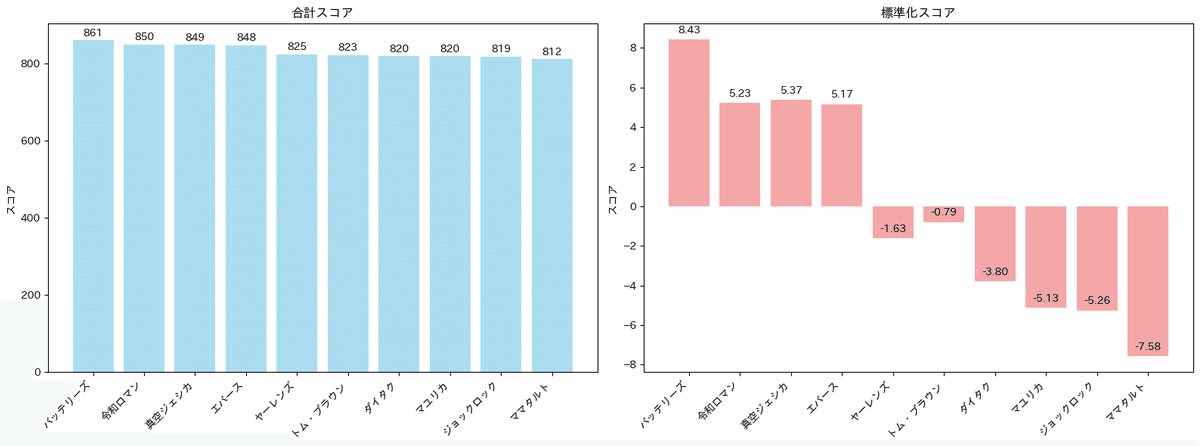
以上の結果より、スコアを正規化させた場合、順位に変動が生じることがわかりました。(外れ値の処理などは今回完全に無視しています)
ファイナルに上位3チームしかいけないことを踏まえると、正規化をするのかしないのかで、結果が変わってしまうことがあり得ることが考察として言えます。
私の好きな「エバース」がファイナルにいけたのではと思って色々分析してみましたが、4位のままでした、、、、、
今回、用いたコードは以下にあります。
