
Scratchで学ぶ!ポリオミノ・パターンの世界~P.T.P.S.チュートリアル編 その2
私がScratchで最近作ったアプリP.T.P.S (Polyomino Tiling Pattern Simulator)をチュートリアルで解説する第二回です。ここからは実際にアプリを使って説明していきます。
アプリへのリンク(Scratch):
P.T.P.S (Polyomino Tiling Pattern Simulator)
アプリスタート
まず画面拡大ボタンを押して画面を拡大モードにしてください。
次に、緑色の旗を押してアプリをスタートさせます。アプリの途中で最初からはじめたいと思ったときは、この緑の旗を押すことでいつでもアプリをリスタートできます。(ちなみに赤色の$${8}$$角形を押すといつでもアプリを停止させることができます。)

するとアプリのタイトルが表示されたスタート画面が表示されるので、この画面について少し説明します。

まず画面中央下に見えるのが、スタートボタンです。このボタンを押すと次のセッティング画面に移ります。
そして右下に見えるのがアプリ内チュートリアルの表示、非表示を切り替えることができるチェックボックスです。今回は使いませんが、右下のチェックボックスをオンにすると、
ScratchでおなじみのCatというキャラクターがでてきて、アプリの操作について一言アドバイス(英語)をしてくれるようになっています。
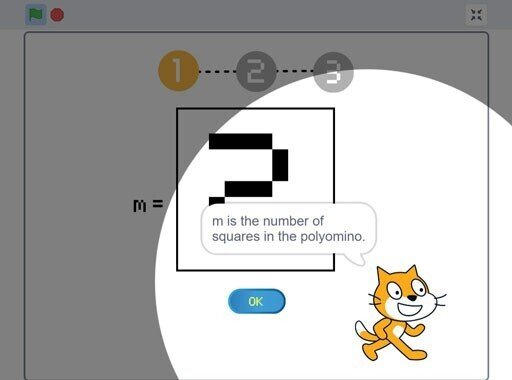
では、チェックボックスをオフにしたままスタートボタンを押します。
セッティング画面
セッティング画面その$${1}$$が現れます。この画面では、ユーザが$${m}$$の値を決めることができます。この$${m}$$というのは、ポリオミノを構成する正方形の数で、$${2}$$から$${10}$$までの好きな数を選ぶことができます。

操作としては、画面中央の枠で囲まれた大きな数をクリックすることで数が切り替わります。では、例えばここでは$${m = 5}$$とします。

数を切り替えて$${5}$$にしてから、下にあるOKボタンを押すと、セッティング画面その$${2}$$が表示されます。
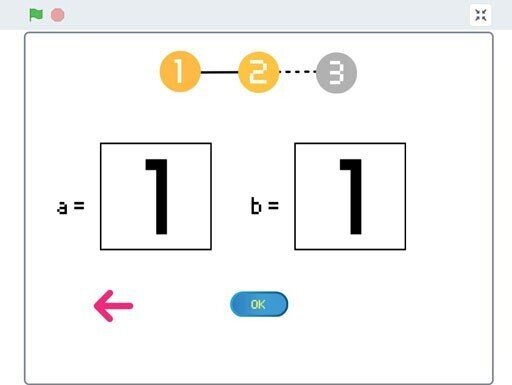
この画面では、$${a}$$と$${b}$$という二つの数を設定することができます。$${a}$$と$${b}$$はともに$${0}$$から$${m - 1}$$までの整数で、この数によりキャンバス(後述)の各セルに書かれる数字(この数字のことをセル番号と呼びます。)が変わってきます。しかしここでは余り深く考えず、例えば$${a = 2, b = 3}$$とでもしておきます。UIは先程と同様に枠で囲まれた数字をクリックすることで数が順番に切り替わるしくみです。
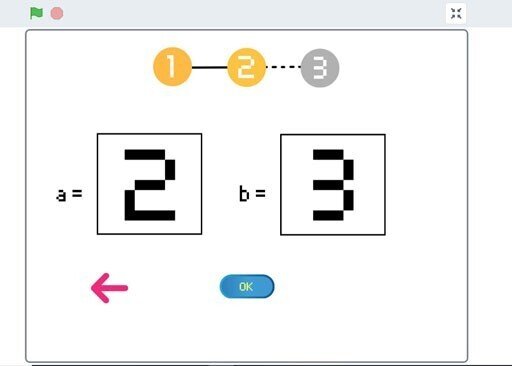
これでよかったら画面中央下のOKボタンを押します。(画面中央左にある左向きの赤い矢印を押すと、セッティング画面その$${1}$$に戻ります。)
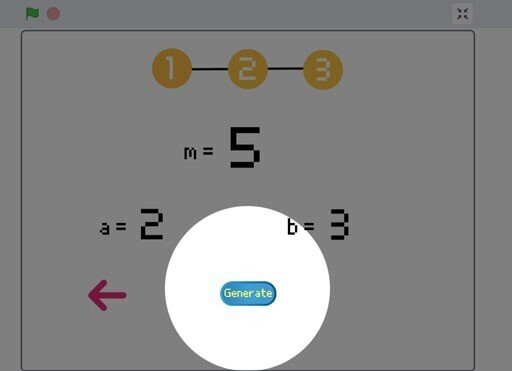
するとセッティング画面その$${3}$$が表示されます。この画面ではユーザが設定した$${3}$$つの値($${m,a,b}$$)を念押しとして表示しているので、

それでよかったら画面中央下の生成(Generate)ボタンを押します。(左向きの赤い矢印を押すとセッティング画面その$${2}$$に戻ります。)
すると少しのローディングの後で、
キャンバスと呼ばれる$${m^2}$$に並んだ正方形が現れます。この各正方形のことはセルと呼びます。
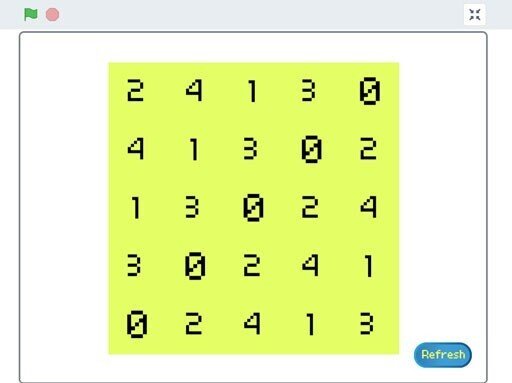
私たちは$${m = 5}$$としたので、このようにキャンバスには$${ 5^2 }$$のセルが並んでいます。各セルに注目すると、数字が表示されているのが分かると思います。この数字は各セルのセル番号といって、$${0}$$から$${m - 1}$$までの整数値をとります。では、参考までにその計算式について述べておきます。(ここは読み飛ばしてもらってかまいません。)
セル番号の計算式
キャンバスには$${m^2}$$のセルが並んでいますが、各セルには座標が決まっています。この座標というのはユーザからは見えなくてアプリで内部的に決まっている数値なのですが、次のようになります。
座標は$${0}$$から$${m - 1}$$までの整数の順序対$${ ( x , y ) }$$で表される。
一番左、一番下にあるセルの座標は$${ ( 0 , 0 ) }$$で、この座標のことを原点と呼ぶ。
原点から$${x}$$右、$${y}$$上にあるセルの座標は$${ ( x , y ) }$$。
例えば、原点から$${2}$$右、$${4}$$上にあるセルの座標は$${ ( 2 , 4 ) }$$で表されます。このようにして、各セルの座標というのが決まっているのですが、この座標とユーザが設定した$${3}$$つの値$${m,a,b}$$を使ってセル番号は計算されます。計算式は次のようになります。
座標$${ ( x , y ) }$$にあるセルのセル番号$${r}$$を計算する式:
$$
r = ( ax + by ) \bmod m
$$
ただし、この$${\bmod}$$というのは余りを計算する演算子です。例えば、$${m=5,a=2,b=3}$$のとき、座標$${ ( 2 , 4 ) }$$にあるセルの番号は、上の計算式に値を代入することで、
$$
r = ( ax + by ) \bmod m = ( 2 \cdot 2 + 3 \cdot 4 ) \bmod 5 = 16 \bmod 5 = 1
$$
というように計算できます。
ポリオミノを作る
さて、ここからユーザはセル番号を見ながらキャンバスのセルをクリックしてゆき、タイリング可能なポリオミノを形作ります。
では、具体的にどうやるのかを説明します。まず、各セルには、選択状態と非選択状態というものがあり、それはユーザが各セルをクリックすることで切り替わります。例えば、画像のようにしてセルをクリックしてみると、そのセルだけ色が変わるのが分かると思います。これがそのセルが選択された状態(アクティブな状態ともいう)です。
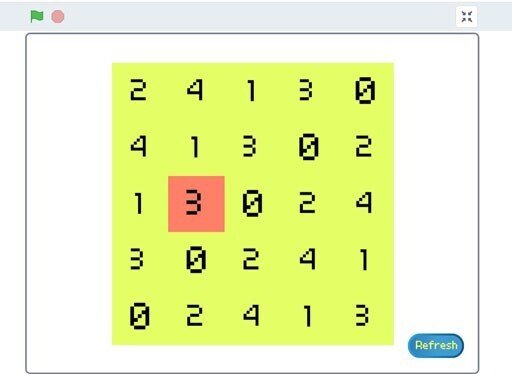
選択されたセルをもう一度クリックすると、色が元に戻ってそのセルは選択されていない状態(ニュートラルな状態ともいう)になります。
ユーザはこのようにしてキャンバスの中から$${m}$$個のセルを選択状態にして、それらのセルによってポリオミノを完成させます。ここで色んな形を試してみてください。画面右下にあるリフレッシュ(Refresh)ボタンを押すことでキャンバス上のすべてのセルが非選択状態になります。
例としてこのように選択してみました。

お気づきかと思いますが、選択されたセルをよく見てみると、セル番号が$${0}$$から$${m - 1}$$まで全部そろっています。実はここがポイントで、セル番号が重複していたり、欠けていたりするとアプリは次の段階に進めません。ここで疑問となるのが、
「そもそもキャンバスに$${0}$$から$${m - 1}$$までのセル番号が全て登場していなかったら?」
という点です。実はユーザの設定した$${m,a,b}$$の組み合わせによっては十分それも起こりえます。アプリ側でそういった設定をユーザがしないように防ぐ手立てもあったとは思うのですが、アプリのツールとしての側面と、教材としての側面の、二つの面を鑑み今回のバージョンではあえてそれはしませんでした。つまりユーザには適切な組み合わせを試行錯誤で見つけてもらうという方針で設計しています。具体的には、キャンバスに全てのセル番号($${0}$$から$${m - 1}$$まで)が登場しなかったら、緑の旗を押してアプリをリスタートしてもらうということになります。
タイリング画像の生成
$${0}$$から$${m - 1}$$のセル番号が付いたセルを選ぶことができたら、選択画面右下を見ると今までなかったタイリング(Tiling)というボタンが出現します。

ただし、アプリとしては、選択したセルがポリオミノであるかどうかについては判定していません。ここではただ$${0}$$から$${m - 1}$$のセル番号が付いたセルを選ぶことができたかどうかを見ています。ここでは、ユーザが選んだセルによってポリオミノができているという仮定で話を進めますが、このときタイリングボタンを押すと、そのポリオミノによるタイリング模様の繰り返しパターン($${m^2}$$)が生成されます。
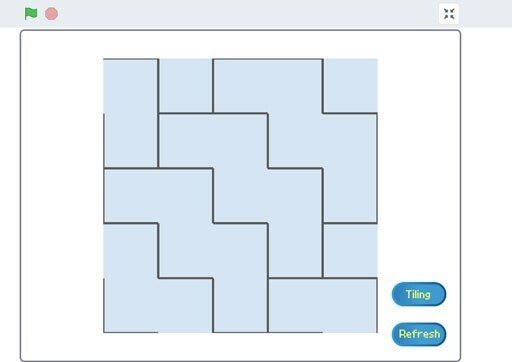
できた画像をスクリーンショットで保存するなどして、ご自身の作品にご利用ください。


(おわり)
