Scratchで学ぶ！ポリオミノ・パターンの世界～アルゴリズム編

2023年7月14日 15:35

みなさん，どうもこんにちは．C-Watcher開発担当の鈴木です．私が先頃作ったScratchアプリP.T.P.S.に関して，前回のチュートリアル編ではその使い方を紹介しましたが，今回はアルゴリズム編と題して，P.T.P.S.が利用しているアルゴリズムに焦点を当ててみようと思います．

やや技術的な内容になりますが，当該アルゴリズムを利用することにより，（P.T.P.S.を使わずとも）お手持ちの作図ソフト等でパターンを作成できるようになります．その他に，学習効果やメリットとしては，

P.T.P.S.の中を見たときに理解の助けになる．（Scratchで公開しているので，リミックス等が可能です．）
アルゴリズムを用いて独自のアプリを実装できる．（技術者向け）
ポリキューブを使った３D空間の充填法に応用できる．

などがあります．なお，３番目のポリキューブによる３D空間の充填法に関しては，いずれ機会があれば解説しようと思っています．また，アルゴリズムの証明に関しては，数学編にて解説する予定です．

正方形の数を決める

では，早速ですが始めたいと思います．私たちは今からポリオミノと呼ばれる正方形が辺でつながった図形を用いて，平面を埋め尽くすパターンを作ります．ただし，使うポリオミノは一種のみ，許されるタイルの操作は平行移動のみとします．

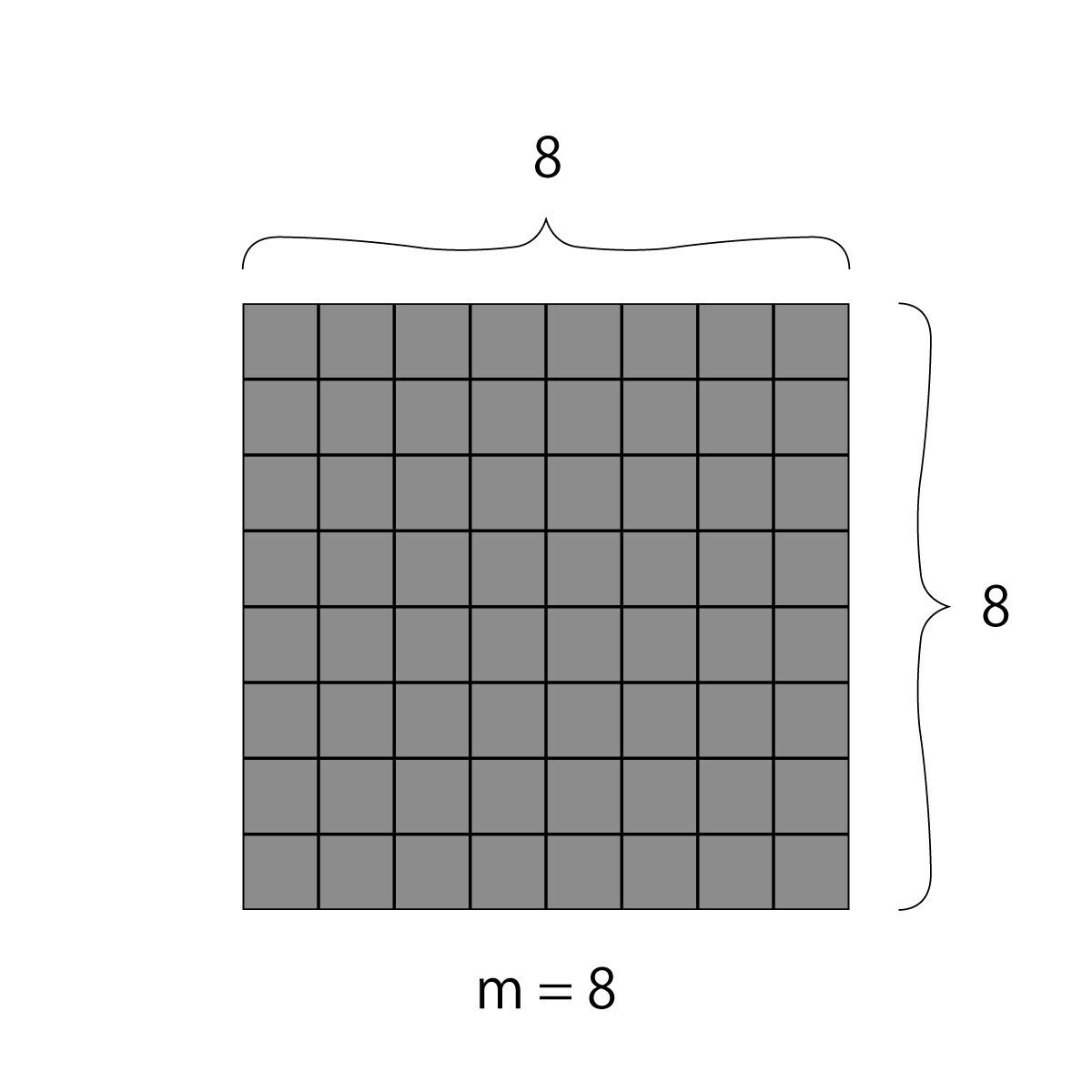
まず埋め尽くしパターンを作りたいポリオミノが何個の正方形で構成されるかを決めます．この正方形の個数は$${2}$$以上の整数であれば何でも構いません．では，ここではその数を$${m}$$とします．$${m}$$は$${2}$$以上である任意の整数であり，私たちがタイリングしたいポリオミノを構成する正方形の数です．

キャンバス

次に，一辺の長さが$${1}$$の正方形が縦，横にそれぞれ$${m}$$列ずつ並んだグリッドを用意します．私たちはこれからこの一辺の長さが$${m}$$の正方形の領域のことをキャンバス，キャンバスを$${m^2}$$個に分割する一辺の長さが$${1}$$の正方形のことをセルと呼ぶことにします．そして下記の手順を追ってこのキャンバスをポリオミノで埋め尽くすことにより，最終的にはこのキャンバスがタイリングの繰り返しパターンとなるようにします．

セル番号

では，まず各セルにセル番号というものを割り振ります．このセル番号というのは，キャンバスの各セルを$${m}$$色に色分けするためのもので，$${0}$$から$${m-1}$$までの整数の値をとります．各セルのセル番号を計算するためには，まず座標というものが必要になるので，その座標の決め方を以下に示します．

座標の決め方：

座標は$${０}$$から$${m-1}$$までの整数の順序対$${(x,y)}$$で表される．
一番左，一番下にあるセルの座標は$${(0,0)}$$で，この座標のことを原点と呼ぶ．
原点から$${x}$$右，$${y}$$上にあるセルの座標は$${(x,y)}$$．

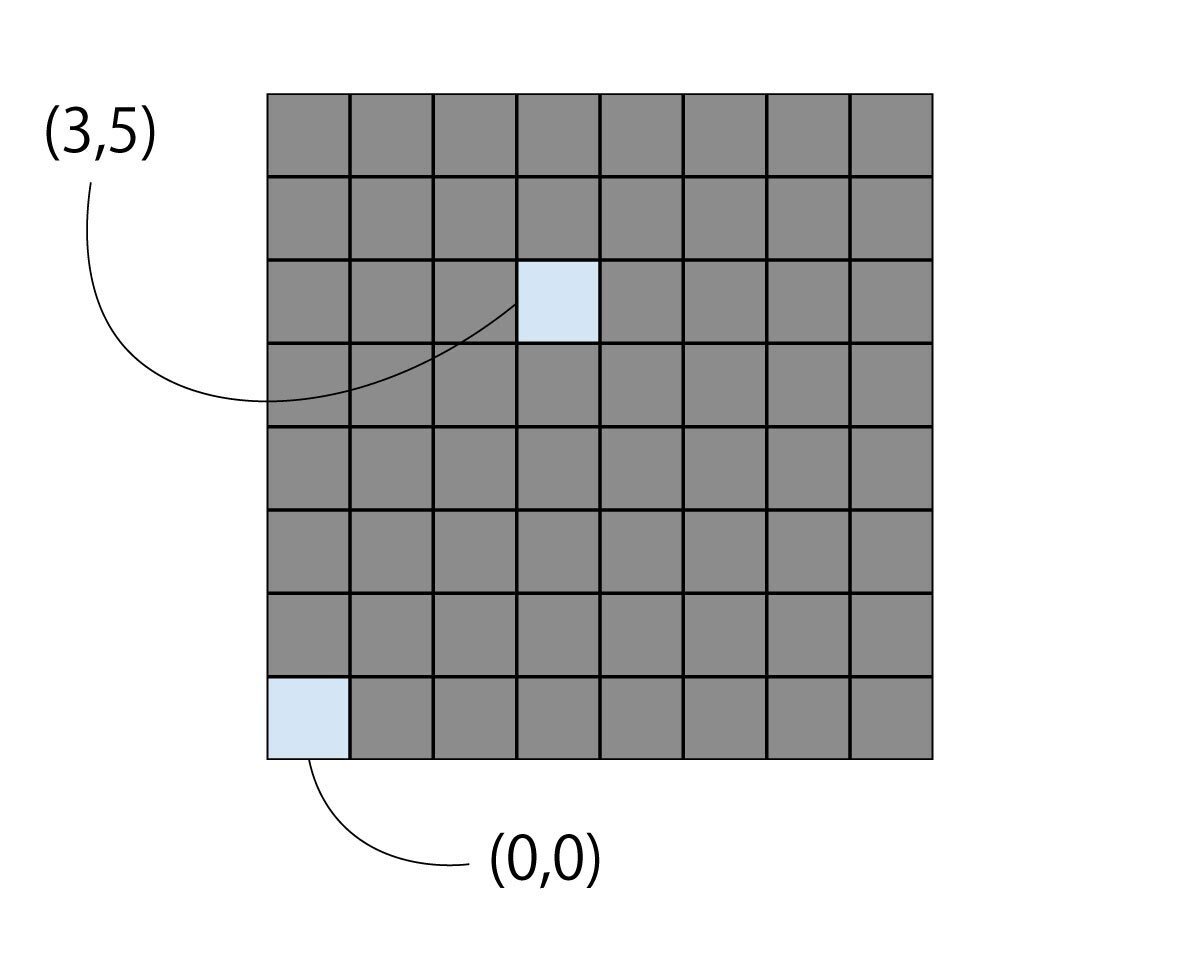
任意のセルについて，その座標$${(x,y)}$$が決まったら，そのセル番号$${r}$$を計算するには次のようにします．ただし$${\bmod}$$は除算の余りを計算する演算子です．

セル番号の計算式：

$$
r = (ax + by) \bmod m
$$

この計算式に登場する$${a,b}$$というのは，あらかじめ設定しておく必要があるのですが，次のようにします．

$${a}$$と$${b}$$は同時に$${0}$$ではない任意の整数．
$${a}$$と$${b}$$の最大公約数を$${d}$$とするとき，$${d}$$と$${m}$$が互いに素となる．（$${d}$$と$${m}$$の最大公約数が$${1}$$．）

この条件が成立するとき，かつそのときに限りセル番号として$${0}$$から$${m-1}$$までの整数が全てキャンバスに登場するので，私たちは続いての手順を実行することができます．例えば，$${a=3, b=6, m=8}$$のときは，$${3}$$と$${6}$$の最大公約数$${3}$$に対して，$${3}$$と$${8}$$の最大公約数が$${1}$$なので図のようにキャンバスには$${0}$$から$${7}$$までのすべての整数がセル番号として登場することになります．

ポリオミノを作成する

では，キャンバスのセルの中から好きなものを$${m}$$個選んでそれらがポリオミノを形作るようにします．ただし，選ばれたセルを見たときに，それらのセル番号が$${0}$$から$${m-1}$$まで全て揃っているようにします．つまり図（誤った選び方）のように重複していたり，欠けていたりしていないかを注意します．

私たちが作成したポリオミノのことをオリジナルと呼ぶことにします．キャンバスにはオリジナルのポリオミノが一つだけ置かれており，それがキャンバスを構成する$${m^2}$$個のセルのうち，$${m}$$個のセルを覆いかぶせている状態だと認識できます．

クローンを平行移動させる

私たちの次の目標はオリジナルを複製したクローンをいくつか作り，それらの平行移動によってキャンバス上の全てのセルを覆いかぶすことにあります．では，まずポリオミノに覆われていないセルのうち好きなものを選んで，それを$${p'}$$とします．オリジナルのポリオミノが覆うセルを見ると，必ず$${p'}$$とセル番号が一致するものがあるので，そのセルを$${p}$$とします．

今着目している二つのセル$${p}$$と$${p'}$$にはそれぞれ座標がありますが，$${p}$$の座標を$${(x,y)}$$， $${p'}$$の座標を$${(x',y')}$$とします．

そうしたら次に，オリジナルを複製したクローンを，オリジナルの位置から$${(x'-x,y'-y)}$$だけ平行移動させます．つまり回転させたり，裏返したりせずに，$${x'-x}$$右，$${y'-y}$$上に移動させます．クローンの一部がキャンバスからはみ出すこともありますが，その場合ははみ出した部分をトリミングします．