
C.Bさんの行った「右脳派・左脳派デュエリストアンケート」に関する詳細な統計分析と発展的考察に関する報告
こんにちは,TOYGER Pros所属のアキーシャです。普段は福岡でもそもそ遊戯王をやっている人です。
そんな私が以前参加した「遊ingトリオCS」という遊戯王の大会で,とあるアンケートをとっていらした方がいらっしゃいました。それが,「右脳派・左脳派とデュエリストのデッキ選択・好みについての関連性を見出す」という主旨のものでした。アンケートを実施していたのはC.Bさんという方です。
アンケートの説明があった時から中身に非常に興味があり,結果を楽しみにしておりましたところ,C.Bさんのnote記事が公開されました。
めちゃくちゃ面白い結果となっていますので,ぜひご一読ください。面白いだけではなく,本記事とは違い,グラフや表が豊富で,直感的にわかりやすいものとなっています!
ここに書かれていることでも,かなり十分に分析と考察がなされているな,と感じました。ですが,私は実は本業で研究論文を執筆するために,こういったアンケートの統計分析を行っています。こだわりが強いオタクなので,もっとこのデータ弄ってみたいという欲求に逆らえず,下記のようなツイートをしたところ…


なんとデータをいただけることになりました。たまげたなぁ。データを提供してくださったC.Bさん,そして取り次いでくださったTetsuさん,本当にありがとうございます!
というわけで,もう少し踏み込んだ統計分析を行い,C.Bさんの考察の説得力を増せるような論拠を提示したい,という想いのもと,この記事を執筆することにいたしました。
一応,統計のことがさっぱりの方にも,「へーこういう数字だから説得力があると言えるのかー」となんとなく理解していただけるような記述を心がけますが,数字がたくさん出てくるので,数字アレルギーの方はご注意を。面倒な式の話は極力省いて結果を紹介して参ります。それでは,よろしくお願いします。
1.本記事の目的
本記事では,C.Bさんが先述の記事内で述べていた考察をより補強するための材料として,統計的な数値を提示し,より説得力のある考察へと昇華させることを目的といたします。
2.本記事内で行う統計分析における仮説
統計分析を行う際には仮説が重要となります。そこで,今回はC.Bさんが記事内で主張されていた内容の一部を仮説として用い,その仮説を検証するために統計分析をしていく,ということにいたします。
3.分析の前に行ったデータの加工のお話
C.Bさんが記事内で紹介されていたようなグラフや表を用いた説明と,数値をいじくる統計分析とでは,データの加工の仕方が異なります。より具体的に言うと,「展開系・ミッドレンジ・コントロール」といった分類の用語を,すべて数値に置き換えるという操作になります。こうすることにより,日本語として入力されていたものを数字として処理し,分析にかけられる,ということになります。データをいただいて,まずはそのような加工を行いました。
4.右脳派・左脳派と大会での使用デッキに関して
4-1.群ごとのデッキ選択の傾向について
まず,「左脳派は展開系を使用した方が多く,右脳派は満遍なく」という主旨の考察がございましたので,ここから手をつけました。ひとまず以下のような表を作成しました。

ここで,ばらつきがあるかどうかを考える際の手法としては「適合度の検定」というものを行います。ざっくり言えば,この数字が偶然に起こるものか,それとも統計的に有効と言えるレベルでのものか(統計的に有意である,という表現を使います)を検証するものです。ここでは「カイ2乗検定」というものを行い,その数値を見るという手法を取ります。
4-2.カイ2乗検定について
カイ2乗検定とは,ある事象が起こる期待値と実際に測定された数値にズレがあるのか,そのズレは統計的に有意かを判断するために用いるものです。今回は,デッキ選択にばらつきがあるかどうかを考えたいので,ここでは一旦「右脳派・左脳派ごとに,デッキ選択にばらつきはない」という仮説を立てます。これを統計的に否定できるかどうかで考察が異なります。仮説が否定された場合,反対の意味となる「右脳派・左脳派ごとに,デッキ選択にばらつきがある」という仮説が支持される,ということになります。
※難しい言葉で,前者を「帰無仮説」,後者を「対立仮説」と呼びます。通常,帰無仮説に「自分にとって嬉しくない仮説」を置いて検定をします。
というわけで,ばらつきがないという仮説を一旦立てましたので,ばらつきがなかった時に期待される,期待値の表を作りました。

小数点以下は3桁で統一してみました。で,この期待値と実測値を使って計算を行います。手計算でやってもいいのですが,非常にめんどくさいので,今回はExcelの「CHISQ.TEST」という関数を使いました。
実際にどんな計算をするのか興味ある方は,「カイ2乗検定」で検索してみてください。シグマとか出てきますので苦手な方はご注意を。
CHISQ.TEST関数を使うと何がわかるのか。それは,"期待値と実測値のズレが,偶然に起こる確率がどれくらいか",ということです。つまり,出力された数字が1に近いほど,「偶然に起こりうる=意味があるとは考えにくいズレである」ということになり,この場合は帰無仮説が支持されます。反対に,1から遠い場合,「この数字は偶然ではない=何かしらの意味がある数値だ」ということになり,この場合は帰無仮説が棄却され,対立仮説が支持されます。
この,偶然かどうかの基準ですが,1%未満の確率であればかなり強い,5%未満であれば強い,10%未満であればまぁ偶然じゃ起こらんだろ知らんけど,くらいのイメージで偶然性を否定します。10%以上のものは全部偶然で,意味のある数字ではないとするのが統計学では一般的です。とても辛く厳しい世の中なのです。
4-3.カイ2乗検定の結果
さて,解説が長くなってしまいましたが,結果です。

というわけで,右脳派の数値は69.2%で偶然という結果となりましたので,この数字は統計的には有意ではありません。よって,帰無仮説が支持され,C.Bさんのおっしゃる通り,右脳派は満遍なくデッキを選択した,ということになります。
逆に左脳派は1.6%でしかこのような偏り方をしないという結果になりました。これはかなり強く偶然性を否定する結果です。研究論文書いてる時にこんなの出てきたらウキウキします。つまり,対立仮説が支持され,こちらもC.Bさんのおっしゃる通り,左脳派は何かしらの理由でデッキ選択をしており,このような数字の偏りが現れた,ということになります。
ここで重要となるのが”何かしらの理由”というところまでしか,数字では言及できない,ということです。あくまでも偶然性を検定しただけですので,その背景の理由はその都度考察する必要性があります。そのためには,C.Bさんが他にも様々なデータをとっておられる,環境に多いデッキの分布なんかも一緒に考慮していくのが良いです。こういった別データ,もしくは別期間で新たにとった今回と同様の調査データなんかを活用して,さらに考察を進めたり,別の切り口から調査をしたり…という作業の繰り返しが,研究活動というわけです。
4-4.群間の差を見てみることにする
ここからは,右脳派・左脳派との群間に差があるのかどうかを検定によって明らかにしたいと思います。群間の何かしらの差を検定する方法はいくつかありますが,今回は「マン・ホイットニーのU検定」というものを使います。「ウィルコクソンの順位和検定」などとも言われますが,出てくる数値は一緒です。名前が長くてめんどくさいので,この後は「U検定」と表記することにします。
4-5.U検定について
2つの群間に差があるかどうかを検定することができる手法です。冒頭の方で,デッキの分類を数字に変換したのは,この検定を用いるためです。
両群の回答の数字に,その数字が全体中の何位なのか,という順位をつけ,それを用いて計算をすることでUと定義される検定量を求めます。その検定量を定められた表に記載されている「限界値」というものと比較することで,2群間に統計的に有意な差があると言えるかどうか,を検討するという手法です。有意な結果が出れば対立仮説が支持され,有意でなければ帰無仮説が支持される,というのは,カイ2乗検定と同様となります。
今回は帰無仮説を「右脳派群と左脳派群の間には,デッキ選択の傾向に差はない」とし,対立仮説を「右脳派群と左脳派群の間には,デッキ選択の傾向に差がある」とします。
4-6.U検定の結果
まずはこんな感じでずらっと並べたデータに順位づけを行います。
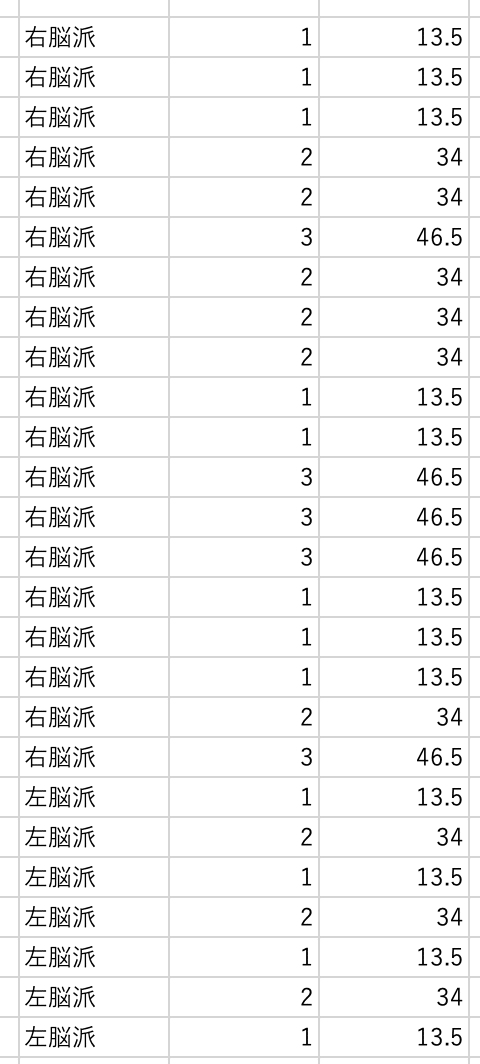
次にこれを元に各群の合計順位を求め,検定量Uを計算します。
計算するのですが,とにかくめんどくさい。そして計算した後もめんどくさい。あまりにも面倒なので,統計ソフトを使うことにします。今回は無料で使えるPSPPという統計ソフトを使いました。詳しい人なら,おや…?となる名前ですね笑
このPSPPは,ソフトに内蔵されている分析のほか,シンタックスに直接命令を入力することで,結果を出力してくれます。そんでもって,出た結果がこちら。

この有意水準の考え方も,カイ2乗検定の時と同様です。0.282とのことですので,28.2%の確率で今回の数字が偶然現れる可能性がある,ということですね。つまり,今回の結果だと,統計学的には帰無仮説が棄却できず,「右脳派・左脳派という群間で大会使用デッキの選択傾向に差はない」という結論に至ります。ちょっとしょんぼりする結果となってしまいました…
4-7.大会デッキ選択に関する結果のまとめと考察
しかし,統計的数字で否定されたからといって,意味のないデータ・分析であるというわけでは全くありません。むしろ,否定されたからこそ新たに生まれる考察というものもあります。
私は,今回の2種類の結果を受け,右脳派・左脳派のグループと大会シーンでのデッキ選択には以下のような傾向があるのではないかと推測します。
それは「右脳派・左脳派ともに,大会で勝つために合理的なデッキ選択をするが,その際の”合理的”の基準に何かしらの差があるのではなかろうか?」というものです。
根拠について説明します。まず,右脳派か左脳派かという群わけの間には,デッキ選択の傾向に差がないという結果が得られています。このことから,両群ともに,大会で勝つことを目的としてデッキ選択をしている傾向が強いことには,そんなに差がないと考えることができます。しかしながら,群ごとに見てみますと,デッキ選択の傾向に明らかに差があることが確認されました。ということは,「大会で勝つためにデッキを選択する」は共通でも「どのようにして勝つか」「どの選択が合理的で勝ちにつながるか」という選択基準に,右脳派と左脳派の違いが存在するのではないか,という仮説が立てられます。今回の調査ではこれはあくまで仮説・考察の域を出ませんので断言できませんが,楽しい考察ができる良い結果・データだなと個人的には思いました。C.Bさんに感謝です。
5.右脳派・左脳派と好きなデッキの傾向に関して
さて,C.Bさんが実施されたアンケートにはもう一項目の質問がありました。それは,「好きなデッキは何か」というものです。この設問は複数回答可能となっていました。ここのデータ加工が一番大変だったまであるほど,様々なデッキがフェイバリットデッキとして挙げられており,眺めていて楽しかったです。
5-1.右脳・左脳派と好きなデッキの分類
C.Bさんの執筆された記事に綺麗なものが載っておりますので,集計用に作成した簡易的なものを載せておきます。

ここからも,4.の項と同様の分析を行っていきます。
5-2.カイ2乗検定を用いた適合度の検定
まずはカイ2乗検定を使って,この数字の偶然性を検討します。必要な期待値表が以下のものです。

その後,この数字の偶然性をカイ2乗検定で確かめます。すると…

めちゃくちゃ強い偏りが出てますね〜,これはすごい。右脳派の数字が偶然に現れるのは0.3%,左脳派の数字の場合だと0.1%ということで,これはかなり強く有意差があると言える結果となりました。C.B.さんの記事内でも詳述されていましたが,好みの傾向に何かしらの偏りがあるとみて良い結果となりました。どのような偏りがあると捉えられるかについては,是非元記事の方をご覧ください!
https://note.com/cb_geargia/n/n0bd9c1e6041e
5-3.次に群間の差を見てみる
U検定を用いて群間の差を見てみることにいたします。今回は初っ端からツール,PSPPに頼ります。文明の利器は使ってなんぼです。
今回は帰無仮説を「右脳派群と左脳派群の間には,好きなデッキの傾向に差はない」とし,対立仮説を「右脳派群と左脳派群の間には,好きなデッキの傾向に差がある」とします。
そんでもって,得られた結果がこちら…

有意水準の数字が0.163とのことですので,16.3%,ということになりますね。これだと統計学的には有意とは言えない数字です…16.3%ならええやん!と私も思いますが,統計学の世界は辛く厳しいのです…ですので,こちらも大会選択デッキの時と同様に,「右脳派・左脳派という群間で好きなデッキの傾向に差はない」という結論となります。
しかし,これだとやはり適合度の検定の結果と矛盾しますね。ですので,ここにも考察の余地が生まれます。各群ごとで数値を見ると,明らかに偏りがあることが認められ,群間で見ると差が認められない,ということについて,今回の場合だと,「コントロールデッキの選択者が少ない」ということが1つの要因として挙げられると思います。おそらく,この傾向が右脳派群・左脳派群で似通っていたことから,群間での差が出なかったというのが,無視できない原因と言えるでしょう。
6.まとめと総合考察
最後に,得られた結果と知見のまとめをし,それらを合わせてどのような考察ができるかということを述べて終わりたいと思います。
・大会選択デッキにおいて,右脳派群は満遍なく,左脳派群は偏ったデッキ選択をした。
・大会選択デッキにおいて,群間ではデッキ選択に有意な差が認められなかった。
・好きなデッキにおいて,各群ともに何かしらの偏りがあることが認められた。
・好きなデッキにおいて,群間では好みの傾向に有意な差が認められなかった。
以上が統計分析によって得られた結果の簡単なまとめです。これらの結果と,アンケートを実施した環境とを踏まえて,私なりの考察をしてみます。
まず,大きな要因として,これを実施した対象者が,非公認の大会に集まったプレイヤーである,というのがあると思われます。つまり,最終的な選択には何かしら違いがあったとしても,その選択に至るまでには「大会で使用する」という共通の目的がある,ということです。ですので,その選択の基準には違いがあっても,全体としての傾向は似たものとなってしまったのかな,というような考察が可能となります。
それだと,好きなデッキのアンケートはどう説明するんだ,という話になりますね。これは結果からの推測・考察にすぎませんが,やはり好きなデッキのアンケートでも,これまでに大会プレイヤーとして使ってきたデッキを回答した傾向が強かったのではないでしょうか?そうであれば,いわゆる環境デッキや,その環境トップメタに抗うため,といった,大会シーンを想定した回答が多く集まりやすくなり,先ほどの考察と同様の傾向が得られることに説明がつきます。
もし今後,私が同様の調査を行う機会があるとすれば,非公認大会以外の場でも幅広くデータを収集してみたいです。そして,アンケートの項目に「普段どのような場で遊戯王をプレイすることが多いですか?」を追加してみます。これにより,対象者の属性をより細かく分類することができるからです。(ただし分析はクソめんどくさくなります)もしかしたら,その属性によって違いが検出されたりすると,イベント用に用意するデッキのヒントになるかもしれないな〜なんて妄想をしながら,このまとめを書いております。
以上で今回の考察を終えたいと思います。数字の並びだけでは明らかにならないことも見えてきて,個人的には非常に面白かったです。また,普段は自身の研究でしか使わず,望ましくない結果が出て台パンしながら嘆くばかりの統計ソフトを,趣味の分野で使うとこんなにも面白いのか…と新たな発見をすることができました。
ここまで読んでくださり,ありがとうございました。C.B.さんはたくさんのデータを載せて,いろんな考察をされている方ですので,もっと知りたい方はC.B.さんのnoteを色々と読んでみてください!
それではまた気が向いた時に〜
この記事が気に入ったらサポートをしてみませんか?
