【Tikz作品集】2直線のなす角
数学2「三角関数」の「加法定理」を利用して、2直線のなす角を求める問題のための図です。
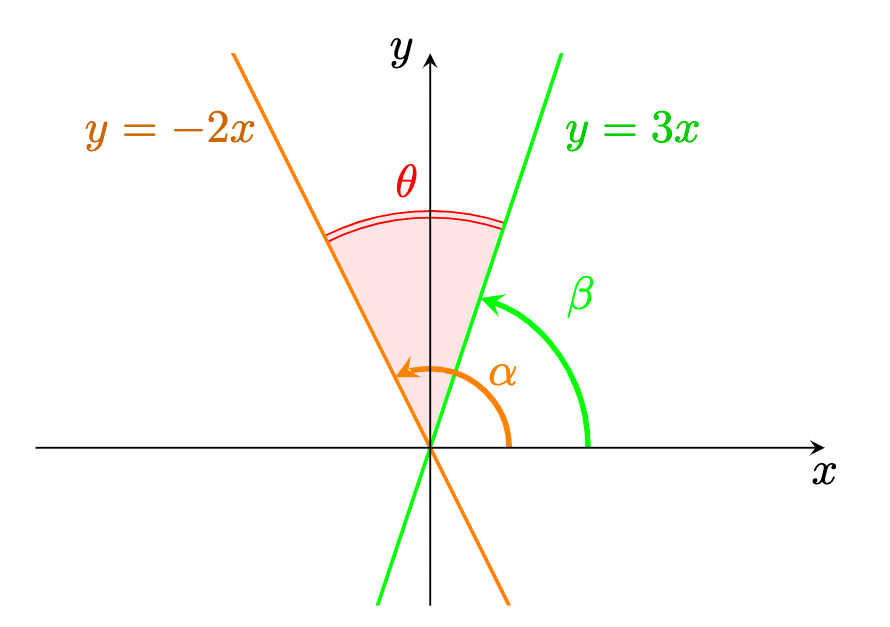
\documentclass[dvipdfmx,border=2mm,multi=pageSplit]{standalone}
\usepackage{tikz}
\usetikzlibrary{angles} %pic angle を使うため
\begin{document}
\begin{pageSplit}
\begin{tikzpicture}[scale=0.6]
\def\XMIN{-5}\def\XMAX{5}
\def\YMIN{-2}\def\YMAX{5}
\def\Ma{-2}
\def\Mb{3}
\coordinate (O) at (0,0);
\coordinate (A) at (-1,2);
\coordinate (B) at (1,3);
\coordinate (W) at (\XMAX,0);
\draw pic[draw=red, fill=red!10!white, angle radius=1.8cm] {angle=B--O--A};
\draw pic[draw=red, angle radius=1.75cm] {angle=B--O--A};
\draw[red] (95:3.4) node {$\theta$};
\draw[orange!80!black] (-2,4) node[left] {$y=\Ma{x}$};
\draw[green!80!black] (1.5,4) node[right] {$y=\Mb{x}$};
%% 関数のグラフ
\begin{scope}
\clip (\XMIN,\YMIN) rectangle (\XMAX,\YMAX);
\draw[orange, thick] plot (\x, \Ma*\x);
\draw[green, thick] plot (\x, \Mb*\x);
\end{scope}
\draw pic[->,>=stealth,draw=orange, angle radius=0.6cm, very thick] {angle=W--O--A};
\draw pic[->,>=stealth,draw=green, angle radius=1.2cm, very thick] {angle=W--O--B};
\draw[->,>=stealth] (\XMIN,0)--(\XMAX,0) node[below] {$x$};
\draw[->,>=stealth] (0,\YMIN)--(0,\YMAX) node[left] {$y$};
\draw[orange] (45:1.3) node {$\alpha$};
\draw[green] (45:2.7) node {$\beta$};
\end{tikzpicture}
\end{pageSplit}
\end{document}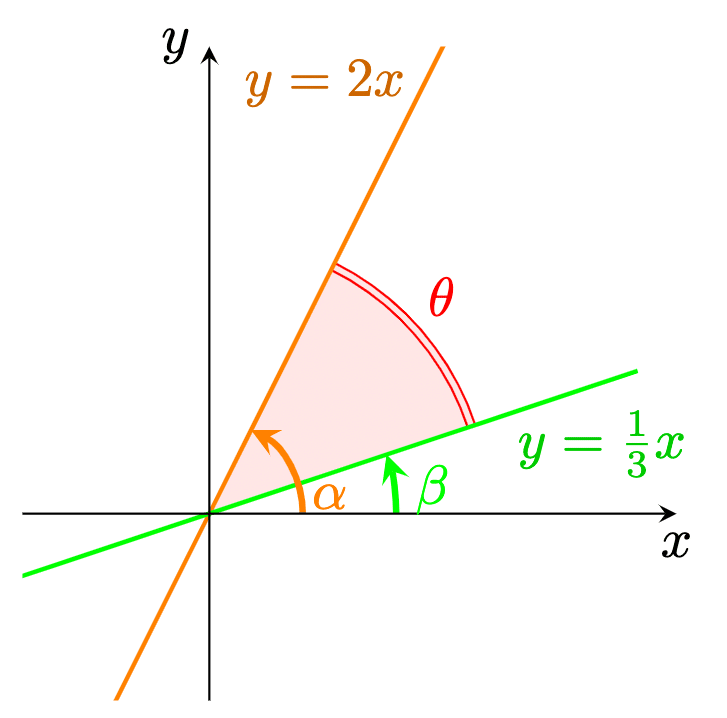
\documentclass[dvipdfmx,border=2mm,multi=pageSplit]{standalone}
\usepackage{tikz}
\usetikzlibrary{angles} %pic angle を使うため
\begin{document}
\begin{pageSplit}
\begin{tikzpicture}[scale=0.6]
\def\XMIN{-2}\def\XMAX{5}
\def\YMIN{-2}\def\YMAX{5}
\def\Ma{2}
\def\Mb{1/3}
\coordinate (O) at (0,0);
\coordinate (A) at (1,2);
\coordinate (B) at (1,1/3);
\coordinate (W) at (\XMAX,0);
\draw pic[draw=red, fill=red!10!white, angle radius=1.8cm] {angle=B--O--A};
\draw pic[draw=red, angle radius=1.75cm] {angle=B--O--A};
\draw[red] (43:3.4) node {$\theta$};
\draw[orange!80!black] (2.3,4.6) node[left] {$y=\Ma{x}$};
\draw[green!80!black] (4.2,1.3) node[below] {$y=\frac13x$};
%% 関数のグラフ
\begin{scope}
\clip (\XMIN,\YMIN) rectangle (\XMAX,\YMAX);
\draw[orange, thick] plot (\x, \Ma*\x);
\draw[green, thick] plot (\x, \Mb*\x);
\end{scope}
\draw pic[->,>=stealth,draw=orange, angle radius=0.6cm, very thick] {angle=W--O--A};
\draw pic[->,>=stealth,draw=green, angle radius=1.2cm, very thick] {angle=W--O--B};
\draw[->,>=stealth] (\XMIN,0)--(\XMAX,0) node[below] {$x$};
\draw[->,>=stealth] (0,\YMIN)--(0,\YMAX) node[left] {$y$};
\draw[orange] (8:1.3) node {$\alpha$};
\draw[green] (6:2.4) node {$\beta$};
\end{tikzpicture}
\end{pageSplit}
\end{document}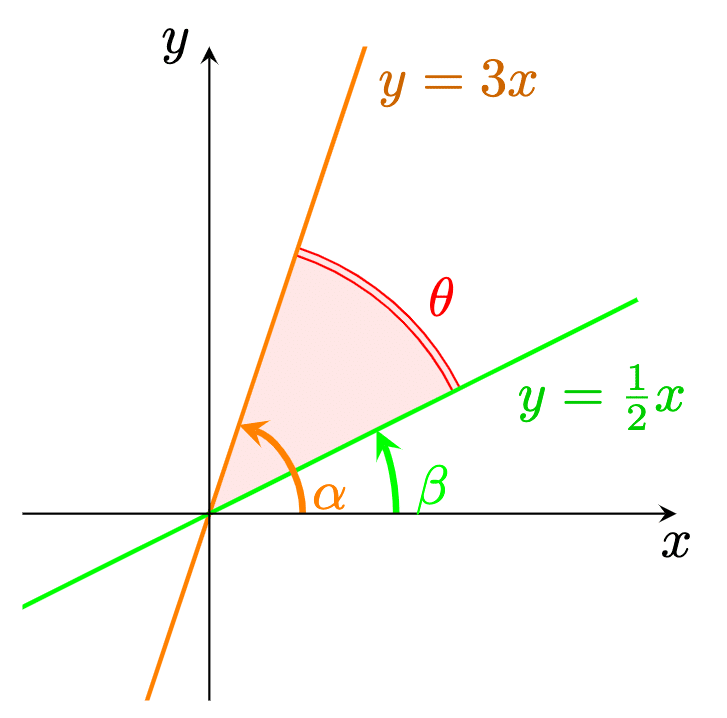
\documentclass[dvipdfmx,border=2mm,multi=pageSplit]{standalone}
\usepackage{tikz}
\usetikzlibrary{angles} %pic angle を使うため
\begin{document}
\begin{pageSplit}
\begin{tikzpicture}[scale=0.6]
\def\XMIN{-2}\def\XMAX{5}
\def\YMIN{-2}\def\YMAX{5}
\def\Ma{3}
\def\Mb{1/2}
\coordinate (O) at (0,0);
\coordinate (A) at (1,3);
\coordinate (B) at (1,1/2);
\coordinate (W) at (\XMAX,0);
\draw pic[draw=red, fill=red!10!white, angle radius=1.8cm] {angle=B--O--A};
\draw pic[draw=red, angle radius=1.75cm] {angle=B--O--A};
\draw[red] (43:3.4) node {$\theta$};
\draw[orange!80!black] (1.6,4.6) node[right] {$y=\Ma{x}$};
\draw[green!80!black] (4.2,1.8) node[below] {$y=\frac12x$};
%% 関数のグラフ
\begin{scope}
\clip (\XMIN,\YMIN) rectangle (\XMAX,\YMAX);
\draw[orange, thick] plot (\x, \Ma*\x);
\draw[green, thick] plot (\x, \Mb*\x);
\end{scope}
\draw pic[->,>=stealth,draw=orange, angle radius=0.6cm, very thick] {angle=W--O--A};
\draw pic[->,>=stealth,draw=green, angle radius=1.2cm, very thick] {angle=W--O--B};
\draw[->,>=stealth] (\XMIN,0)--(\XMAX,0) node[below] {$x$};
\draw[->,>=stealth] (0,\YMIN)--(0,\YMAX) node[left] {$y$};
\draw[orange] (8:1.3) node {$\alpha$};
\draw[green] (6:2.4) node {$\beta$};
\end{tikzpicture}
\end{pageSplit}
\end{document}