波紋を思い描く　その２

水面の変位は速度ポテンシャルを用いて表せるので、速度ポテンシャルを求めたい。

円筒座標と変数分離

(10)より

(18)

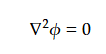
中心から広がる波を扱うので円筒座標を採用する。

Fig.3

円筒座標でのラプラシアンを用いて(18)は以下となる。

(19)

Φをr、θ、zと時間tの関数とし、変数分離する。

(20)

(19)に代入する。

(21)

式の分離１

以下のように2式に分離する。

(22)

(23)

(22)は以下のような2階の微分方程式なので

(24)

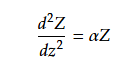
一般解は

(25)

となる。ここで水底をz=0として

Fig.4

水底でのz方向の速度を0とする。

(26)

これはz=0で(25)の微分が0である必要がある。

(27)

ここで

(28)

より

(29)

とする。
Zは以下となる。

(30)

次に(23)を以下のように変形する。

(31)

式の分離２

これも2式に分離する。

(32)

(33)

(33)から着手する。

(34)

θ方向に整数次の振動を与えたい。

(35)

(36)

θ方向の解を以下とする。ここでは次数毎の係数は設けない。

(37)

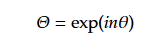
(32)は(35)を用いて

(38)

となる。 (38)のαが1になると都合がよい。そこで以下のように変数を変換する。

(39)

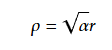
これを用いると

(40)

であり、 (38)は

(41)

となり、Besselの微分方程式を得た。

(41)は次数毎に解を持つ。

(42)

Neumann関数は原点で発散するので

(43)

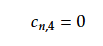
とする。
(30) (37) (42) (43)より速度ポテンシャルは以下となる。

(44)

(45)

その３に続く