
株価はランダムなのか? その4
前項で確率密度関数は対数正規分布となった。

例えばD=0.05、$${s_0}$$=1000としてt=0.1, t=1, t=5をグラフにすると以下のように時間の経過と共にピークが左側に移動するなだらかな山になる。

ここでは期待値、中央値、最頻値を求める。
期待値
期待値は確率密度に株価をかけたものを領域全体で積分した値となる。

ここで

とすると

であるので、 (36)は

になる。
(39)のexpの中を以下のように変形する。

(39)に代入して期待値は以下となる。

中央値
確率密度を積分して1/2になる位置が中央値となる。

(37) (38)を用いて

であるので中央値は以下となる。
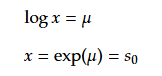
最頻値
確率密度関数が極大となる位置が最頻値である。
(35)をsで微分する。

よって

より最頻値は以下となる。

まとめ
以上をまとめると

で

となる。
え!? なんかおかしい。
期待値が初期値を上回っている。株を買うと儲かるんか!?
その5に続く
