
ガリレオの式、湯川先生の頭の中 その2
前項で二つのスカラーポテンシャルがHelmholtz方程式を満たすことが分かった。二つのスカラーポテンシャルで電場・磁場を表せるので、二つのスカラーポテンシャルが分かれば電場・磁場を特定できる。


ここでは微分方程式の解を級数で表すことになるので、湯川先生が学生に日常的に講義していることに近いかもしれない。
変数分離
一般化して以下を解くことにする。

(32)に$${r^2}$$をかける。

スカラーポテンシャルを変数分離する。

(34)を(33)に代入する。
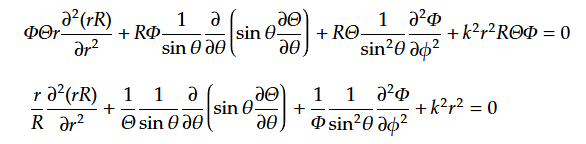
分離定数αを用いて(35)を2式に分離する。
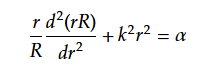

(37)を更に分離定数βを用いて2式に分離する。


(39)は

で一価の関数とするためβは

として、 (40)は以下となる。

(41)を用いて(38)は

となり、一価の関数とするためαは

として、 (43)は以下となる。
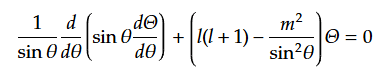
また(44)を用いて(36)は

となる。
(42)(45)(46)によりスカラーポテンシャルは各方向の関数、方程式に分離できた。
φ方向
(42)の一般解は

となる。
θ方向

とすると

であるので(45)は

となる。これはLegendreの陪微分方程式であるので、ここでは解をLegendre陪関数とする。最終的に他の方向と掛け合わせるので、ここでは係数は設定しない。

r方向

として以下の関数Zを定義する。

(50)(51)を用いると(46)は以下になる。
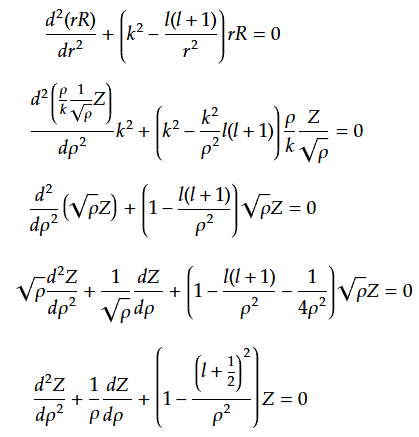
これは半整数次のBesselの微分方程式である。Bessel関数をJ、Neumann関数をNとして一般解を以下のように一次結合で表す。ちょっと先走るがHankel関数を想定してNeumann関数にiを掛けておく。$${c{_3}}$$、$${c{_4}}$$は複素数として考えてよいので特にiを付ける必要はないが。

(26)~(31)はスカラーポテンシャルにrをかけた値を使用しているので、どこかでrをかける必要がある。よってここではRではなくrRをZを用いて表すと

ZはBessel関数とNeumann関数の一次結合で表せたが、 (54)の

は球Bessel関数と球Neumannの一次結合であり、 (54)の

はRicatti-Bessel関数とRicatti-Neumann関数の一次結合である。よってψをRicatti-Bessel関数、χをRicatti-Neumann関数とすると

となる。
スカラーポテンシャル
以上で各方向の関数が得られた。 (41)(44)より解は次数を持つため級数となる。 (34)より各方向を統合して

を得た。
「来月の変数分離の講義でこれを入れてみるか」などと一瞬雑念が入るかもしれないので、湯川先生の頭の中でここまで6秒くらいだろう。
その3に続く
