コーヒーは踊る　その１

以前の記事でコーヒーに角砂糖を落とした時のコーヒー表面の動きを再現した。
　麗しのコーヒー　その１
　麗しのコーヒー　その２

今回はカップを動かした時の動きを再現してみたい。

congerdesign, pixabay.com

支配方程式

角砂糖を落とした時との違いは外力が重力以外に水平に加わることである。それ以外は同じであるとする。

支配方程式は従来と同じくNavier-Stokes方程式と連続の式とする。

(1)

(2)

前提として非圧縮、渦なし、速度の二次成分無視、とする。速度ポテンシャルを

(3)

とすると、以下を得る(参照：波紋を思い描く　その１)。

(4)

(4)から∇を消したいので積分する。ただし水平外力による加速度は面内で一定とする。

(5)

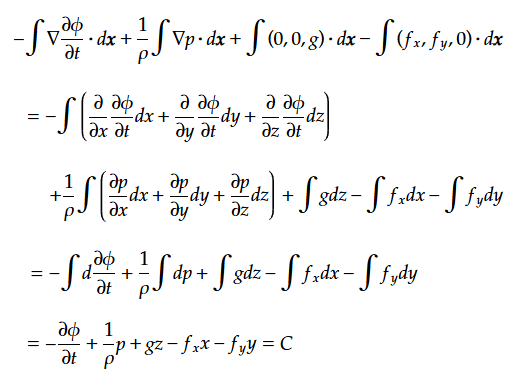
コーヒー表面を考える。基準位置からのz方向の変位をηとする。

Fig.1

コーヒー表面での圧力pは大気圧$${p_0}$$​に等しい。また大気圧$${p_0}$$は一定である。

Fig.2

(5)の第三項は位置エネルギーに相当するのでzは変位に置き換えられ、圧力は一定であるので以下となる。

(6)

変数分離

(2)(3)より

(7)

である。円筒座標で変数分離して

(8)

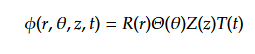
円筒座標のラプラシアンで表すと

(9)

となる。各方向の方程式に分離するが、「波紋を思い描く　その２」と同じであるため省略する。最終的に以下となる。

(10)

(11)

境界条件

「麗しのコーヒー　その１」と同じになるが、再度記載する。

Fig.3

カップの半径を$${r_a}$$で一定とする。カップの壁面でr方向の速度は0になるので

（12）

(11)より

(13)

となればよい。「波紋を思い描く　その２」の (39)を用いて

(14)

となるので、Bessel関数を微分して0になる点を見つければよい。
n次のBessel関数の微分の正のm番目の零点を$${λ_{m,n}}$$として分離定数$${α_m,n}$$は

(15)

となる。次数nだけでなくBessel関数の微分の零点の番号を表すmが新たに追加される。これは径方向の波の重ね合わせに相当する。

「波紋を思い描く　その２」の(39) 、(10) (11) (15)より速度ポテンシャルは

(16)

となる。

時間微分

(6)をtで微分して

(17)

Tを掛けて以下のTの時間の二階の微分方程式を得る。

(18)

よってTは第3項が0の場合の一般解と特殊解の和になる。第3項が0の場合は角砂糖の場合と同じく以下となる。

(19)

(20)

Hは基準位置からカップの底までの深さである。Hは一定、変位はHと比べて十分小さいとしている。

Fig.4

t=0のときの変位をf(r,θ)、変位方向の速度を0として

(21)

(22)

(23)

となる。

特殊解

次に特殊解を求める。ここでは水平外力による加速度はx方向、y方向ともに単振動、角速度をωとする。

(24)

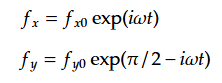
(18)に代入して特殊解を求めると

(25)

となる。

時間成分に水平外力による影響を追加

(25)と一般解である(19)と加えたいが、(19)は級数展開されている。そこでx,yを同様に級数展開する。

θ方向にFourier級数展開、r方向に第二種Fourier-Bessel級数展開(Dini展開)をし以下を得る。

(26)

(27)

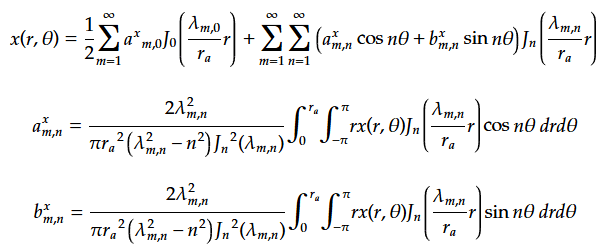
(21)の右辺の第1項と第2項の時間成分に(25)で得た特殊解を(26)(27)を用いて加える。
第1項:

(28)

第2項:

(29)

水平外力による加速度の項を追加

(6)より

(30)

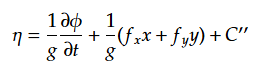
右辺の定数項は(21)の第3項と第4項に相当する。右辺第2項は(24)(26)(27)より

(31)

となる。

以上よりコーヒー表面の変位は以下となる。

(32)

これまでに付けた条件

• 非圧縮

• 渦なし

• 速度の二次成分は無視

• カップの壁面で径方向の速度は0

• カップの径は一定

• 変位は深さに対して十分小さい

• 深さは一定

• 水平外力なしの一般解において時刻0で変位方向の速度は0

• 水平外力による加速度は面内で一定

• 水平外力による加速度はx方向、y方向ともに単振動

参考文献

[1] 森口繁一・宇田川銈久・一松信，岩波数学公式Ⅱ 級数・フーリエ解析，岩波書店，1987.
[2] Watson, George N., A Treatise on the Theory of Bessel Functions Second Edition, Cambridge University Press, 1944.

その２に続く