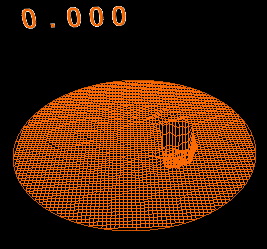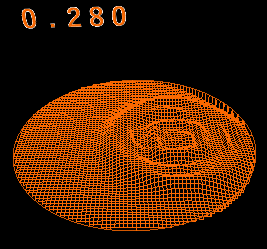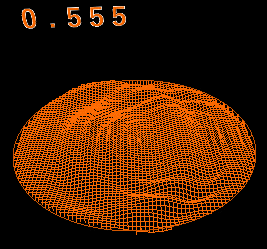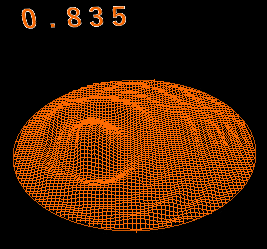
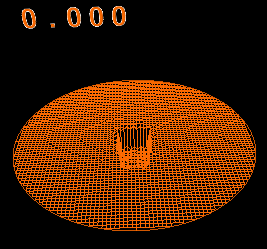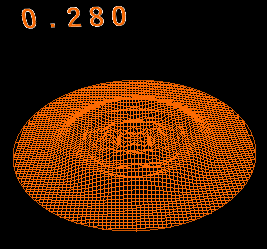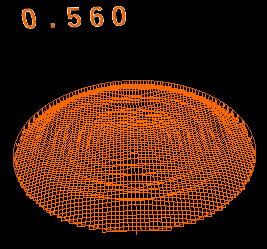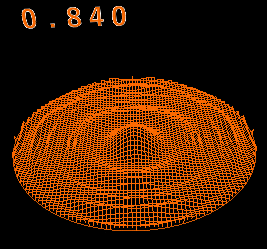麗しのコーヒー その2
前項の残件である級数の係数および定数を求めればコーヒー表面の動きが分かる。

初期条件
(63) (65)よりt=0のときの変位を以下とする。f(r,θ)は既知とする。

θ方向にFourier級数展開、r方向に第二種Fourier-Bessel級数展開(Dini展開)を考える。
定理:
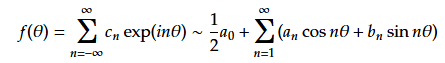




(66)には級数の係数および定数が含まれていて、級数展開して「波紋を思い描く その4」のように単純に係数を比較するいうわけにはいかない。そこで一旦、定数C''を無視した以下を考える。

(67) (70)を用いて(72)を以下とする。係数$${c'_{m,n}}$$の代わりに$${a'_{m,n}}$$,$${b'_{m,n}}$$を用いる。

(68) (69) (71)より係数は以下となる。


これで係数が得られ、定数C''を無視した級数展開ができた。しかし変位の変化は追えるが相対的な値であって絶対的な値とはならない。そこでC''を加えて、C''を求める。

(76)を0≦r≦$${r_a}$$, -π≦θ≦πで積分する。

よって定数C''は以下となる。
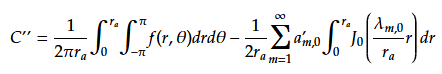
以上より変位は、以下で与えられる。

これまでに付けた条件
非圧縮
渦なし
速度の二次成分は無視
カップの壁面で径方向の速度は0
カップの径は一定
変位は深さに対して十分小さい
深さは一定
時刻0で変位方向の速度は0
参考文献
[1] 森口繁一・宇田川銈久・一松信,岩波数学公式Ⅱ 級数・フーリエ解析,岩波書店,1987.
[2] Watson, George N., A Treatise on the Theory of Bessel Functions Second Edition, Cambridge University Press, 1944.
麗しのコーヒー表面を描く
初期値f(r,θ)を決めて(74) (75)で係数、(78)で定数を求めて、 (79)で計算するだけ。解析的にコーヒー表面の動きが分かる。
波紋の場合と同様に人手での計算は厳しいのでPCを使う。 (74) (75) (78)の積分はGauss-Legendre積分を使う。
計算例
直径8cmのマグカップに深さ8cmでコーヒーが入っている。
そこに1x1x1cmの角砂糖を落として角砂糖の形の穴ができたとする。