
江戸のオタク
大昔から世界中にオタクはいたと思う。ここでいうオタクとは他人から見たら大して意味がないことに病的に熱中する人のこと。ぱっと思いつくのが実用数学を超えたマニアックな数学として発展した江戸時代の和算の世界の人々。それ何の役に立つの?って言われそうなものに熱中していたと思う。
江戸の激ムズ問題
日経サイエンスの2025年1月号に載っていた和算家の関孝和の記事が面白かったので関連する内容を書いておきたい。関孝和と弟子の建部賢弘が1683年に出版した研幾算法には49題の問題と解答が掲載されていたが、その中のずば抜けて難しい問題が以下らしい。

直径1の円の弧と弦に囲まれた部分の面積を求めるというもの。扇から三角形部分を引けばよいので

となる。特に難しくないと思うが、関の時代には三角関数が使えなかったのでこんなに簡単にはいかない。更に答えが無理数になる場合は近似で表す必要がある。
答え
関・建部の回答は面積をSとすると以下とのこと。

なんじゃこりゃ?というレベルで複雑な式だが、xとaを入力してできる二次方程式の解が求める面積となる。当時でも一元の高次方程式は解けたのでこれで面積が得られる。誤差がどれくらいあるのかというと以下のようになる。

xが極端に小さくなければ誤差は0.1%未満になっている。コンピュータも三角関数表もなかった時代の答えとしては驚異的な精度だと思う。
どうやって解いたのか
記事によると関の時代でも、三平方の定理、連立一次方程式、多項式近似、一元の高次方程式はあったらしい。これらを駆使して解いたと思われる(研幾算法には答えしかなく、途中経過が掲載されていない)。
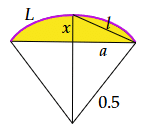
弧の長さをL、半分の弧の弦の長さをlとする。Sと三角形と扇の関係から

となる。Lが分かればSが求まる。ここでLは内接する多角形の辺の長さで近似して、更に三平方の定理を使うので二乗になっていると都合がよい。そこで(3)を二乗する。

Lの二乗をlの二乗の多項式で近似できればよい。Fig.2を率でなく差の値そのものとすると以下になる。

誤差が極端に小さいところが6箇所ある。この点を使って多項式近似したと思われる。

lはxとaで表す。

Fig.3の下の直角三角形を使うと

であるので(6)は

となり、lの二乗はxに等しくなるので(5)は以下となる。
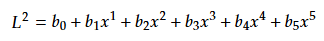
Fig.4の6箇所は

で、これらと近似的に求めたLの二乗を代入して連立一次方程式を作り、(9)の$${b{_0}}$$~$${b{_5}}$$を求める。

求めた$${b{_0}}$$~$${b{_5}}$$は無理数になるので近似分数で表してから、 (4) (9)に代入して

を得る。誤差を計算すると関・建部の結果とほぼ同じになった。

もう少し考えてみる
以上が日経サイエンスの記事をもとに計算してみた結果だがモヤモヤが少しある。 (2)と(12)の係数を比較するとx,aの次数が異なる。素直に考えるとaまたはxの出現を抑えるようにすると思うが (2)はそうはなっていない。

天下り的に考えると、理由は分からないが関・建部はLの二乗の多項式近似を(5) (9)ではなく、以下のようにしている。これでも出来るがちょっと変則的な感じがする。

上記と同様に$${b{_0}}$$~$${b{_5}}$$を求めることができるので(4)に代入して16と$${x{^5}}$$を掛けて整理すると以下となる。

近似分数部分は同じにはならないが係数のx,aの次数は揃った。数値を入れて誤差を比較すると以下のようになる。これも関・建部の結果とほぼ同じになった。

関・建部がより面倒だと思われる多項式を使った理由は分からないが、大量の労力をつぎ込んで計算方法を考えて計算したのは確かだと思う。ふつうはこんな計算は絶対にやりたくない。他の和算家たちに向けて「解けるものなら解いてみな!」という感じに自分たちの成果を見せつけているのかもしれない。同時代の一般の人たちから見たら何をやっているのかすら不明だったと思われる。
面積を求めるような場面がどれ程あるのか不明だが、ここまで頑張って精度を高める必要があるとは思えない。オタク故の行動なんだろう。関や建部は記録が残っている有名人だが、記録が残っていない無数のオタク達が様々なものに熱中してきたはず。オタクの熱量はいつの世もすごい。
