ガリレオの式、湯川先生の頭の中　その４

いよいよクライマックスだ。前項で入射成分のスカラーポテンシャルを得た。ここでは散乱成分と球の内部のスカラーポテンシャルを考える。前述の通りスカラーポテンシャルは(56)で与えられる。

(56)

内部と散乱のスカラーポテンシャル

$${χ_l}$$は原点で発散するので球の内部で用いるのは適切ではない。よって球の内部では$${c'_{3,l}}$$=1、$${c'_{4,l}}$$=0とする。

散乱成分では無限遠方で電場、磁場を0にしたい。そこでRicatti-Bessel関数とRicatti-Neumann関数の一次結合を$${c'_{3,l}}$$=1、$${c'_{4,l}}$$=±1としてRicatti-Hankel関数とする。

(88)

$${ζ^{(1)}_{l}}$$は第1種Ricatti-Hankel関数、$${ζ^{(2)}_{l}}$$は第2種Ricatti-Hankel関数である。時間振動をexp(-iωt)として空間方向を正にしているのでここでは第1種Ricatti-Hankel関数を用いることにする。以下では$${ζ_{l}}$$は第1種Ricatti-Hankel関数とする。

入射波でm=1、l≧1としている。また$${c_{1,m}}$$,$${c_{2,m}}$$を入射波にならい球の内部と散乱成分のスカラーポテンシャルを以下とする。

(89)

(90)

(91)

(92)

境界条件

球の表面r=aで電場と磁場の接線方向であるθ、φ方向の成分が球の内外で連続であるとする。

(93)

前述の以下の(27)(28)(30)(31)

(27)

(28)

(30)

(31)

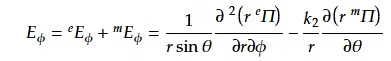
と(93)を用いて電場と磁場θ、φ方向の成分が球の内外で連続であるとすると

がr=aで連続である。よって以下が成り立てばよい。

(94)

(95)

(96)

(97)

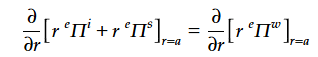
以下の$${ψ'_{l}()}$$,$${ζ'_{l}()}$$は引数での微分とする。
(94)(79)(89)(91)より

(98)

(95)(87)(90)(92)より

(99)

(96)(79)(89)(91)より

(100)

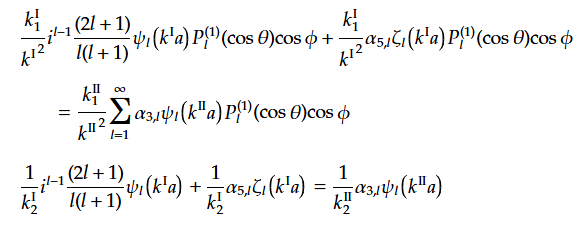
(97)(87)(90)(92)より

(101)

ここで

(102)

とすると(98)(99)(100)(101)は以下となる。

(103)

さらに

(104)

とし、 (57)より

(105)

であるので、 (103)は以下となる。

(106)

未知数$${a_{l}}$$, $${b_{l}}$$, $${c_{l}}$$, $${d_{l}}$$を求める連立一次方程式に帰着された。 (106)を解いて

(107)

(108)

(109)

(110)

になる。これで材料は揃った。

球の内部の電磁波

前述の式および$${c_{l}}$$, $${d_{l}}$$を用いて球の内部の電磁波を決定する。表記を簡単にするため、Legendre陪関数に関連して以下を定義する。

(111)

(26)(89)(102)より

(112)

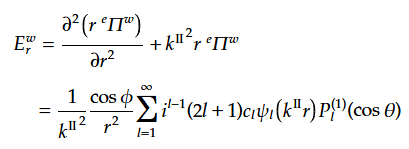
(27)(89)(90)(102)(111)より

(113)

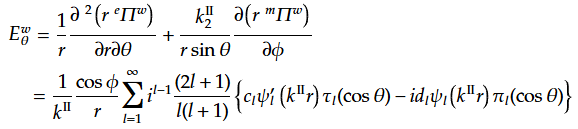
(28)(89)(90)(102)(111)より

(114)

(29)(90)(102)より

(115)

(30)(89)(90)(102)(111)より

(116)

(31)(89)(90)(102)(111)より

(117)

$${c_{l}}$$, $${d_{l}}$$は(109)(110)を参照。

計算はこれで終わり。湯川先生の頭の中でここまで14秒くらいだろう。

その５に続く