ガリレオの式、湯川先生の頭の中　その３

前項でスカラーポテンシャルの級数展開を得た。ここからいよいよ人間の頭と電磁波の関係を考えていく。幻聴が起きるのは人間の頭に電磁波が当たることによる影響だと湯川先生は考えたはずだ。

Fig.1

人間の頭を均一な球だと仮定する。球の半径をaとして、球の内外の物性を以下とする。

Fig.2

(57)

スカラーポテンシャルを球の外部（入射、散乱）と球の内部に分ける。

Fig.3

入射波

Fig.4

入射波はz方向に伝播し、電場がx方向、磁場がy方向に偏光している既知の平面波とする。電場の振幅を1とする。

r方向成分は

(58)

(59)

となる。ポテンシャルを用いて表すと、 (26)(29)より

(60)

(61)

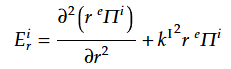
である。よって(58)と(60)、 (59)と(61)は等しくなるはずである。

ちょっと脇道

(60)(61)はRicatti-Bessel関数やLegendre陪関数を使うので、そのための準備のため脇に逸れる。公式から使う式を導く。
$${j{_n}}$$を球Bessel関数、$${P{_n}}$$をLegendre多項式として

(62)

である。$${ψ{_n}}$$をRicatti-Bessel関数として

であるので(62)は

(63)

となる。

zを複素数として

(64)

である。m=1として

(65)

xを[-1,1]の実数として

(66)

ここで$${x=cosθ}$$として

(67)

となる。

入射波の級数展開

さて本流に戻ろう。 (58)(59)の指数関数部分に着目する。
(63)を用いて

(68)

θで微分して

(69)

(58)に代入して

(70)

(67)を用いて

(71)

となる。

であるので(71)は

(72)

となる。

一方、 (56)を用いてスカラーポテンシャルは

(73)

である。(72)との次数の比較からm=1、$${c_{2,m}}$$=0である。またRicatti-Neumann関数は使われないため$${c'_{4,l}}$$=0である。よって

(74)

とする。 (74)を(60)に代入する。

(75)

前出の(46)の解の一つが$${ψ{_l}}$$である。

(46)

(76)

(76)より

(77)

であるので(75)に代入して

(78)

(74)(78)より

(79)

を得る。

ここまで電場を起点して(70)～(79)まで計算してきた。磁場を起点にしても同様である。 (59)(69)より

(80)

(67)を用いて

(81)

となる。

であるので(81)は

(82)

となる。

一方、 (56)を用いてスカラーポテンシャルは

(83)

である。(82)との次数の比較からm=1、$${c_{1,m}}$$=0である。またRicatti-Neumann関数は使われないため$${c'_{4,l}}$$=0である。よって

(84)

とする。 (84)を(61)に代入する。

(85)

(77)を(85)に代入して

(86)

となるので(84)(86)より

(87)

を得る。

(79)(87)より入射成分のスカラーポテンシャルが得られた。次項以降で散乱および球の内部のスカラーポテンシャルを求める。

湯川先生の頭の中でここまで10秒くらい。

その４に続く