円と円の当たり判定

まずは、円同士の当たり判定について書いていきます。

判定の取り方

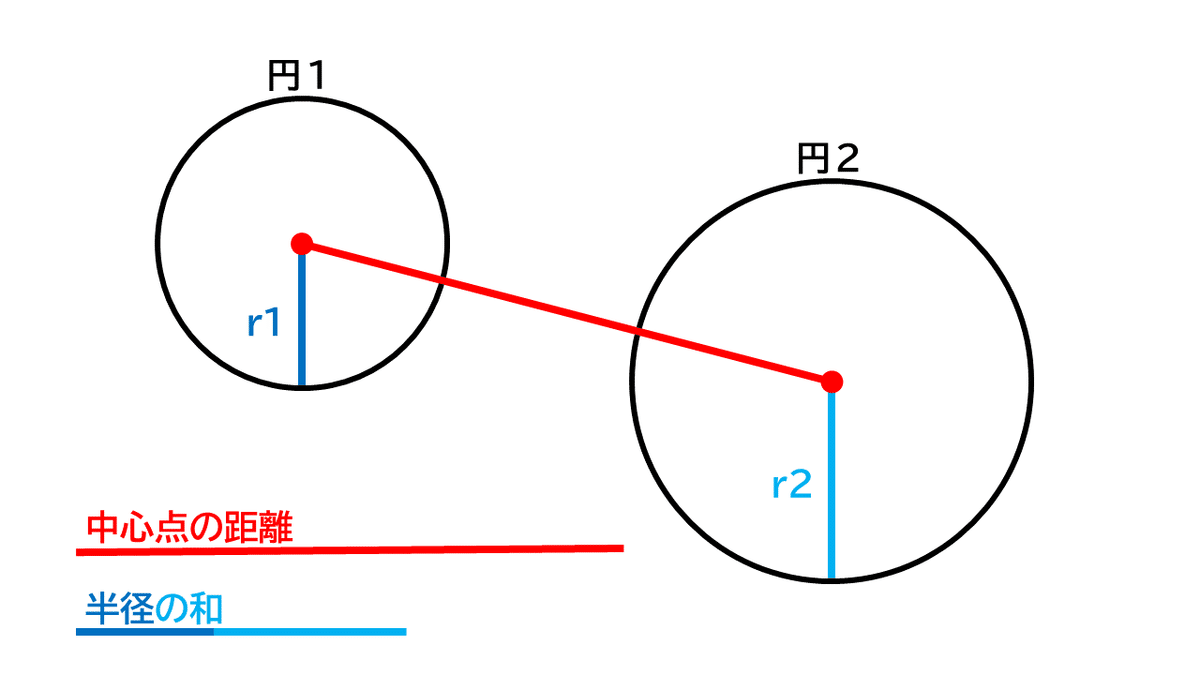
2つの円の「中心点の距離」と「半径の和」を比べて、半径の和のほうが大きければ当たっているといえます。

例えば、このように円があった場合

中心点の距離は、円１と円２の中心点をまっすぐつないだ線の長さ、

半径の和は、円１と円２の半径を足した線の長さとなります。

そして、二つの線の長さを比べて、

中心点の距離が半径の和より大きければ、二つの円は当たっていない、

中心点の距離のほうが長い

中心点の距離より半径の和のほうが大きければ、二つの円は当たっているということになります。

半径の和のほうが長い

計算方法

中心点の距離を求めるには、中学校で習った三平方の定理というものを使います。

直角三角形の斜辺の部分が、今回求めたい「中心点の距離」です。

まずは、二つの円のｘ同士とｙ同士の引き算をしていきます。
今欲しい情報はａとｂの長さなので、１と２の順番を変えても結果は変わりません。

aとbの長さを求める

ａとｂの長さがわかったらｃの長さを求めます。

半径の和は、二つの円の半径を足し合わせるだけでいいので簡単ですね。

あとは、中心点の距離と半径の和の大きさを比べて、中心点の距離のほうが小さければ当たっている。そうでなければ当たっていないと判定できます。

サンプル

c++でのサンプルコードです。

#include <math.h>

/*計算に必要な情報*/
//円１の中心座標
float circle1X;
float circle1Y;
//円１の半径
float circle1R;

//円２の中心座標
float circle2X;
float circle2Y;
//円２の半径
float circle2R;


/*当たり判定の計算*/
//中心点の距離
float lengthX = circle1X - circle2X;
float lengthY = circle1Y - circle2Y;
float centerDistance = sqrtf(lengthX * lengthX + lengthY * lengthY);

//半径の和
float radiusSum = circle1R + circle2R;

//中心点の距離より半径の和のほうが大きい
if (centerDistance <= sumRadius)
{
	//二つの円が当たっている
	return true;
}

//二つの円が当たっていない
return false;