NBA新人選手の5年後在籍予測について
NBAに入った新人選手が5年後も在籍しているのかどうか、彼らの詳細データを説明変数として、在籍有無を予測するモデルを作成する。
データセットはKaggleより借用:下記
5 Year Survival of NBA Rookies from 1980-2015
https://www.kaggle.com/datasets/mamadoudiallo/5-year-survival-of-nba-rookies-from-19802015?resource=download
ExcelファイルのGoogleドライブのURL(上記からダウンロードしたもの)
https://drive.google.com/file/d/1x5M3k8GxuYDBcBIaTiS1VR3nFR3CU0ws/view?usp=sharing
■ ライブラリのインポート
#基礎
import pandas as pd #1
import seaborn as sns #2
import matplotlib.pyplot as plt #3
import numpy as np #4
#XGboost
from xgboost import XGBClassifier
from sklearn.metrics import accuracy_score
#Logistic
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
#PCA
from sklearn.decomposition import PCA※ライブラリのバージョン確認
pip show pandas
pip show seaborn
pip show matplotlib
pip show numpy
pip show xgboost
pip show sklearnName: pandas = Version: 1.3.5
Name: seaborn = Version: 0.11.2
Name: matplotlib = Version: 3.2.2
Name: numpy = Version: 1.21.5
Name: xgboost = Version: 0.90
Name: sklearn = Version: 0.0
■ データの読み込みと確認
20個の説明変数と、1つの「target」である目的変数が確認できる。
説明変数の解釈については、追って述べることとする。
また、データ内に欠損値はないことも確認できた。
#データを読み込み名前を付ける
df = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/rookie_df.csv")
df.head()
df.info()
■ 説明変数の解釈を整理
一つ一つの意味を理解しながら、自分なりの仮説もイメージする
Year Drafted : (NBA加入年)
GP: games played during rookie season(ゲーム出場数)
MIN: average minutes played per game(試合当たりプレイ時間)
PTS: average points per game(平均得点数)
FGM: average field goals made per game (試合当たりの得点数)
FGA: average field goals attempted per game (試合当たりのシュート数)
FG%: average field goal percentage (試合当たりのゴール成功率)
3P Made: average 3-point field goals made per game(試合当たり3ポイント得点数)
3PA: average 3-point field goals attempted per game(試合当たり3ポイントシュート数)
3P%: 3-point percentage(3ポイント成功率)
FTM: average free throws made per game(試合当たりフリースロー得点数)
FTA: average free throws attempted per game(試合当たりフリースローシュート数)
FT%: free throw percentage(フリースロー成功率)
OREB: average offensive rebounds per game(オフェンスリバウンド数)
DREB: average defensive rebound per game(ディフェンスリバウンド数)
REB: average total rebounds per game(平均リバウンド数)
AST: average assists per game(平均アシスト数)
BLK: average blocks per game(平均ブロック数)
TOV: average turnovers per game(平均ターンオーバー数)
EFF: a player's efficiency; EFF = (PTS + REB + AST + STL + BLK - Missed FG − Missed FT - TO) / GP(プレーヤーの効率性)
■ 説明変数を統計量から理解を深める
各項目の統計量を確認し、全体のデータ感を掴む。
項目によっては数値に振れ幅があるので、標準化をする必要がありそうだ。
#一覧で値を確認
df.describe()
■ モデル化前のデータ整備
「target」変数を除いたものを説明変数 X とし、yを「target」の目的変数とする。併せて、テストデータとして25%を確保し、標準化もする。
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
X = df.drop('target', axis=1)
y = df['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
ss = StandardScaler()
X_train_scaled = ss.fit_transform(X_train)
X_test_scaled = ss.transform(X_test)■ XGboost
Kaggleで今もっともアツい機械学習モデルと噂されるXGboostを使用する。
XGBoostは、複数の決定木を組み合わせて学習することで高い精度を実現していると言われている。
from xgboost import XGBClassifier
model_XGBS = XGBClassifier()
model_XGBS.fit(X_train_scaled, y_train)
importances = pd.DataFrame(data={
'Attribute': X_train.columns,
'Importance': model.feature_importances_
})
importances = importances.sort_values(by='Importance', ascending=False)y_pred_XGBC = model_XGBS.predict(X_test_scaled)
print('Accuracy:',accuracy_score(y_test,y_pred_XGBC))Accuracy: 0.6769662921348315
約68%の当てはまりの良さが出た。
念のため、学習データでの精度も確認する。
Accuracy: 0.848314606741573(約85%)
学習でーたでは相対的に優秀な精度を出していることがわかる
y_pred_XGBC_train = model_XGBS.predict(X_train_scaled)
print('Accuracy:',accuracy_score(y_train,y_pred_XGBC_train))■重要な特徴量の確認
得たモデルにおける各特徴量の重要度を表したグラフを図示する。
特に重要度が大きい上位3つの特徴量はそれぞれ「PTS : 平均得点数」「EFF : プレーヤーの効率性」「MIN : ゲーム出場数」を示している。どうやら在籍の判定には、バランス良く平均的に得点をし多くゲームに出場することが重要だと言える。
plt.bar(x=importances['Attribute'], height=importances['Importance'], color='#087E8B')
plt.title('Feature importances obtained from coefficients', size=20)
plt.xticks(rotation='vertical')
plt.show()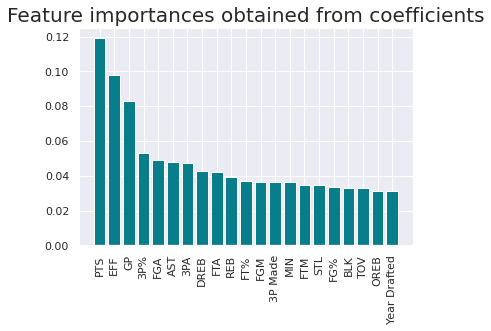
■ LogisticRegression
XGBoostだけでなく、ロジスティック回帰分析も試してみる。ロジスティック回帰分析は、いくつかの要因(説明変数)から「2値の結果(目的変数)」が起こる確率を説明・予測することができる統計手法となり、今回のようなケースには活用できると考える。
from sklearn.linear_model import LogisticRegression
model_logi = LogisticRegression()
model_logi.fit(X_train_scaled, y_train)
importances = pd.DataFrame(data={
'Attribute': X_train.columns,
'Importance': model.coef_[0]
})
importances = importances.sort_values(by='Importance', ascending=False)y_predlogi = model_logi.predict(X_test_scaled)
from sklearn.metrics import accuracy_score
print('Accuracy:',accuracy_score(y_test,y_predlogi))Accuracy: 0.7162921348314607
約72%の当てはまりの良さが出た。
念のため、学習データでの精度も確認する。
Accuracy: 0.6956928838951311(約70%)
y_predlogi_train = model_logi.predict(X_train_scaled)
print('Accuracy:',accuracy_score(y_train,y_predlogi_train))■重要な特徴量の確認
得たモデルにおける各特徴量の重要度を表したグラフを図示する。
特にプラスの重要度が大きい上位3つの特徴量はそれぞれ「GP : ゲーム出場数」「FTM : 試合当たりフリースロー得点数」「DREB : ディフェンスリバウンド数」を示している。ロジスティック回帰分析だと、在籍の判定には、ディフェンスリバウンドを取り、フリースローを决め、ゲームに出場することが重要だと言える。
こちらの方が、当てはまりは高いが、バスケットボールのゲームの中での解釈としては少し不自然にも感じる。
plt.bar(x=importances['Attribute'], height=importances['Importance'], color='#087E8B')
plt.title('Feature importances obtained from coefficients', size=20)
plt.xticks(rotation='vertical')
plt.show()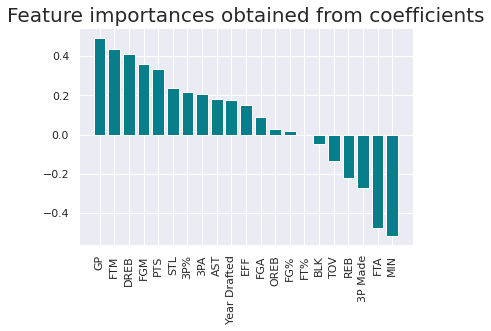
■ 課題と検討
Accuracyの確度を向上させる施策として、クロスバリエーションや、今回時間の都合で全て出来なかったがPCA(主成分分析)で次元圧縮し新しい少数の成分でモデル化するなども検討の余地は残る。またロジスティック回帰分析ではオッズ比が重要となるため、その点の検討があった方がより意義のあるブログになったかもしれない。
■ 追加:主成分分析(PCA)
「target」の0/1を判別するには説明変数が多すぎるという側面もあった。従って、説明変数を削減するため主成分を見てみる。
from sklearn.decomposition import PCA
pca = PCA().fit(X_train_scaled)
plt.plot(pca.explained_variance_ratio_.cumsum(), lw=3, color='#087E8B')
plt.title('Cumulative explained variance by number of principal components', size=20)
plt.show()
5つ程度の主成分で90%のデータを説明できていることがわかる。また、2.5個で80%のデータを説明できていることがわかる。以降は、分析者の勘所で决めて良いと考える。
loadings = pd.DataFrame( data=pca.components_.T * np.sqrt(pca.explained_variance_), columns=[f'PC{i}' for i in range(1, len(X_train.columns) + 1)], index=X_train.columns)loadings.head()
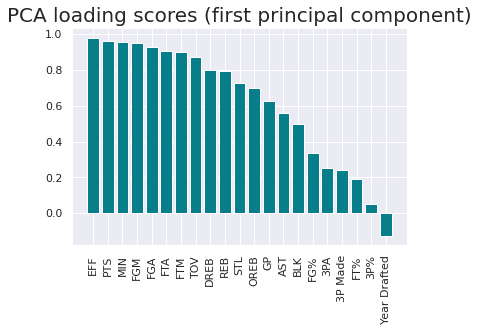
PC1のloadingsを確認してみると、下記のような図示となる。
ここから成分の名前を分析者のセンスで決めていく形となる。成分1は平均的な力が求められることから「バランス力」とでも定義し、スコアを変数として扱い、改めて同様のモデルに突っ込むことも解釈容易性を緩和させる施策となり得ると考える。
pc1_loadings = loadings.sort_values(by='PC1', ascending=False)[['PC1']]
pc1_loadings = pc1_loadings.reset_index()
pc1_loadings.columns = ['Attribute', 'CorrelationWithPC1']
plt.bar(x=pc1_loadings['Attribute'], height=pc1_loadings['CorrelationWithPC1'], color='#087E8B')
plt.title('PCA loading scores (first principal component)', size=20)
plt.xticks(rotation='vertical')
plt.show()