
内角和が180°以外の三角はコレですか? NHK「笑わない数学 ユークリッド幾何学」を観て
第2シリーズ 非ユークリッド幾何学 - 笑わない数学 - NHK

NHKの笑わない数学2
ユークリッド幾何学 を観て
数学素人の自分は解った様な
解らない様な感じなんですが
数式や論理は言葉を尽くされても
良く分かりませんが
番組内で放送していた
「ユークリッド幾何学では三角形の内角の和が180°以外はあり得ない」とか
「非ユークリッド幾何学ではあり得る」とか言うのを見ていて
●三角形の辺が直線だと180°以外はあり得ないけど
曲線ならあり得るよな。
と思ったのですが、、、
✖不可「直線三角形」
◎ 可「曲線三角形」

こういう事ですか?
三角形の定義には直線か曲線かは明記されていないのです
例えば三角の生地で球形ボールを作ろうと思えば
直線三角では隙間が開いて作れないので
3辺共に膨らんだ生地を貼り合わせる事になる
その角は60°では収まらないから
60°以上の70°とかに膨らむはず
上記の【黄緑三角】で見れば外線の三角は辺が外側に膨らんでいるので
その内角和は180°を超えた、例えば210°とかになりますよね?
内線の【白三角】は3辺共に内側にたわんでいるので
180°以下の150°とかになりますよね?
180°以上だと、おにぎり🍙みたいです

地球やボールやおにぎりは
昔から存在していますし
三角地帯の道路なんかも
直線とは限りませんよね

この三角地帯の右下の角は
60°以下ですよね
つまり内角和が180°以外の三角は
現実に存在を昔からしている
と言う事なんじゃないですかね?

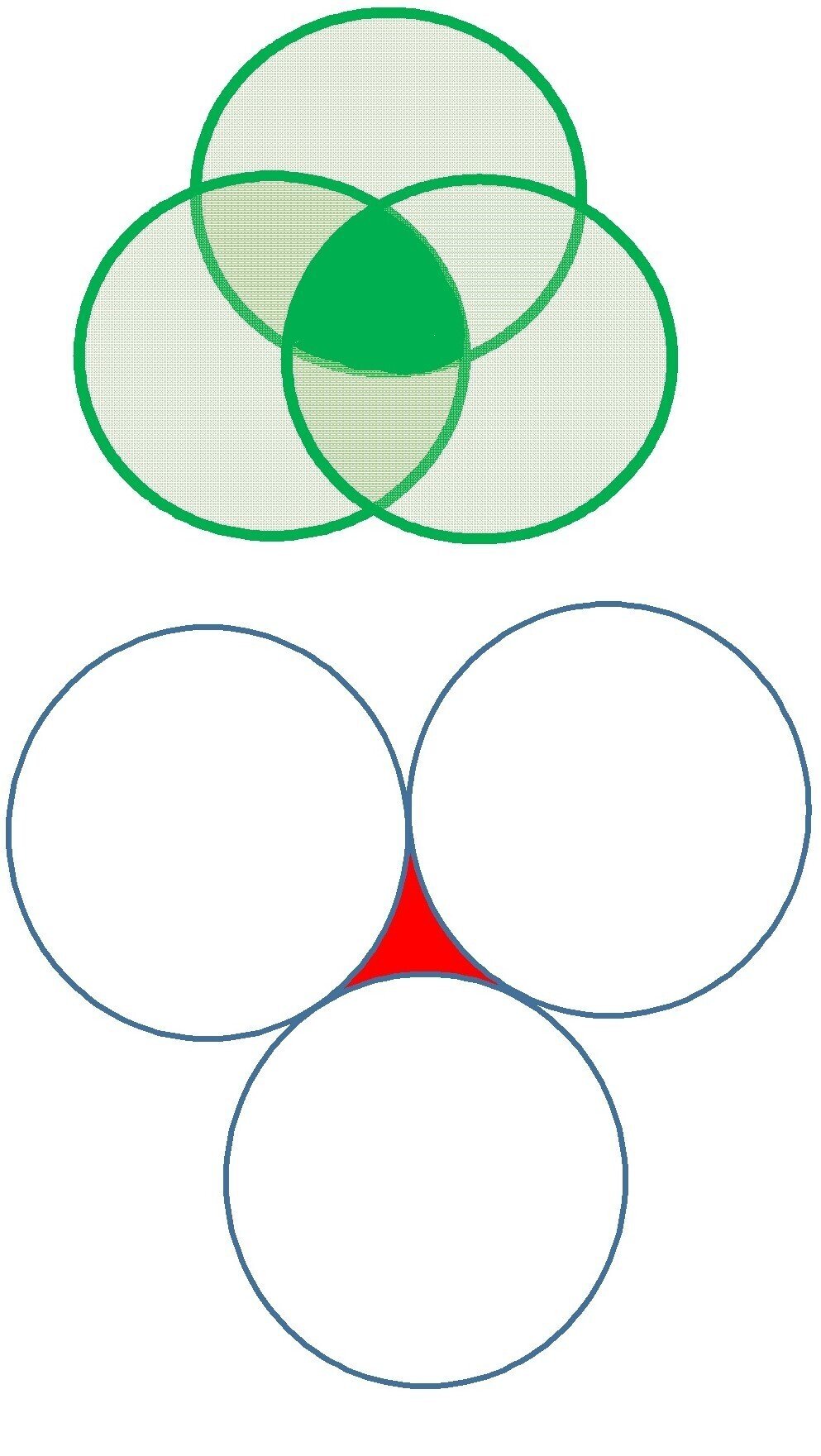
直線以外の曲線でなら現実社会に
非ユークリッド幾何学は既に存在してた
以上です
