金融時系列における機械学習のオーバーフィット対策
botter_01です。
本記事はマケデコAdvent Calendar 2024の記事として執筆させていただきました。
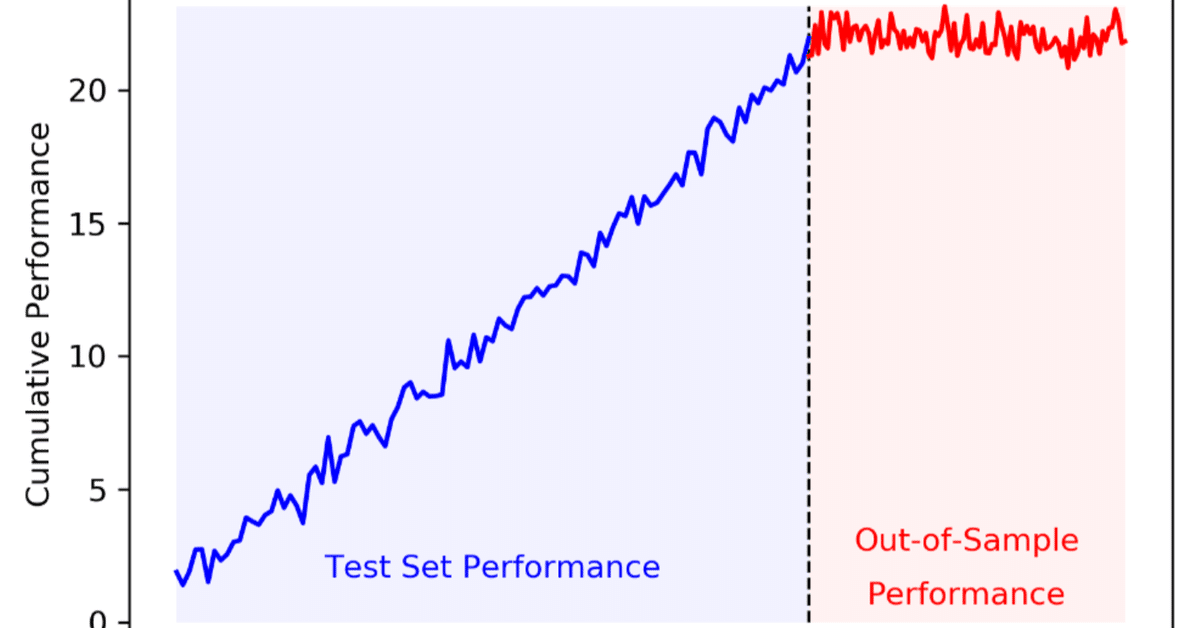
早速ですが,皆様は下記のような損益曲線を見たことがありますでしょうか。
株や仮想通貨の時系列データの予測に対してlightGBM等の機械学習を適用したり,TradingView上でバックテスト結果を見ながらパラメータの最適化すると青い損益曲線が得られ,ウキウキで戦略を実行したのも束の間,赤の損益曲線のようなヨコヨコ,もっと酷い場合は手数料負けによって安定した損失を生み出し続ける戦略になってしまった…そんな経験はありませんか?(私は死ぬほどあります)
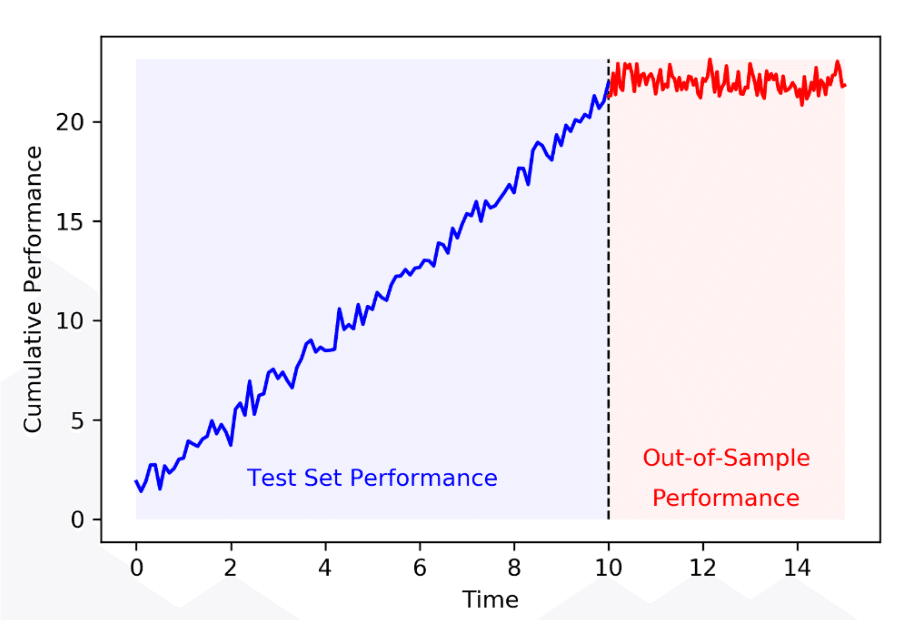
この現象は,最適化手法,特に機械学習において問題となる「オーバーフィット」と呼ばれるものです。
本記事では、株や仮想通貨等の金融時系列データにおける機械学習モデルが陥りがちなオーバーフィットにフォーカスし、その原因や防止策の実例を紹介していきます。
機械学習の予測における誤差の分解
まず初めに,金融時系列に対するオーバーフィットを考えるために機械学習の予測問題で生じる誤差を分解して考えます。
いま,目的関数$${y}$$を予測する$${f[x]}$$を考えます。
このとき予測不可能なノイズが
$${\epsilon = y - f[x]}$$
であり,この$${\epsilon}$$は$${\epsilon \text{\textasciitilde}N[0,\sigma_E^2]}$$です。
また,モデルは$${f[x]}$$を近似する関数$${\hat{f}[x]}$$を探します。
予測問題として,
$${y}$$と$${f[x]}$$の二乗誤差(MSE:Mean Squared Error)の期待値$${E[(y-\hat{f}[x])^2]}$$を最小化することを考えます。
このMSEは下記のように分解できます。

バイアス:予測すべき目的関数とモデルの予測値(の期待値)の差
バリアンス:モデルの予測値の分散
ノイズ:予測不可能なランダム要因
バイアスとバリアンスの模式図は下図が分かりやすいです。
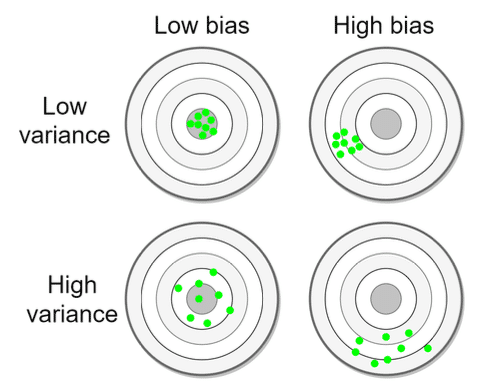
バイアスは訓練データにアンダーフィットすることで発生します。すなわち予測モデルがシグナルをノイズだと勘違いしてしまうことで生じます。
バリアンスは予測モデルがオーバーフィットすることで発生します。すなわち予測モデルがノイズをシグナルだと勘違いしてしまうことで生じます。
ここで,上述の通りノイズは予測不可能であるため,予測問題を解く(MSEを最小化する)ためにはバイアスとバリアンスを低減することが求められます。その際,一般的にバイアスとバリアンスはトレードオフの関係にあると言われています。
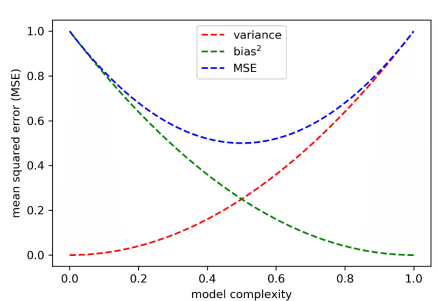
上記によれば,横軸のモデルの複雑さ(model complexity)が上がるにつれてバリアンスが大きくなっていくことが分かります。これは機械学習モデルが複雑であるが故にモデルが本来予測不可能なノイズεまで予測しようとすることで生じます。
機械学習は訓練データに信号が存在しなかったとしてもノイズから何かしらのパターンを見つけてしまいます。
このように機械学習モデルのオーバーフィッティングは,モデルの複雑さ故,高いバリアンスによってもたらされます。
2種類のオーバーフィッティング
一般的に機械学習においてはデータセットを以下の通り2分割します。
訓練データ(validationデータ含む)
テストデータ
これから訓練データ,テストデータのそれぞれにおけるオーバーフィッティングの原因とその対策を記載します。
訓練データのオーバーフィッティング
原因:モデルの複雑さ
前述した通り予測モデルが複雑すぎると,信号ではなくノイズまで予測するモデルになってしまいます。

例として,黒の点で表される観測データを予測するモデルとしては黒の実線が汎化性能の優れた予測値と考えられますが,複雑すぎるモデルは青い曲線として予測値を出力してしまいます。
これではモデルの汎化性能が悪いことは容易に予想できます。
訓練データにおけるオーバーフィットはモデルの複雑さに起因します。そこで,以下に対策としてモデルの複雑さを下げる方法を記載していきます。
対策①:モデルをシンプルにする
オッカムの剃刀「ある事柄を説明するためには,必要以上に多くを仮定するべきでない」や赤池情報量規準(AIC)の考え方等にも示されるとおり,モデルの自由度を必要以上に増やすことは避けるべきです。
筆者が実践している例としては,過去記事のコード部分からも分かりますが,lightGBMにおけるmax_depthを3~6程度の低めの値に設定する等,ハイパーパラメータの自由度を低く設定しています。
対策②:データの拡充
十分な長さのヒストリカルデータを入手するなどして,できるだけ独立な訓練データの数を増やす必要があります。独立と記載したのは,日足戦略を策定する際に,0:00〜23:59のリターンと同日0:01〜24:00のリターンを別なサンプルとして学習することは冗長性の観点からあまり意味がないことを指しています。
したがって,同期間のヒストリカルデータしか得られない場合は長時間足の戦略になる程,必然的にデータ数が減るため注意が必要です。
また,ラベルの正例のバランスにも考慮する必要があります。
訓練データ全体で正例が数回しか発生しないものに対して複数のパラメータを最適化することは自由度が不足し,オーバーフィットの原因となります。
例えば、ある価格時系列のX日移動平均に対して終値がY%下がったら買いといった戦略の最適化を考える際,買いの例(正例)のサンプル数が訓練データに対して少ないことが予想され,簡単にオーバーフィットしてしまいます。
対策の実例として,少数例のラベルの重みづけをする方法等があります。
気になる方は「不均衡データの対処法は?」等とLLMに尋ねることでたくさんの回答が得られると思います。
対策③:アンサンブル
アンサンブル手法は,相関の低い弱学習器を組み合わせて使う(例えば平均を取る)ことでパフォーマンスの向上を目指すものです。
アンサンブル手法の例として次のものが挙げられます。
Bagging (Bootstrap aggregating)
Boosting
この中でも特にBaggingはバリアンスを低減する効果があるとされ,金融時系列には特に有効な手法です。
一方でBoostingはバイアスの低減に対してより有効な手法で,lightGBMのアルゴリズムにも組み込まれています。
Baggingの手法については,次のように解説されています。
この手法は次のように機能する。最初に,復元抽出を伴う無作為抽出によりN個の訓練データセットを生成する。次に,各訓練データセットにつき1つずつ,N個の推定器を訓練する。これらの推定器は互いに独立に訓練することになるため,モデルは並列に推定することが可能である。最後に,アンサンブル予測をN個のモデルによる個々の予測の単純平均で求める。
上記の考えにしたがって,CVにおいてfoldごとに学習し,それら予測値の平均を最終的な予測値とすることなども考えられると思います。
また,kaggle等でよく使われるrandom seed averagingもアンサンブル手法の一つです。(下記記事ではもはや常識と記載されていますね)
対策④:正則化
正則化はモデルの複雑さにペナルティを与える手法です。
線形回帰では下記の手法が有名です。
LASSO : L1正則化
Ridge : L2正則化
Elastic Net : L1+L2正則化
これらはscikit-learnの関数として実装されているため,簡単に使用できます。
lightGBMでもハイパーパラメータとしてL1・L2正則化を指定できますし,深層学習においてもdropout等による正則化が用いられることがあります。
対策⑤:汎化誤差の計測(テストデータ)
訓練時に,テストデータに対する汎化誤差を計測することで,オーバーフィットした予測モデルを棄却することができます。汎化誤差を精度良く推定するための手法としてリサンプリングが挙げられます。
一般的には,時系列データをある割合で訓練データとテストデータに分割し,より直近の時系列データをテストデータにします。(train_test_splitにおいてshuffle=False)
一方,この分割法で得られたテストデータは単に実現したランダム経路の1つに過ぎず,実運用時のout-of-sample(OOS)データとは異なる可能性があります。
そこで,テストデータをリサンプリングをすることで複数シナリオのテストデータを取得します。多数のシナリオに対して汎化誤差(の分布)を計測することでオーバーフィットの確率を下げることが期待できます。
具体的には,
K-fold CV, CPCV
Random Sampling(例:bootstrap法)
などが挙げられます。
上記の方法でリサンプリングすることで,ウォークフォワードテストとは異なり,時系列的な関係が崩れますが複数の系列を得ることができます。重要なのは,ヒストリカルに正確なパフォーマンスを得ることではなく,複数シナリオをシミュレーションすることです。
SIGNATEのファンダメンタルズ分析チャレンジにおいて1位を獲得した望月さんもCVを用いていたようです。
なお,CPCVについては「テストデータのオーバーフィッティング」の「対策②」で後述します。
テストデータのオーバーフィッティング
続いてテストデータのオーバーフィッティングについて,その原因と対策を記載します。
原因:複数回テストによる選択
テストデータに対するオーバーフィッティングは「複数回テストによる選択バイアス」(SBuMT:Selection Bias under Multiple Testing)により生じます。
伝統的な統計学はコンピュータが発明される前に体系化されたものであり,テストは一度しか行われていませんでした。現在でも使われているp-値検定は複数回テストを行うことを想定しておらず,複数回テストによる選択バイアス(SBuMT:Selection Bias under Multiple Testing)が問題となります。
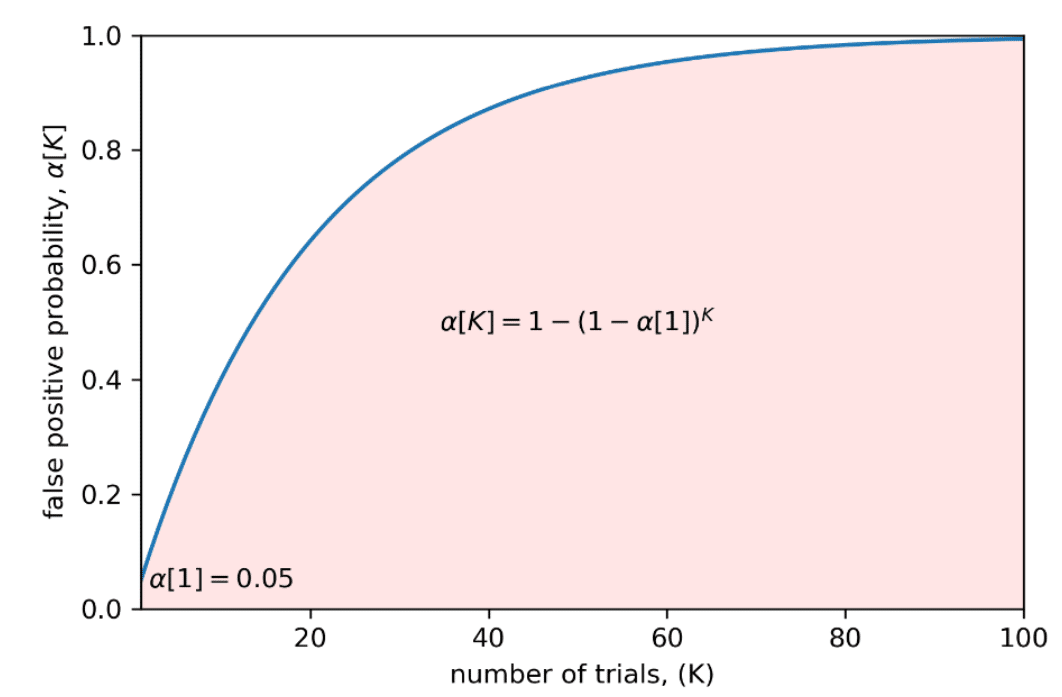
上の図の例では,各独立なテストは5%の偽陽性率(α[1]=0.05)を持つため,複数回テストを行うことで偽陽性率はすぐに大きくなってしまいます。
偽陽性(False Positive)とは,本来は陰性であるのに,誤って陽性と判定されること。
今回の例では,本来はout-of-sample(OOS)データに対して汎化性能がないものを誤って汎化性能があると判定してしまうこと。
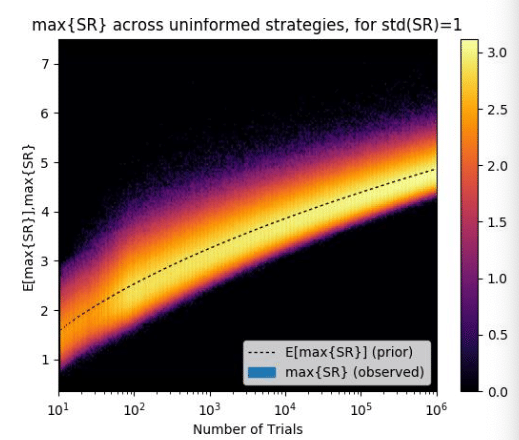
次の図はテスト回数とシャープレシオの関係です。
横軸の試行回数が増えるごとに最大シャープレシオの期待値(点線)が上昇していくことがわかります。この例での実際のシャープレシオの期待値は0です。1000回の試行時点では最大シャープレシオの期待値は約3にも及びます。
なお,試行ごとのシャープレシオの分散が高いほど,すぐに最大シャープレシオの期待値は上昇してしまいます。(例えば,複数戦略を用意したとき,これら戦略のパフォーマンスの分散が高い場合,それらのシャープレシオの最大値が高くなりやすいことが想像できると思います。)
最適化時のノウハウでよく知られた話として「グリッドサーチによってパラメータを最適化して戦略のパフォーマンスを測るとき,パラメータを少し動かしただけでパフォーマンスが激しく上下する(プロフィットスパイク)戦略は避け,パラメータに対してパフォーマンスが安定している戦略を選ぶべき」とされるのは上記の図からも説明可能です。
このようにテストデータはSBuMTによりバックテストを複数回実行することで簡単にオーバーフィットしてしまうことが分かります。
以下に対策を記載していきます。
対策①:試行回数を調整する
メンタル的に中々難しいのですが,テストデータのバックテストは1回きり,駄目だった時点でそのモデルは棄却し,別戦略を作り直す心持ちが必要です。
バックテスト結果を見てパラメータを調整した時点でそのテストデータはテストデータではなくなるのです。
なお,ファイナンス機械学習ではこの問題に対処するため,デフレシャープレシオが紹介されています。数式は本書に記載があるため割愛しますが,バックテスト回数によってシャープレシオを割り引くという考え方です。
デフレシャープレシオを使わないにしても試行回数を増やすにつれて,バックテスト結果から出力されたシャープレシオの蓋然性は低下していることに気をつける必要があります。
辛抱強く試行を重ねるbotterの皆様の勤勉さが仇になるということです😇
対策②:汎化誤差の計測(OOS)
今回はテストデータからも切り離されたOOSデータを用いて汎化誤差を測定します。
訓練データのオーバーフィッティングの対策⑤で述べたリサンプリング手法をOOSに対して適用することが同様に対策となります。
ここでは,リサンプリング手法のうち前述したCPCV(Combinatorial Purged Cross Validation)について詳しく記載されている記事を紹介いたします。
下図の通り,通常のCVではバックテスト経路(赤線)は1種類しか得られないのに対して,CPCVではバックテスト経路を複数得ることが可能です。

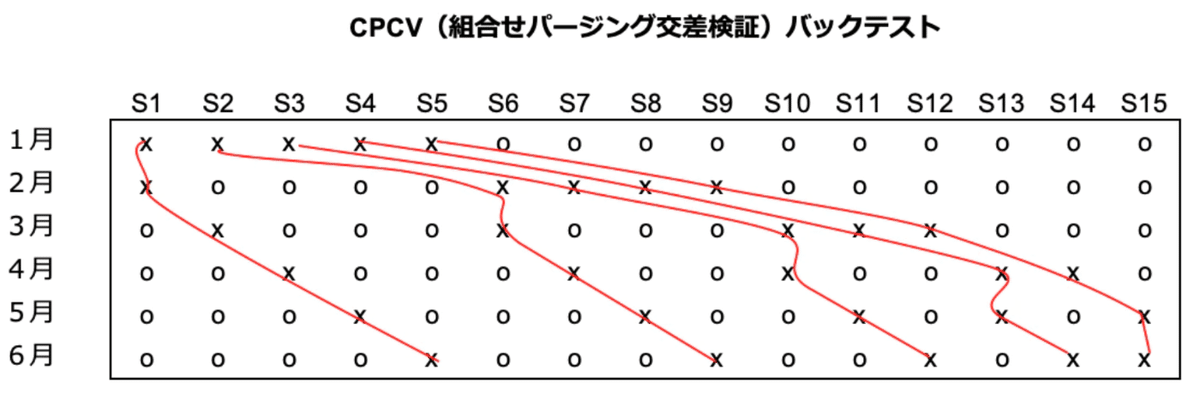
CPCVにより,バックテスト経路が複数得られ,その結果パフォーマンスの分散が小さくなることになります。(理論的な証明は前述の記事をご参照ください。)
試行ごとのシャープレシオの分散が高いほどすぐに最大シャープレシオの期待値は上昇してしまうことを先に述べましたが,CPCVでの評価によりパフォーマンスの分散が小さくなります。その結果,下図(再掲)のシャープレシオが上がりにくく,すなわち本来のシャープレシオとして評価できる確率が高くなります(=偽陽性率を下げることが出来る)。

まとめ
本記事では、金融時系列の機械学習において問題となるオーバーフィットについて、訓練データとテストデータそれぞれの観点からその原因と具体的な対策を紹介しました。SNの低い金融時系列予測であっても、モデルの単純化、データ拡充、アンサンブル、正則化、そしてリサンプリング手法による汎化誤差の精緻な評価など、オーバーフィット対策には様々なアプローチがあります。
(それでも対処出来るとは言ってない)
皆さまの爆散防止にお力添え出来ますと幸いです。
参考にした書籍(と格言)
バックテストの目的は悪いモデルを切り捨てることであり,それを改善することではない。
もはや今更感のある名著。本記事の内容の大部分がファイナンス機械学習にて議論され、著者がレクチャーとしてまとめている内容です。機械学習で金融時系列を予測したい方は必ず読むべき内容だと思います。
われわれが探しているのは最適な手法ではなく,確実な手法である。
機械学習まで使わずとも,ルールベースやトレビューのバックテスト機能等で戦略を構築される方はこちらの方がおすすめです。記事の途中で説明したプロフィットスパイクを始め、最適化の注意事項について詳しい記載があります。
仮想通貨界隈へ機械学習の大流行をもたらしたrichmanbtc先生の著書。これから仮想通貨で爆益を得たい!という方々に読み物的におすすめです。