計量経済学 OLSの仮定と性質について
If you need to explain what is the econometrics in 3 min, you should split almost time to talk about the assumptions and violation. (もし3分で計量経済学を説明するなら、仮定とその侵害について話すべきです)
初回の計量経済学の授業では、先生にこんなことを言われました。つまり、仮定がどんなときに発生し、どんな時に侵害されるかが計量経済学においては最も大切ということです。
ここは専門用語が多くて英語だと躓きやすいと思います。
(References: RWTH Aachen "microeconometrics" Sose2020, Almut Balleer, Chair for applied economics)
OLSでの3つの仮定
OLSをするにあたっておく仮定は3つあります。
OLS1.Exogeneity 外生性
E(u|x)=0
The error terms is unrelated to explanatory variables.
OLS2. No perfect multicollinearity 多重共線性がない
rank(X'X)=k where X = x1...k
OLS3. Homoscedasticity 等分散性
Variance of u does not vary with explanatory variables.
OLSが満たす3つの性質(BLUE)
OLSは上記の3つの仮定をみたすときに、以下の3つの性質を持ち、best linear unbiased estimator(BLUE)( ベストなバイアスのない線形回帰分析)といわれる(Gauss Markov Theorem)
i. Consistency
ii. Unbiasness
iii. Efficiency
仮定の解説
まず仮定の方から。3つありますが、2つについては、すでに前に話したOLSの計算の際に用いているものです。それは1つめのExogeneityと、2つめのrankについてです。3つ目のHomoscedasticity等分散性については、計算のためではなく、今後のモデル評価のため(std. error, t-value)に必要なものになります。
OLS1.Exogeneity
Def:
1.Exogeneity 外生性
E(u|x)=0
The error terms is unrelated to explanatory variables.
このE(u|x)=0というのは、もともとサンプルがiid、つまり適当にランダムにとってきたという仮定に基づいており、OLSにおいてβを計算するのに必要なものでした。
日本の教科書ではこのExogeneityではなくiidの条件を仮定として書いているものもありましたが、Exogeneityが満たされている⇒iidも満たされているといえるので、どちらでもいいということなのでしょう。
この条件は、error termsが説明変数と関係がないともいえるので、そう書くことも多いです。
Effect:
一人だと弱いけど、友達のrank君と一緒なら頑張れる、みたいな子です。
まず、これとrankの条件がそろうと、OLSが計算できます。これを、
β is identified.
といいます。
次に、rank君と一緒で、かつデータがたくさんあれば、推定した値β_hatと本当のβは大体同じだろう、といえます。これを、
β_hat is consistant for β. (一致性)
といいます。式で書くとこう。

Nはサンプル数で、ε(イプシロン)はめっちゃ小さい適当な数。頭に^(ハット)がついているのはβ_hat。
サンプルNがすごく大きいと、推定したβと本当のβの差がちょびっとでも違う確率はゼロに近づいていく。
という意味です。
これによって、推定者は初めて推定した値βを、本当のβの代わりとして、信用することができます。
また、rank君と一緒だと、これも成り立ちます。
OLS is unbiased conditional on X.(不偏性)
Xについてのバイアスがない、というのは推定が母集団における本当の値を正しく推定できている、という意味。数式だとこう。
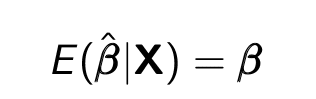
Bias は、ここから
Bias = E(bata_hat|x) - bata
で求められます。
これらの違いとしては、一致性というのはNが大きくなればβに近づくので、Nが大きいことが条件だが、不偏性はそうではないこと。逆に言えば、Nがいくら大きくても、バイアスは消えないということ。
例えば、ある地区の投票結果の予測をいくらかのサンプルからしたいとき、もしランダムに取り出せばいい普遍性をもった予測ができますし、たくさんNがあれば、その結果はだんだん本当の値に近づきます。しかし、もし固定電話でそのサンプルを取得したとすると、固定電話を持っている人は限られ、そのサンプルにも偏りが出る(お金がある人、若い人は少ないなど)のでいくらそのNを大きくしてもそのβは信用できないとなります。
実際には、サンプルが本当にランダムであるとはデータをパッとみてもわからないので、逆に上記の仮定exogeneity やrankの仮定が満たされているかを確かめることで、間接的に一致性、不偏性を得ることで、サンプリングがiidであるとわかるのです。
OLS2. No perfect multicollinearity
def:
2. No perfect multicollinearity 多重共線性がない
rank (X)=k where X = x1...k
X is of full rank.
これも前回の計算の際に使った、Xが正則行列であることの仮定の変形です。Xが正則行列なら、可逆行列なので、βを求めることができたのでした。
多重共線性がないというのは、簡単いうとおんなじような変数が2つ以上入っていないという意味です。ある変数(群)で別の変数を表すことができる場合、多重共線性があるといいます。
例えば、変数の中にsalesと、sales*2という二つの変数がある場合、rankX=k-1となってしまうので、多重共線性があるといえます。
他にも、sales, profit, costという変数があれば、profit = sales - costで求められるので、rankはフルでなくなり、多重共線性があるとなります。
また、ダミー変数の罠というものがあり、男=1、女=0のように仮に数字をおいて変数を作る作業(ダミー変数)をしたときにも、もし男と女を両方含めると、women = -men として算出できてしまうので、ダメです。年とかも、1999-2002までの年のダミーがある場合、もし1999=0, 2000=0, 2001=0なら2002=1だと推定できるので、2002を除いてあげないと多重共線性があるとなってしまいます。
Effect: これは上記で書いたexogeneityとのコラボで生まれる、一致性と不偏性です。
OLS3.Homoscedasticity 等分散性
Def:
3. Homoscedasticity 等分散性
Variance of u does not vary with explanatory variables.
かっこいい感じですね、名前。
errorの分散とXの関係性がないとき、等分散性homoscedasticityが満たされているといいます。
逆に、もしxによってerror termの分散が異なる場合、上記は満たされず、heteroscedasticityである、といいます。
例えば、男女の変数があり給与との関係を知りたいとき、男女で給与の分散は違うと思います。(おそらく女性は給与=0が多く、男の方が大きい)この時、homoscedasticityが満たされない可能性があるでしょう。
数式で書くとこう。
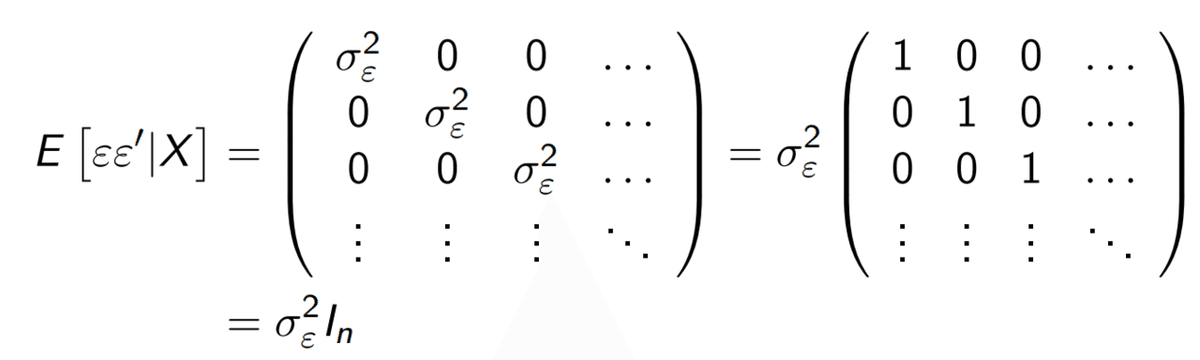
ε(イプシロン)はerror term(uだったもの)。これは、
the variance of error term is a constant , and no correlation between error term. (エラーの分散(斜めの場所)は一定の値で、エラー同士の共分散は0。)
という意味です。この時
The error term is homoscedastic and not correlated
とかって言います。
とりあえずは最初のdefに書いた、errorの分散とXの関係性がない、という点を覚えておけば大丈夫です。
Effect:
The estimator become efficient.
If vaolated, std error & t stat has no meaning.
このhomoskedasticityが満たされていると、推定は効率的になる、といいます。ここでの効率的というのは、ある推定の分散がより小さいという意味。誤差項error termがheteroskedasticであることは、その推定の分散が小さいことがしめされています。
そして分析の際に重要なことが、標準誤差(std error)とt値(t value)が正しくなくなってしまうことです。分散が正しくないので、それをもとに計算する標準誤差、また標準誤差をもとに計算するt値も影響を受け、結果が変わってしまいます。
t値が変わるということは、分析で大切な有意性significanceに意味がなくなるということ。よって、もし共変量coefだけに興味があるなら、仮定1,2だけでいいですが、その有意性を示す場合はこの仮定3が必要です。
BLUE
If OLS1-3 hold, OLS become best unbiased estimator.
もし仮定1-3がすべて満たされたとき、OLSはbest linear unbiased estimator(BLUE)( ベストなバイアスのない線形回帰分析)といわれます。(Gauss Markov Theorem)
この定理のため、OLSは最も有用かつ有名な推定方法としてまず最初に使われるのです。
Better estimator is unbiased has the smaller variance.
まず、よい推定器とはバイアスが小さく、分散が小さいものと定義します。
ベスト、というのはつまり、バイアスがなく、分散が最小であるという意味になります。
上記で見たように、仮定1-3が満たされているときのOLSはconsistent and efficientです。これが分散がなく、分散が最小を意味し、OLSがbestであると示すことができるのです。
(分散が最小である証明は省略しますが、ある別の推定器を想定し、それらすべてより小さい、と示すことで証明できる)
これをガウス=マルコフの定理(Gauss Markov Theorem)といいます。
