基本の基本、最小二乗法OLSについて Econometrics
Ordinary Least Square Estimation (OLS)
Let's begin with OLS. さて、計量経済学でまず最初に扱うのは、最小二乗法 Ordinary Least Square Estimation (OLS)。
We first want to investigate the relationship between X and Y.
To answer this question, we will use a Linear model in paramaters.
あるXとY、2つのデータがあり、その正しい関係性(因果)を知りたい、というのがこの計量経済学の目的でした。そこでまず使うのが、直線モデルです。ここでは、モデルの意味と、その計算を見ていきます。
Model
まず、私たちはyを推定したいです。手元には母集団から独立無作為にとってきたサンプルのxとy(i.i.d)があります。(Independent and identically distributed random variables)
(iid についてはこちら)
そしてxとyから以下の式を作ります。
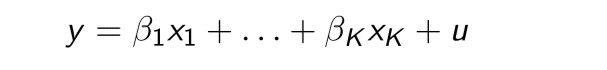
y, X1...k are observable variables. These are observed data.
Y is called dependent variable, since it depend on other variables. (Or, explained variable. )
X1...k is independent variables, since it does not depend on anything. Or, explanatory variable, control variable, regressors.
bata is the paramater we would like to estimate. It is called "estimator."
u is unobserved disturbance, called error term.
解説:
まず、モデルが考えているのは以下のようなグラフに直線を引き、Xが1上がるとyがどれくらい上がるかをβで表してます。
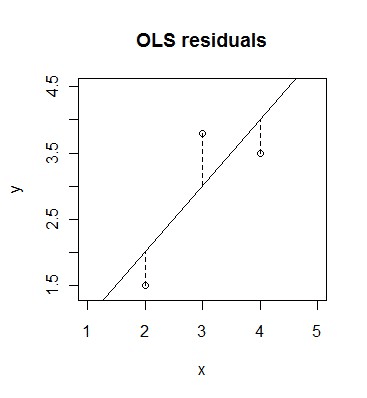
(出典 http://www.statisticalconsultants.co.nz/blog/total-least-squares.html)
例としては、上の図なら、xが1増えると、yも1増えてますのでβは1です。よって、
y = -0.5 + 1*x + u
みたいな感じですかね。If there is intercept (切片)、the first x1 become 1. x1=1, bata_1 = -.5, bata_2=1, x2=xと書き換えていることになります。
次に、y、x、uの呼び名が色々あり、混乱しますが、ただ複数いろんな意味からよんでるだけです。日本語だとyは被説明変数、xは説明変数、独立変数など。xをregressorsということもよくあります。βがestimatorというのも重要です.
Error term
uはerror termといい、xで説明できない部分の変化をこれで表しています。上記の図で言えば、一個一個の点と線の差がuです。x=2の点ならu=0.5。個人個人の性格、企業の経営能力、国の国土の影響や季節の影響など様々なものがこの場所に含まれて観測はできないエラーとして表示されます。
このuはデータを無作為にとっていることから、そのエラーの値は同様に無作為にデータの中に散らばっている(分布している)ということで、ある数人が0.5なら他の数人がー0.5というように、すべて足すと0になるようになっているだろうと仮定します。つまり、

ということです。逆に言えば、そうなるように直線を引きます。(こうすることで次の計算が楽になるんです。これは計量経済学で大切な仮定の1つ目になります)
Marginal Effect
先のβはmarginal effectと呼ばれます。
ほかの変数すべてが一定の条件において(ceteris paribus)xが1動いたとき、yがどのくらい変化するかを表している
という意味です。marginalは経済学で良く出現する単語ですので覚えておいてください。ceteris paribusについては別記事参照。
数学的には、βはこう書きます。
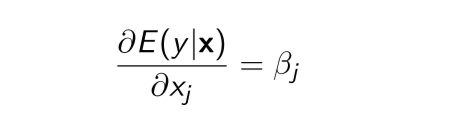
なぜ期待値Eを取るか,というと、yの本当の値はわからないから、です。(ここすごい一度悩んだ場所)
最初に言った通り、私たちはyを推定したいです。母集団から独立無作為にとってきたxとy(i.i.d)はサンプルなので、全部を使っても母集団の期待値までしかわからないです。(サンプルだとこうだから、xはこんなくらいの効果があるのかな、って感じ)
その期待値を知るため、最初のモデルの期待値を取ります。期待値をとるとこんな感じ。

ここでは、βxの期待値が取れていて、uが消えています。
まず、xの条件付き(conditional on x) で期待値を取りました。そのため、βxはβは定数、自分自身の条件付き期待値は取り外せるので、
E(bata x | x)=bata*E(x | x)= bata*x
となり、期待値が取れてます。
またuに関しては、以下の仮定を置かれているため、消えています。

再度いうと、xとyは独立に無作為にとってきたデータのため、もし本当に独立なデータなのであれば、error termはxによって変化しない、といえます。
逆に変化する例というと、全国の人を母集団とした所得と貯蓄の関係を知りたいときに、もしBMWの顧客リストからデータを取ってきた場合、みんなの所得はすでに高額なのでこれはiidとは言えません。すると、ここから得た所得が1万円あがったときの貯蓄額への影響は、バイアスがかかっており、本当にすべての国民からデータを取ったときに比べてこの影響はすごく小さくなっているかもしれません。なぜなら、例えば1億円所得がある場合と、2億円所得がある場合の貯蓄を知っても、それは性格などに依存しますし、あまり所得と貯蓄の関係も大きくないかもしれません。この時、E(u|x)は0ではないです。
ということで、βは
a derivative of Expectation of y conditional on x with xj
xの条件付き期待値yをあるXjで微分したものがβj
といえます。まあ微分はそもそも限界値を出すので、もしそれを知っていればすぐわかりますね。
もし、モデルがこんななら
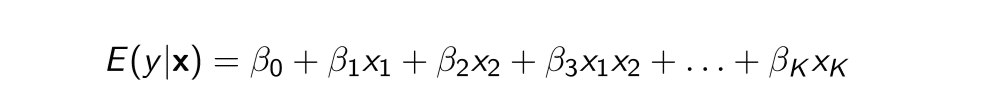
βはこうなる
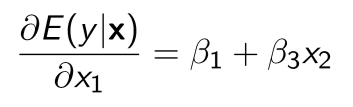
Computing
実際にβを求める際には、行列を使います。わからなくても大丈夫ですが、xが正則行列である必要があるという仮定が計量経済学を通して大事になる仮定2つ目になります。
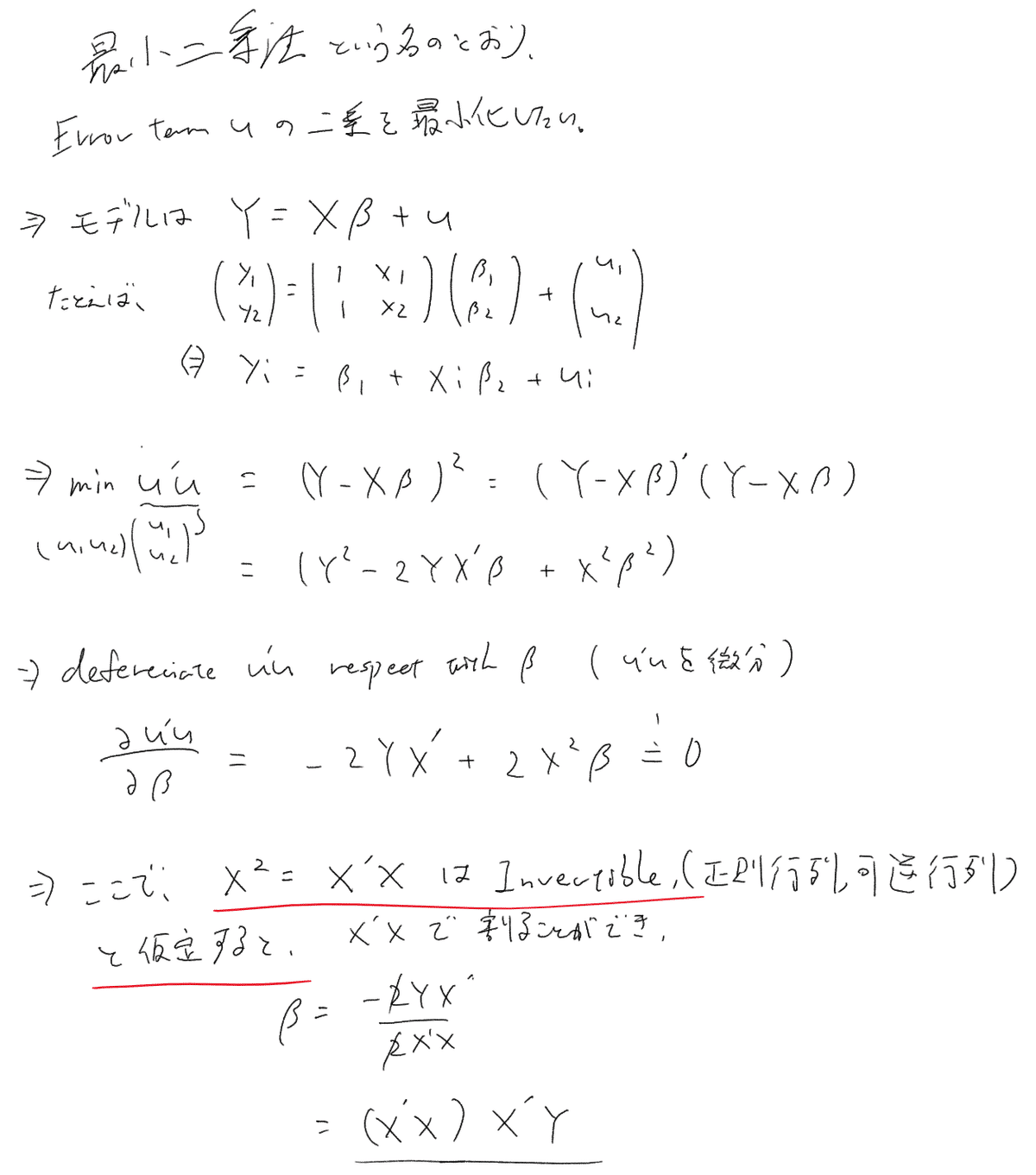
ここには詳しく書いてあります。
Lemma
あるmatrix(行列)がInvertible(正則行列)であること=The matrix is of full rank(行列のランクが最大)
であるので、この条件は一般に後者のfull rankの方、もしくは
The matrix is of Full rank = The matrix does not have any perfect multicollinearity(多重共線性).
より、No perfect multicollinearity(多重共線性がない)という条件としてかかれます。(証明省略)
まとめ
モデルはこんな形。
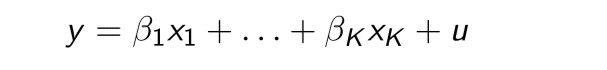
Y is called dependent variable, explained variable.
X1...k is independent variables, explanatory variable, control variable, regressors.
bata is called "estimator."
u is called error term.
βはまた、marginal effectと呼ばれ、計算の際には以下の2つの仮定を置くと、計算できる。
1.expectation of error term conditional on x is 0.
2. The matrix of x has no perfect multicollinearity. (多重共線性がない)
