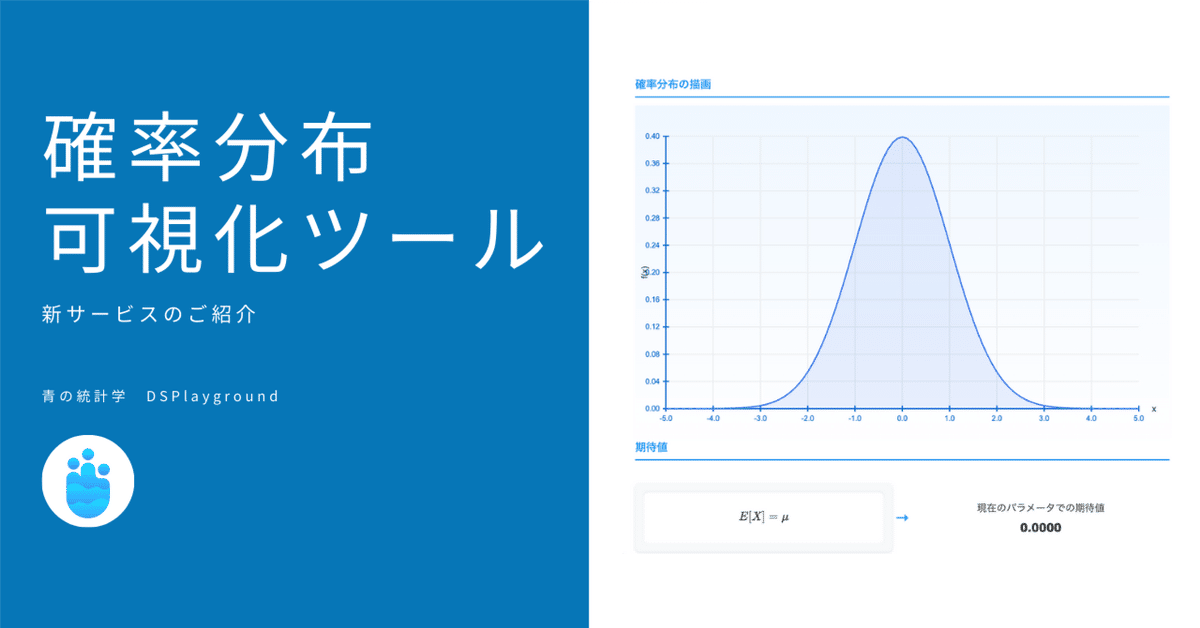
確率分布可視化ツールを作りました!
こんにちは、青の統計学です。
今回は、新しいツールを作ってみたので記事を書きました。
データサイエンスにおいて、確率分布はあらゆるモデリングの根幹を成す概念です。ビジネスの意思決定から学術的な研究、機械学習アルゴリズムの設計に至るまで、「どのような分布を想定するか」がモデルの解釈や精度を大きく左右します。

しかしながら、確率分布とひと口に言っても、
などなど、特徴は多岐にわたります。
公式や教科書の解説を読んでも、“実際にグラフがどう変わるのか”がピンと来ないという方も多いはず。
そこで!こうした分布の形状変化や性質をビジュアルで簡単に確認できる新ツール、「確率分布可視化ツール」をリリースしました。
本記事では、ツールの概要と活用シーンをお伝えします。
Xでも紹介しています
確率分布可視化ツールをリリースしました!各確率分布のパラメータ調整に加え、その時の期待値も一応確認できます。統計検定の勉強や大学での講義の振り返りなど、いろんなシーンで役に立つと嬉しいです。https://t.co/8NmCdH0qTv https://t.co/GBbZCyK3aZ pic.twitter.com/O6iYTP5iMR
— 青の統計学-Data Science School- (@blue_statistics) January 24, 2025
2025/2/9 アップデート|3次元確率分布可視化ツールを追加しています。
確率分布可視化ツールをアップデートしました!3次元でシミュレーションができます。パラメータを自分で動かすと、分布がぬるぬる動いてカメラも自由に動かせます。立体的に確率分布の挙動がわかるので、イメージしにくい分布も理解が深まると嬉しいです。 https://t.co/pChgKmOEGe pic.twitter.com/jWQALuKtHj
— 青の統計学-Data Science School- (@blue_statistics) February 9, 2025
1. 分布の役割と可視化は大事だという話
1.1 データサイエンスでの分布の位置づけ
データサイエンスの多くの場面では、観測データの背後にある確率的プロセスを仮定し、その仮定からパラメータ推定や仮説検定を行います。たとえば、
線形回帰モデルで残差に正規分布を仮定する
ロジスティック回帰で二項分布を仮定する(最大対数尤度の背景には二項分布の考え方がある)
Poisson回帰やNegative Binomial回帰でカウントデータの発生メカニズムを説明する
といった具合です。これらのモデルを成立させるために、実際にどの分布を想定するかは、データの性質や仮定したいモデルの特性によって左右されます。
1.2 教科書だけではつかみにくい「形」のイメージ
しかし、多くの教科書や記事で登場する分布の紹介は、数式や一般的な解説がメイン。実際にパラメータを「試行回数」「成功確率」「形状パラメータ」など色々いじってみないと、どのようにグラフが変形するのかはなかなか直感的に捉えにくいものです。
そこで“目で見て、分布の振る舞いをつかむ”というステップは、数式理解の補完として大事だと思うわけです。
2. 「確率分布可視化ツール」の特徴
2.1 20種類以上の分布に対応
今回のツールでは、一般的によく用いられる正規分布、二項分布、ポアソン分布はもちろんのこと、ベータ分布、ガンマ分布、ロジスティック分布、コーシー分布など、合計20種類以上の分布を切り替えられます。

大学での講義や教科書にたまに登場するけれど、自分で描画したことがない分布も多いのではないでしょうか? このツールを使えば、それらの分布のグラフをワンクリックで表示し、比較できるようになります。
2.2 “パラメータ変更”→“グラフがぬるぬる動く”
特に魅力的なのが、分布のパラメータ(平均や分散、形状パラメータなど)を変更した際に、グラフがリアルタイムでスムーズに変形する点です。
例えば、
二項分布で試行回数 $${n}$$を増やしたらどう形が変わるのか?
ベータ分布でパラメータ $${\alpha}$$ と $${\beta}$$を大きくした場合はどんな形状になるのか?
コーシー分布で位置パラメータやスケールパラメータを変えたら、山の中心や厚みはどう変化するのか?
こういった疑問を瞬時に視覚的に確認できます。まるでインタラクティブな教科書を見ているような感覚で、「あ〜、この分布はこんなに裾が重たいんだ」など、数値だけでは得られない学習体験(というか理解)が得られるでしょう。
2.3 分布の数式・説明文を併記
各分布の確率密度関数や、その分布が想定される状況などの簡単な解説もツール画面に併せて表示されます。

「数式」と「グラフ」と「用途」が結びついた状態で学べるので、単なる丸暗記ではなく、用途を踏まえて理解することが可能です。
2.4 期待値の算出
さらに、パラメータを変更したその瞬間ごとに、分布の期待値も表示されます。たとえば正規分布なら、平均 $${\mu}$$を変えると期待値がそのまま同値で変わっていく様子がグラフと数値の両面から実感できます。

「理論上の計算」から「視覚的なイメージ」へ一貫性を持って理解できるのは、学習効率を高めるポイントかと思います。
3. より専門的に使いこなすためのヒント
3.1 「分布の当てはめ」における第一歩
実務や研究においては、観測データに対して「どの分布を当てはめるとよさそうか?」をざっくり検討する場面があります。
たとえば、離脱率やCVRなどの割合データにはベータ分布が適しているかもしれないし、カウントデータが過分散を起こしているなら、単純なポアソン分布より負の二項分布のほうがモデルに適切かもしれません。

このへんの論文でも、同じようなモチベーションで負の二項分布をモデルに採用していたりします。
https://www.cell.com/immunity/abstract/S1074-7613(24)00273-5
こうした初期段階のアイデア出しを、あらかじめ可視化ツールで分布形状を俯瞰しておくと、「このタイプのデータなら、だいたいこの辺の分布を試してみよう」という指針が見えてきます。
3.2 Bayesianモデリングの直感にも
Bayesianアプローチを学ぶ際、事前分布としてベータ分布・ガンマ分布などを設定する理由が教科書に書かれていますが、実際にそれらの分布形状がどう動くのかを把握しておくと、事前情報の反映の仕方がより明確になります。
例えばベータ分布で「$${\alpha=1, \beta=1}$$」の場合は一様分布、「$${\alpha=2, \beta=2}$$」の場合は中央付近に集中した分布、など視覚的に理解しておくと、Bayesian推定やベイズ更新のプロセスも腹落ちしやすいでしょう。
3.3 教材としての活用
大学や専門スクールなど、統計学の初学者向け講義の場で活用いただくのもおすすめです。講義中にプロジェクターやオンライン共有で分布のパラメータを変え、動きに合わせて解説すると、受講者の理解度が飛躍的に向上します。
「数式だけだとわかりにくい……」という声は非常に多いので、こうしたツールを教材として取り入れることで、統計学の敷居をぐっと下げることが可能になるかと思います。
4. 今後:ABテスト・サンプルサイズ設計ツールへ
確率分布可視化ツールはあくまでツールの一つにすぎません。
このアプリ内では、今後さらに、
ABテストにおける統計的有意差の検証やベイズ更新を可視的に確認できるツール
必要サンプルサイズを、効果量や有意水準などから直感的に試算できるツール
などをリリース予定です。こうした機能は、統計検定を学ぶ学生だけでなく、ビジネス現場でアクションを起こすマーケターやデータアナリストにも大いに役立つはずです。というか自分が使いたい。
特にABテストはWebサービスやアプリ開発の現場で日常的に使われますが、その設計・分析は「どの確率分布を想定しているか」を理解しているか否かで結果の解釈が大きく異なります。
最後に
もしツールを使ってみて「面白い!」「こうしたほうがもっと良くなる!」と思っていただけましたら、ぜひ問い合わせ欄からFBをいただけると幸いです。
今後のアップデート情報なども随時発信していきますので、どうぞお楽しみに。これからも「青の統計学」をよろしくお願いいたします!
ツールへのアクセスリンク
確率分布可視化ツール(青の統計学)
ツールボタンから遷移してください。
グラフを動的に描画するので、スマホだとみづらいです。PC推奨です!
いいなと思ったら応援しよう!

