Go Exercise: Equivalent Binary Treesへの挑戦　その１

やっとというか、とうとうというか、ここまできました。ラスト二つのエクササイズです。ラスト二つはGoの並行処理を利用した問題になっています。ゴルーチンてやつですね。正直ゴルーチンの概念を理解するのにもかなり時間がかかったので、このエクササイズを解くのも時間がかかると思います。なので何回かに分けて残そうかなと思います。

問題の整理

英語のサイトをときには翻訳機を使い、ときには他の人が解説しているサイトをのぞき(もちろん答えまでは見てません。)でやっているので問題を理解するまでで一苦労です。ていうか日本人でTour Of Goの解説してる人英語できるのが普通なのか問題の説明もなしに答えのコード載せている人ばっかりです(これだから頭良い奴は…)。

なので問題の整理からしていきます。問題文が２ページに渡っているので分けて説明します。

まずは俗に言う二分木の説明と今回のエクササイズでの二分木を実装する型の紹介です。二分木についてはググればすぐ出てくるので説明は割愛します。

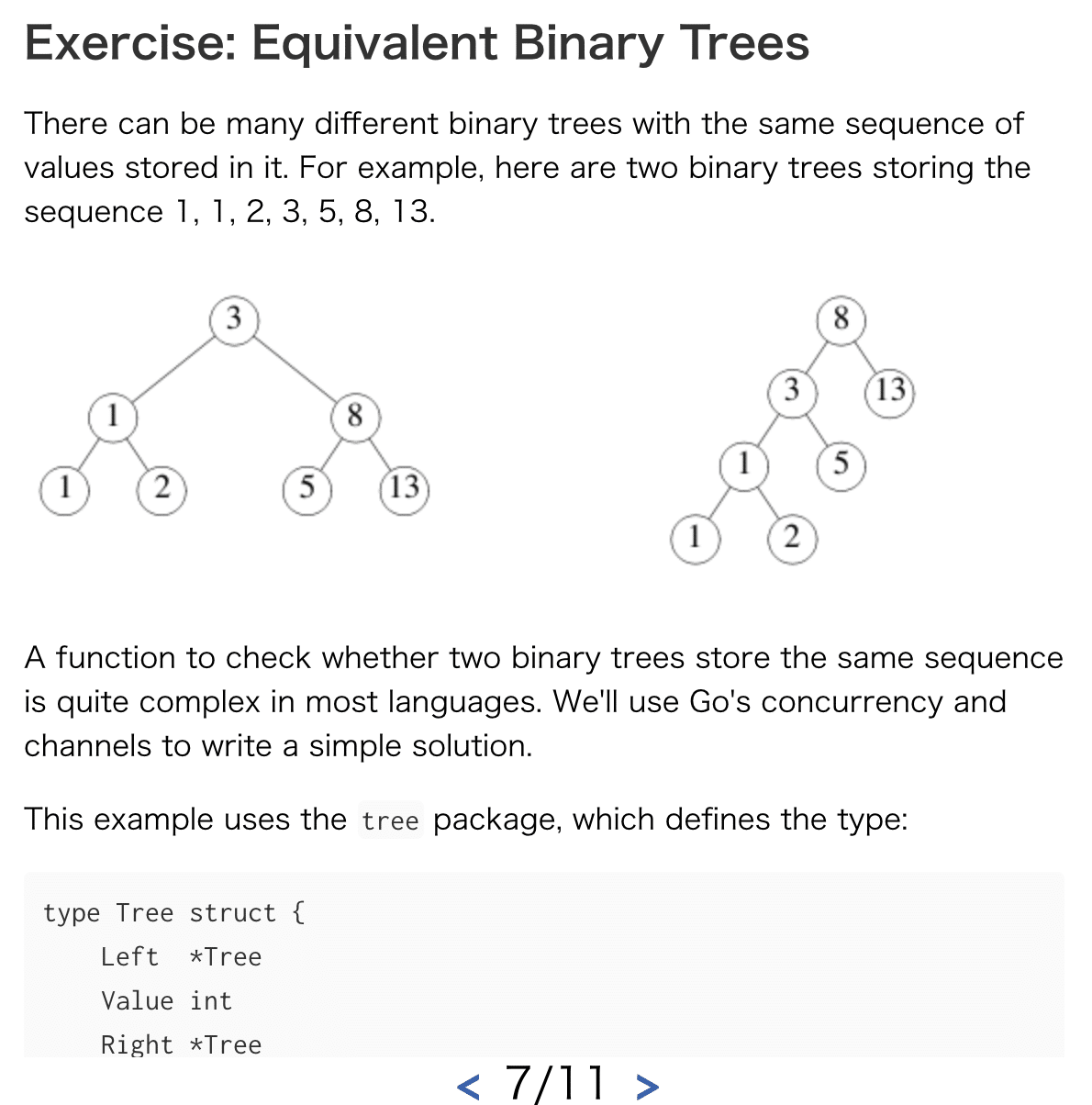
次のページは今回の課題である二つ二分木が同一とみなせるかを判定するプログラムの実装手順です。もちろんゴルーチン、チャンネルを使用して実装します(ゴルーチンを使うと他の言語より簡単に実装できるらしいです。簡単とは？)
流れとしては、

1.  二分木を探索して値を返すWalk関数
2.  Walk関数をテストしてみてチャンネルから期待した値(1, 2, 3, ...)がプリントされるか確認
3.  Walk関数から返されたチャンネルが等しいかどうかで二つの二分木が等しいかどうかをチェックするSame関数を実装する
4.  Same関数をテストし、ちゃんと期待通りの実装になっているかを確認

まずはゴルーチンを使わずに探索してみる

確認のため単純にTree型の変数をプリントで出力してみる

func main() {
	t := tree.New(1)
	fmt.Println(t)
}
実行結果
((((1 (2)) 3 (4)) 5 ((6) 7 ((8) 9))) 10)

どうやら単純に出力するとかっこでネストした形で表現するみたい。

次に、適当に思いついたロジックで探索するWalk関数を実装してみる。単純に再起呼び出しで木の下の方まで探索して行く。自分で実装しておいてアレなのだが、どこから表示されるかわからなかったので深さを表示するようにした。

func walk(t *tree.Tree, n int) {
	n++
	if t.Left != nil {
		walk(t.Left, n)
	}
	if t.Right != nil {
		walk(t.Right, n)
	}
	fmt.Println("深さ:", n, "値:", t.Value)
}

func main() {
	t := tree.New(1)
	fmt.Println(t)
	walk(t, 0)
	u := tree.New(2)
	fmt.Println(u)
	walk(u, 0)
}

実行結果
((((1 (2)) 3 (4)) 5 ((6) 7 ((8) 9))) 10)
深さ: 5 値: 2
深さ: 4 値: 1
深さ: 4 値: 4
深さ: 3 値: 3
深さ: 4 値: 6
深さ: 5 値: 8
深さ: 4 値: 9
深さ: 3 値: 7
深さ: 2 値: 5
深さ: 1 値: 10
((((2) 4 (6)) 8 (10 (12))) 14 ((16) 18 (20)))
深さ: 4 値: 2
深さ: 4 値: 6
深さ: 3 値: 4
深さ: 4 値: 12
深さ: 3 値: 10
深さ: 2 値: 8
深さ: 3 値: 16
深さ: 3 値: 20
深さ: 2 値: 18
深さ: 1 値: 14

図で表すと以下のような感じだと思います。

これで構造が掴めた(多分)ので次はちゃんと順番に表示するようにWalk関数を実装しなおします。