
interval likelihood ratio: 診断精度研究で連続変数や3カテゴリー以上の順序変数を扱う時,二値化して感度,特異度で表現するよりもinterval likelihood ratioを使いましょう
診断精度研究では感度,特異度で精度が示されることが多いです。あり,なしの評価であればこれでまったく問題ありません。しかし,連続変数や順序変数を扱う場合,どこかでカットオフ値をひいて二値化して感度,特異度として表現するのは情報が失われてしまってもったいないです。
二値化は情報量が失われる
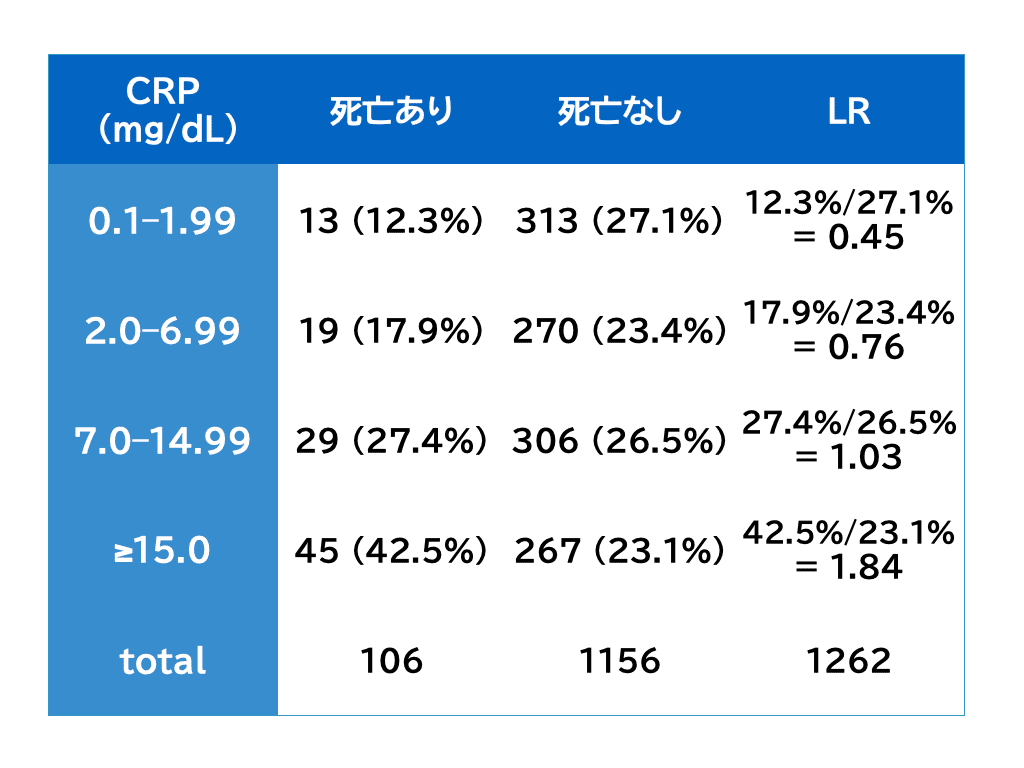
敗血症疑い患者の血清CRP値と30日間死亡を例に挙げます。
CRP値を層別に分けた場合の30日間死亡割合が以下の通りだったとします。

各カットオフ値での感度,特異度は以下の通りです。
CRPが1.0だった場合,感度87.7%,特異度27.1%を採用すればいいのかもしれないですし,CRPが20だった場合は感度42.5%,特異度76.9%を採用すればいいのかもしれません。
では,CRPが10だった場合どの数字を採用すればいいのでしょうか?10は≥2でもあり,≥7でもあります。どっちらのカットオフを採用すればいいのでしょうか?
10に近い方の7でしょうか?

論文によっては,感度重視で,≥2のカットオフ値しか示されないこともあるかもしれません。その場合,2.1も20も≥2以上ですが,臨床的にどちらも同じ意味としてよいでしょうか?カットオフ値を2で二値化するのは2.1も20も同じとして扱うため,情報量が失われてしまいます。
感度,特異度は検査結果が陽性,陰性の場合は便利な指標です。
しかし,上の例のように連続変数だったり,高リスク,中リスク,低リスクのような順序変数だったりした場合,どこかでカットオフ値をひいて二値化してしまうと情報が失われてしまいます。
interval likelihood ratio
このような時に便利なのが,interval likelihood ratio (LR: 尤度比)です。multilevel LRやstratum-specific LRとも呼ばれます。
LRは,ある検査結果をもつ人のうち,病気のある人の割合を病気がない人の割合で割ったものと定義されます。
検査が陽性,陰性の場合,検査が陽性の時の陽性尤度比(positive LR),陰性の時の陰性尤度比(negative LR)は以下のように計算されます。


3層以上ある場合も同様に計算することによってinterval LRを求めることができます。
MedCalc
https://www.medcalc.org/manual/likelihood-ratios.php
を使うと↓のような感じになり,信頼区間も算出してくれます(有料で永久ライセンス549ドル,年間ライセンス179ドルとお高いので,フリートライアル中のものです)。

LRによる検査前後の確率の変動
LRが1ならば,検査前後の確率には影響ありません。
0.5〜2の間では検査前後の確率はあまり変わらず,
2〜5の時は検査後確率がまあまあ上がり(0.5〜0.2の時はまあまあ下がり),
10以上だとかなり検査後確率が高くなります(0.1以下だとかなり上がる)。
検査前確率が10〜90%の間では以下のような近似が成り立ちます。

LRから検査後確率を求めるには,
・検査後オッズ=検査前オッズ×LR
・オッズ=確率/(1−確率)
・確率=オッズ/(オッズ+1)
の関係から計算できます。手計算だと面倒なので,スマホアプリを使うとよいと思います。
例えば,MedCalXを使うと以下のような感じです。
https://apps.apple.com/jp/app/medcalx/id1041464932
(Faganのnomogramを使ってもいいんですけど,スマホアプリの方が簡単です)

統計ソフトによるLRの計算
統計ソフトを使ってLRを計算する場合は,各層のリスク比を計算するのと同じです(例はBNPと左心機能障害)。以下はStataを使ったものです。



リスク比を計算できればなんでもよいので,RでepiRを使うと以下のようになります。

interval LRについてもっと勉強したい人へ
以下の総説がわかりやすいです。
Grimes DA, Schulz KF. Refining clinical diagnosis with likelihood ratios. Lancet 2005;365:1500–5. https://www.thelancet.com/journals/lancet/article/PIIS0140673605664227/fulltext
Richardson WS, Wilson MC, Keitz SA, Wyer PC, Group ETSW. Tips for teachers of evidence-based medicine: making sense of diagnostic test results using likelihood ratios. J Gen Intern Med 2008;23:87–92.
