食塩水の文章題 【連立方程式】

［関連ページ］

このサイトのコンセプトは「平均点くらい取ろうよ」でした。
点が低くて悩んでるなら、悩まないくらいの点なら取ろうよ。

このコンセプトには「文章題」は合いません。
文章題なんて解けなくても平均点なら取れるしね！

だけど、できるんだもん。このくらい。
一番簡単に教えます。

食塩水の問題は「難しめの問題」として認識されています。
でも、「解き方を覚える」んじゃなくて「式の作り方を理解する」ことに集中すれば、食塩水の文章題はきっとできます。

そこまで難しくはないけど、説明はちょっと長め。
落ち着いて、ひとつひとつ見ていこうね。

（連立方程式の基本計算だけは練習してきてね）

ーーーーーー

さっそく問題です。

はい、だめー！笑

なんでかって、「今ちゃんと読まなかった」でしょ。
苦手な人の特徴は、文章というだけで雰囲気負けするというところです。

大丈夫。
丁寧に、もっかい読んでみよう。

８％の食塩水　と
５％の食塩水　を　混ぜて

７％の食塩水　を　作りたい。

２つの食塩水（８％と５％）　を
それぞれ何グラム　混ぜる？

という問題です。
こういうふうに区切って読めば、さっきよりは難しくないでしょ？

だから雰囲気に負けちゃだめです。
ひとつひとつゆっくり理解すればいいだけ。

・・・

さて。
文章題を解くときに、一番にやること。
それは「聞かれたものに名前をつける」ことです。

今回、聞かれているものは何？

８％の食塩水　と
５％の食塩水　を　混ぜて

７％の食塩水　を　作りたい。

２つの食塩水（８％と５％）　を
それぞれ何グラム　混ぜる？

聞かれてるのは「２つの食塩水（８％と５％）それぞれ何グラム？」です。だから、これらに名前を付けます。

　８％の食塩水　ｘグラム
　５％の食塩水　ｙグラム

これで名前が付け終わりました。

名前を付けるメリットのひとつが、「イメージしやすくなる」。

こんなふうに図も描けます。

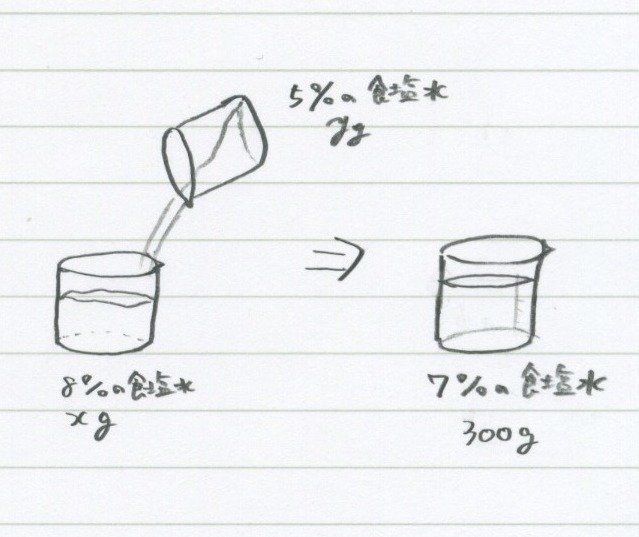
別にこんなふうに描かなくても、図は軽く、わかりやすく、です。

ーーーーーー

さあいよいよ立式（りっしき）です。
（立式＝式を作ること）

文章題は立式がほぼすべて。
だって解くのはもうできるもんね。

さっきの図をもう１回みてみようか。

ここから、何か式を思いつく？

・・・（待ちます）

はい。
１個は思いついたんじゃない？
１つはこういう式です。

これ！

ｘグラムとｙグラムを合わせたら３００グラム、という式です。
当たり前だよね。混ぜてるんだから。
この式はサッと作りたいです。

でも、連立方程式は式が２つないと解けないんでした。
あと１つ立式しなきゃ。

と思って、こう式を作った人。

アウトです。
「％」はたし算にできないんだ。
（そもそも８＋５＝７じゃないもんね）

やべえ。
行きづまりました。
食塩水がみんな苦手になるのは、この次の立式なんです。

ーーーーーー

っていうか％って何。
っていうか食塩水って何！

そこから考えてみます。

食塩水、つまり塩水（しおみず）です。
水に、食塩（家庭にある塩）を混ぜたやつです。

こういうこと。
ここから、少しレベルが上がるからね。よく聞いて。

じゃあ、食塩水の「％」って、何？

答えられたかな。
「％」は「食塩の濃度（濃さ）」を表しています。
つまり、しょっぱさだ。
食塩入れまくった方がしょっぱいよね。

ーーーーーー

ここでパーセントの話をサッとします。

こう分数で書くことができます。
そして「割合はかけ算」というのも覚えておいてください。
パーセントも割合のひとつです。

さあ！
ここに「５％の食塩水１００ｇ」を用意しました。
（さっきの問題とは無関係です）

「食塩水１００ｇ＝水と食塩を混ぜたら１００ｇになった」
ということです。
じゃあ、食塩はどのくらい混ぜたんだろう？

「割合はかけ算」なので、
パーセントは分数にして、かけ算すれば、出てきます。

５ｇ！
これが５％の食塩水１００ｇの中にある食塩の量だったんです。
図にするとこう。

（ついでに水の量は９５ｇだね。１００ー５です）

割合の計算、ちゃんとやりたかったらここでやってみてください。

ーーーーーー

これで、食塩の量が出せるようになったけど、あれ？
なんでこんなことやってたんだっけ。

もともと、立式を２つしたいと思ってたんです。
ひとつめは、食塩水の量をたして「ｘ＋ｙ＝３００」。
でも、パーセントをたした「５＋８＝７」はだめでした。

で今は、食塩水中の「食塩の量」の出し方を身につけました。

ねえねえ。
さっき食塩水の図を書いたけど

食塩水って元々「水＋食塩」だよね・・。

この食塩の量だけに着目したら、式ってできないかな・・。

しかも、食塩の量ってさっき・・・
「ｇ」に「割合」をかけて・・・

あれ？あれ！
これって式できちゃったんじゃない？

連立のもうひとつの式、できたじゃん！

ーーーーーー

並べて書いてみます。

おー！
できました！

「なんかめんどくさそう・・」って思うのは間違いだよ。
だって自分で式を作れたじゃん！
自分で式を作れたっていうことは、忘れても思い出せるということ。
ちょっとした応用くらいじゃ負けません。強いんです。

だってね。
食塩水の連立方程式の立式ってよく、

って書いてあるんだよ。
ふざけんなよ！
これは忘れたらおしまいです。
さっきのとは、全然、質がちがう。

だからこういう教え方は好きじゃないです。
でも、教科書にも問題集にもとっても多いから気をつけて。

暗記を無駄に増やして、勉強嫌いを増やすだけだと思ってます。
でも、みんなは、これを「覚えなくても」もう解けそうだよね。

ーーーーーー

じゃあ改めて！

目標の「２つの立式」が完成しました。
あとは勝手に名前を付けたので、１番最初にその宣言をします。
ここはめんどくさいけど、必ずね。

下の式には式変形が必要だね。
だけど約分しないように！

せっかく全部「１００分の」なんだから。
「×１００」しちゃえば全部消えます。

こういう感じ！
あとはいつもどおり解くだけです。もう安心。

おー。答え出ました！すごいよ！！
あの食塩水の問題だよ？すごい！

でも最後は「ｘ＝２００、ｙ＝１００」って書いちゃダメだからね。
だって「ｘ」も「ｙ」も勝手につけた名前だから。

「8%の食塩水200g、5%の食塩水100g」って書いたらおしまい。
聞かれたものは「2つの食塩水（8％と5％）それぞれ何g？」だったもんね。

ーーーーーー

結構大変だったけど、あと２問だけ、立式だけやります。

いったん問題を解いとくと、さっきよりめんどくさく感じないよね。
そういうもんなんです。最初はだいたいめんどくさい。

　って、あれ、水？？？

って慌てない。やることはなんだったっけ？
「聞かれたものに名前をつける」です。

つけました。
ちょっと図を描いてみようか。

さっきと同じで、ひとつめの式はこう。

ふたつめの「食塩の量」の式はどうしようか。

そのままやればいいんです。さっきのまま。
水は「０％の食塩水」と思えばいいんです。

「１００分の０」って結局「０」だけど、いいんです。
「やり方は一定の方がいい」です。迷わないからね。

このまま立式しちゃいます。

解くのは後で載せます。大事なのは「２つの立式」。

ーーーーーー

ラスト。
勘がいい人は何をやるか分かるかな？

はい今度は食塩です。
でもとりあえずやることがあったよね。

名前をつけました。
じゃあ、食塩はどうすればいいのかな。
食塩は「100%の食塩水」だと思えばいいよね。

ちゃんとしたやり方でやれば、「いつもと同じ」で出来るんです。
解答はまた後でね。

ーーーーーー

「食塩水」と「水」と「食塩」を並べて図示してみます。

もう大丈夫だよね！

ーーーーーー

これで食塩水の問題はおわり。
「立式を２つ」して「後はいつも通り」です。

ちなみに今回はやってないけど

「８％の食塩水に、５％の食塩水を１００ｇ混ぜて、７％の食塩水を作りたい。８％の食塩水と、７％の食塩水はそれぞれ何ｇになるか」

みたいな問題も、同じ解き方で解けます。
「聞かれたものに名前をつける」だけ。

今回の演習問題は、このページに出てきた全問題です。
こういう問題は、何問も解く必要はないから。
少ない問題でしっかり理解して解くのがいいです。
問題作るのがめんどうというのもあるけどね。

文章題をたくさん練習したいなら、
学校のワークで立式までを練習するといいです。
文章題は立式でほぼ答えだからね。
式だけ作って、そこだけ答え見て、合ってたらOKです。

［練習問題］（答えは下です）

［全ページに飛べるもくじ］

［次のページ］連立方程式文章題・速さと単位変換

［答え］