二次関数の「動点」問題（わかりやすく） 【ｙ＝ａｘ²】

［前のページ］二次関数（面積）

いよいよ二次関数も最終ページです。
つまり中学の関数がおしまい。
よくがんばったね。

このページの動点（どうてん）の問題は、
よく応用問題に載ってます。
実際、すごく簡単なわけではない。
（だから入試やなんかでよく出題されるんだね）

だけど順序立ててやればきっとできる。
このサイトは基礎が多めです。
だから基本的なとらえ方から、やってみるね。
このくらいできるようにするよ。いくよ！

ーーーーーー

二次関数のこのページを書き始めてから、
一次関数の動点問題も急きょ作ることにしました。

動点の問題は、一次関数だとか二次関数だとか、
そういうのはあまり関係ありません。
「動点の考え方」ができるかどうかが重要です。

二次関数に自信がある人はここから。
動点自体が不安な人は一次関数からやってみるのもいいと思います。

［一次関数の動点問題］

ーーーーーー

【二次関数の動点問題】

さあ問題です。

はい。
かなりやばそうな問題だね。
みんなが嫌そうな要素をだいたい入れました。

文章題で大切なのは、
問題の見た目でやられないこと。
落ち着いて、読みながらメモを取るなどして、読み進めていきます。

ＡＢ＝６ｃｍ、ＢＣ＝８ｃｍの長方形ＡＢＣＤがある。

点Ｐは辺ＡＢ上を秒速１ｃｍでＢからＡまで進み、
Ａに着くと止まる。

点Ｑは辺ＢＣ、ＣＤ上を秒速２ｃｍの速さで
ＢからＣを通ってＤまで進む。

点Ｐ、点ＱがＢを出発してからｘ秒後の
△ＢＰＱの面積をｙｃｍ²として

次の問いに答えなさい。
とのことでした。

ここからｙ（面積）をｘの式で表せよ、ということです。

ーーーーーー

【動点（ｘの変域）】

点Ｐと点Ｑの秒速も違うし、
点Ｐ止まったりするし。
もうどうしたらいいんだろう。

動点の問題が嫌な理由は「動く」から、でした。
動くのが嫌なら「止めればいい」じゃん。
という話は一次関数のときにもしました。
「写真を撮る」って言ったよね。

ただ、「いつ止めればいいか」の判断が、
今回はちょっと難しいです。
難しいポイントは２つあります。

　１．点Ｑが辺ＢＣから辺ＣＤに移るとき
　２．点ＰがＡに着いて止まるとき

このときにどうやら式が変わりそうだからです。
しかも点Ｐが止まるとき、
点Ｑが、ＢＣ上かＣＤ上か、もわからない。

だから今回は先に、ｘの変域（秒）を調べてみます。
まず点Ｐから（２点同時はむずかしいから）。

点ＰはＢから動くから、
Ｂにいるときはそりゃあ「０秒」です。

こうやって書き込みます。

そこからＰはＡに進むんだよね。
辺ＡＢの長さは６ｃｍ。
点Ｐは秒速１ｃｍ。つまり１秒に１ｃｍだから、
Ａに着くときは６ｃｍ分の「６秒」です。

これで点Ｐの動きが分かりました。

　０秒から６秒→辺ＢＡ上を動く
　そのあと→止まる

じゃあ続いて点Ｑね！点ＱもＢスタートです。

そこからまずＣまで進みます。

辺ＢＣの長さは８ｃｍ。
点Ｑは秒速２ｃｍ。つまり？
１秒に２ｃｍということ。

ってことは、
２秒で４ｃｍ、
３秒で６ｃｍ。
（秒の倍だね）

だからＣまで８ｃｍ進むには「４秒」。
（４秒×２＝８）

点ＱはそのままＣからＤまで進みます。

辺ＣＤの長さは６ｃｍ。
点Ｑは秒速２ｃｍなんだから、
Ｄまで６ｃｍ進むには「３秒」。
（３秒×２＝６）

Ｃまで、すでに４秒経ってるので、
Ｄまでは４＋３で「７秒」だね。

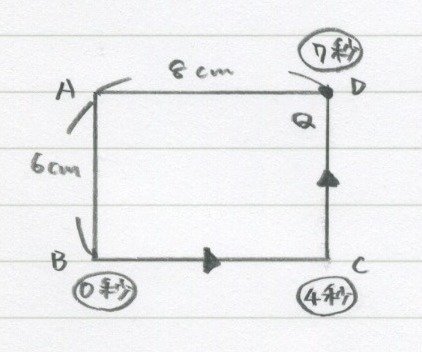
これで点Ｐと点Ｑの進み方が出ました。

　点Ｐ・・ＢＡ上（０秒から６秒）
　　　　　そのあと点Ｂで止まる

　点Ｑ・・ＢＣ上（０秒から４秒）
　　　　　ＣＤ上（４秒から７秒）

ということです。

点Ｑは７秒まであるのに、点Ｐは６秒まで。
その６秒から７秒の間に点Ｐは止まってる、
ということじゃないかな？

つまりこの問題の区切りは

「４秒（点Ｑの動く辺が変わる）」と
「６秒（点Ｐが止まる）」の２箇所です。

　０秒から４秒まで
　４秒から６秒まで
　６秒から７秒まで

をやれば、この問題は解けそう。
秒はｘだったから、こういうのを

　０≦ｘ≦４
　４≦ｘ≦６
　６≦ｘ≦７

というふうに書くのでした。

ーーーーーー

【① 点ＱがＢＣ上】

これでやっと解くことができます。
まずＢＣ上だから「０≦ｘ≦４」です。

動点の問題は動くから難しい。
だから「止めればいい」んだよね。
それはつまり「写真を撮る」感じだよ。
それも一次関数のところで話してました。

そのシーンの図を描いてみると、
（動点問題は、このメモ図を必ず描きます）

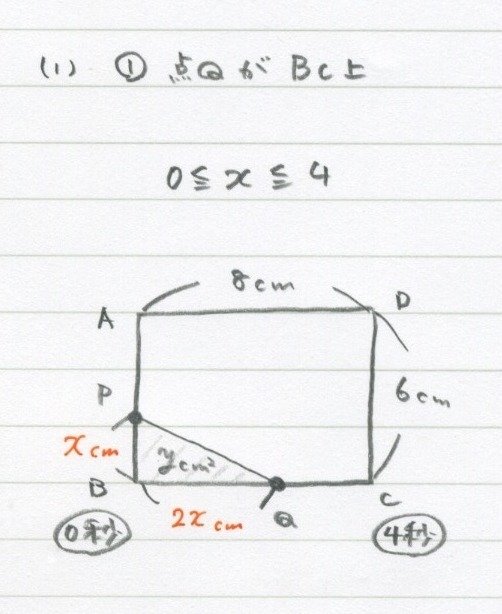
点Ｐは秒速１ｃｍだからＢＰ間は「ｘｃｍ」、
点Ｑは秒速２ｃｍだからＢＱ間は「２ｘｃｍ」でした。
図はフリーハンドでいいからね。

さあ。三角形の公式はこうでした。

最後に「÷２」より最初に「1/2」のほうがいいからね。

底辺も高さも求まってるから、
△ＢＰＱの面積はもう求められそうです。

求まったね！
なんと二次関数（ｙ＝ａｘ²）でした。

でもこれで答えじゃない。
最後に変域（０≦ｘ≦４）を載せて答えです。

こんな感じ！

ーーーーーー

【② 点ＱがＣＤ上】

点ＱはＣＤ上を「４秒から７秒」で動くんでした。
だけど、

「４秒から６秒まで」と
「６秒から７秒まで」で分けるんだったよね。

というのはさっきやったよね。
だから正確には

【② 点ＱがＣＤ上（４≦ｘ≦６のとき）】

です。　　
じゃあ動きを止めるよ！

こういう三角形になるからね。

↓みたいなミスはしないように。

△ＢＰＱがｙ、だからね。

あれ？
「２ｘ」って書かなくていいの？

そう思った人！「２ｘ」は、

Ｂスタートのここです。
このＬ字型のところが「２ｘｃｍ」。
今回は使わなそうなので書きませんでした。

三角形の高さは「底辺と垂直」。
だから図みたいに、
底辺ＢＰ（ｘｃｍ）に対して垂直なところ、
「８ｃｍ」が高さだからね！（よく見てね）

もう答え！

ーーーーーー

【② 点ＱがＣＤ上（６≦ｘ≦７のとき）】

じゃあ場合分けラストだ！
写真撮ります。

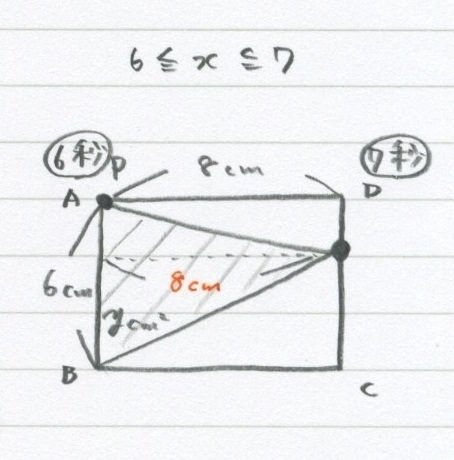
このときは点ＰはＡで止まってるので
ＢＰの長さは「６ｃｍ」で固定です。
（止まったほうが楽なんだ）

高さはさっきと同じ「８ｃｍ」だね。
じゃあ答えです。

まとめると

こんな感じでした。
最初の変域のメモができれば、できるということだよ！
（＝最初のメモができなければできない、ということ）

ーーーーーー

【（２）ｘ、ｙの関係をグラフに表しなさい】

じゃあ最後の問題です。
まずはさっきの式を一覧にします。

これを全部、
こういうグラフに書いていく。

まず「０≦ｘ≦４」です。
この区間は「ｙ＝ｘ²」で二次関数！
だから二次関数の描き方で

こうだね。
４秒までだけです。

（意味がわからなかったらここで練習ね）

そしたら「４≦ｘ≦６」で「ｙ＝４ｘ」。
一次関数ｙ＝ａｘ＋ｂの形してるから「直線」です。
（ｂ＝０だと思えば一次関数）

こういうのは、終点のｘ＝６を求めちゃうんです。
代入！

　ｙ＝４×６
　　＝２４

なのでその点を打って、

直線なんだから繋ぐだけ。

これだけ！

じゃあ最後。
「６≦ｘ≦７」で「ｙ＝２４」。
６秒から７秒の間はずっとｙ＝２４ということです。

終点（７，２４）に点を打って、結ぶだけ。

ほらこれで答え！
このグラフを見たら難しそう。
でも一個一個やったら、そこまでだったよね。

見た目でやられちゃダメだよ。
おしまい。

ーーーーーー

このあと比例と反比例も軽くやる。
でもここで一応、中学の関数はおしまいです。

中学の数学はだいたい、

１学期「計算」
２学期「関数」
３学期「それ以外」

という配分です（知ってた？）

それだけ関数のしめる割合は大きいからね。
得意にしとくと、なにかとお得です。
困ったらいつでも戻ってきてね。
誰より分かりやすく作ったからね。

練習問題は上の問題と同じ問題。
できるだろうが！がんばれ！

［練習問題］

［全ページに飛べるもくじ］

［次のページ］比例を飛ばした理由

［答え］