たった４つの作図（コンパスのつかいかた） 【垂直二等分線・角の二等分線・垂線】

このページは作図（さくず）！
作図ね、ちょちょいとしかやらないくせに、
入試で出たりするからね、みんなだいたい嫌がります。

でも中学の作図なんてたった４つだから。知ってた？
区別できるようにしていけば大丈夫です。

ーーーーーー

【作図を全部頭にいれてみよう】

最初に、４つを一覧にしてみます。
フリーハンドでいきます。

この４つ。
いったん描き方はどうでもいい。
「どういう道具があるのか」を把握してなければ、
何も解けないからね。

具体的には、
垂直二等分線と角の二等分線と垂線（２種）です。
これらをひとつずつ説明していきます。

ーーーーーー

【コンパスがどうしても苦手な人へ】

ちなみにコンパス下手なひと、結構います。
コンパス苦手なひとは、上から見ると

こんな感じで立て過ぎてることが多い。

コンパスをもっと寝かして、

ちょっと斜めにすると、
結構安定して、きれいに描けるからね。

ーーーーーー

【垂直二等分線】

まずは「垂直二等分線（すいちょくにとうぶんせん）」。

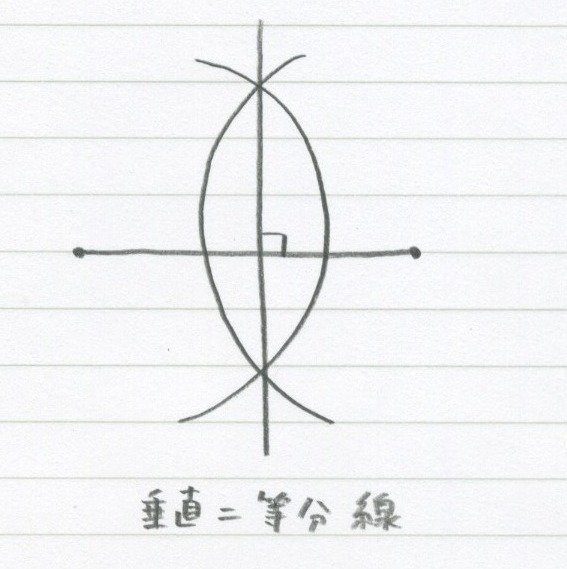
垂直二等分線はそのまま、
垂直に、二等分する線のことだね。

実際にやってみます。

こういうふうに２点あります。
とりあえずＡ、Ｂと名前を付けておきました。

この２点を結んで線分（せんぶん）にします。

（「直線」は永遠に続く線のこと。
　「ここからそこまで」という線は「線分」といいます）

ＡＢを線分にしたら、
コンパスを適当にＡからぐるりと引きます。

半円でいいです。
そしたら「コンパスの幅を動かさずに」Ｂからも引きます。

こういうふうに２つの円が重なるように。

こうなったらだめ。

一次関数（直線）でもやったように、
直線は２点ないと書けません。
重なると「２点」できてるよね（見てみて）。
だからうまく重なるように、コンパスの幅を設定してね。

で、その２交点を定規で結びます。

はい。
これで垂直二等分線です（ ┐の記号は垂直の印）

でね、だいたいみんなここでおわります。
結局、垂直二等分線がなんなのか分かってない。
だから応用がきかなくなっちゃうんだな。

垂直二等分線を「理解」しよう。
垂直二等分線は、ＡＢからのキョリが

ここも

ここだってもちろん

全部等しいんです。
（「＝」は「長さが等しい」という記号）

だから垂直二等分線は
「２点からのキョリが等しい」ときに使う作図だと
思っていてください（これ超重要）

今覚えてね。垂直二等分線は？

「２点からの距離が等しい」。

じゃあ問題だ。

ほらこうなると、突然何をしていいか分からなくなるでしょ。

でも「２点Ａ、Ｂから等しい距離にある」って書いてある。
なら「垂直二等分線」じゃん、ということです。

直線ｌ上にあるってところは、とりあえず無視していい。
とにかく「線分ＡＢを引いて、垂直二等分線書く！！！」

はい引きました。
そしたら使ってない条件「直線ｌ上」。
そのｌ上にあるのが「点Ｐ」だから、

ここが答えだということだね。
ほら「２点からの距離」にさえ反応できれば、
大した問題じゃなかったんだ。
（直線ｌのｌはたぶんライン（線）の頭文字です）

ちなみに今回の場合は

線分ＡＢは引かなくてもいいね。
いいんだけど、別に引いたっていい。

だからいつも引いとくのがいいと思います。
（必要なときもあるからね）

とにかく垂直二等分線は？

「２点からのキョリが等しい」だったね。

ーーーーーー

【角の二等分線】

じゃあ次、「角の二等分線」ね。

角の二等分線は、

もともとこういう∠ＡＯＢがあります。
この角を二等分しろ、と言われるわけです。

まずは

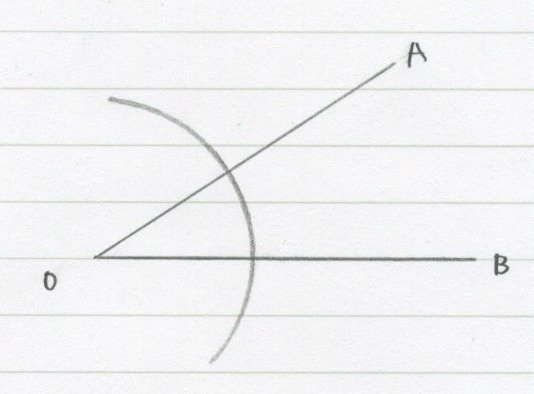
こういうふうに点Ｏからコンパスで半円を描きます。
そしたら、その半円とＯＡの交点からコンパスで

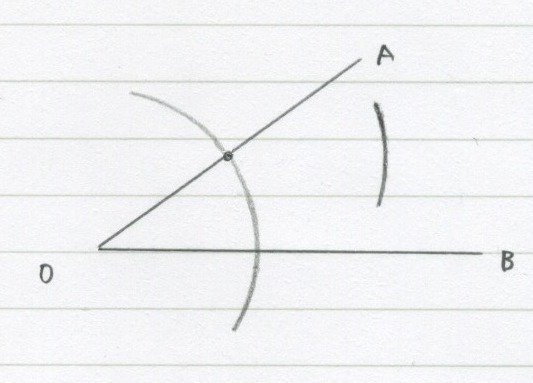
こう！
そしたら「コンパスの幅を変えずに」今度はＯＢの方から

こう！

そしたら直線は「２点あれば」引けるから、
「今の交点」と「点Ｏ」を繋ぎます。

これで「角の二等分線」完成です。
（ ● は角の二等分線マーク）

そして角の二等分線も「理解」だ。
角の二等分線は

ここも

ここも、
辺ＯＡ、辺ＯＢとの距離が同じです
（ちょっとむずいよね。わかる）

とにかく角の二等分線は
「２辺からのキョリが等しい」ときに使う作図です。

今覚えてね。
角の二等分線は？

「２辺からのキョリが等しい」でした。

なんとなく
垂直二等分線のほうが２辺っぽくて、
角の二等分線のほうが２点っぽいでしょ。
でも逆だからね。

もう一度。

垂直二等分線は、「２点からのキョリが等しい」。
角の二等分線は、「２辺からのキョリが等しい」。

今覚えてね。
完璧に覚えたら問題やってみましょう。

こういう問題。
辺ＡＢ上というのはいったん無視。
とにかく「辺ＡＣと辺ＢＣから等しいキョリ」ということは
「２辺からのキョリが等しい」ということです。

じゃあ辺ＡＣと辺ＢＣで角の二等分線引いちゃいます。

そしたら「辺ＡＢ上」で「点Ｐ」。

もう答えです。

あらためて、角の二等分線は？

「２辺からのキョリが等しい」ね！
これだけ覚えとけば解ける問題でした。

ーーーーーー

【垂線】

垂線（すいせん）。
その名のとおり「垂直な線」です。
垂線は２タイプあります。

垂直二等分線と角の二等分線には
「２点から」とか「２辺から」みたいな意味があったね

が、垂線は特に意味はありません。
ただの「垂直な線」です。

まずひとつめ。

線上に点Ａがあります。
この点Ａを通る、垂直な線を引きます。

まずこう。

点Ａを通る円を描きます。
線に交点が２つできればいいです。

この交点から、
さっきの角の二等分線の感じで、

こうして、そして（コンパスの幅を変えずに）

こう！

これでもう、直線を引くのに必要な２点できました。
交点と点Ａです。

これが垂線ひとつめ。

垂線２つ目。
今度は線と離れて点Ａがあります。

このＡを通る垂直な線を引きます。

まず点Ａからコンパスで

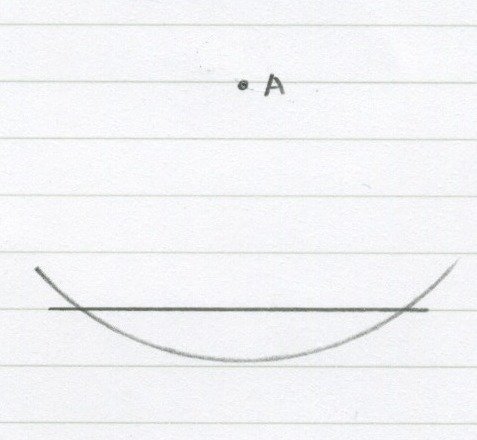
こう。
（いつも２点作ってるの分かった？）

そしたらさっきの感じ！

こうして

こう。
そしたら「この交点」と「点Ａ」を

結ぶだけ。
これが垂線ふたつめです。

ということで

この２つね！

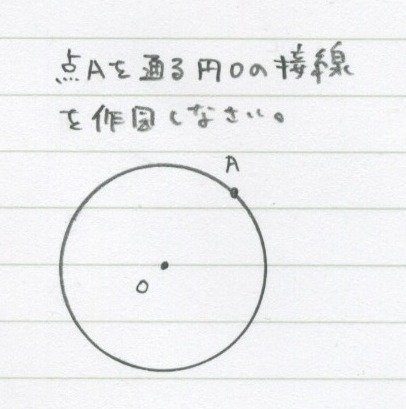
問題です！

「円の接線（せっせん）」とは

こういうふうに、円に１点で接する線のこと。
この接線は「円の中心から引いた線と必ず垂直」です。
ちょいむずかしい？

まあとにかく！
さっきの問題は

こんなふうに伸ばしたら、
あとは点Ａの垂線を引くだけ（さっきのひとつめ）。

こうして

こうして、こうして、

これで、接線完成です。
以上、垂線の解説でした。

ーーーーーー

【作図で大事なこと】

改めて４つ載せます。

作図で何が大事か分かった？

　①　この４つをちゃんと把握しておくこと
　②　垂直二等分線と角の二等分線の特徴を知っておくこと

これだけで解けます。

だから上の４つ、フリーハンドでいいから、
パッと描けるようにしとくこと！
忘れるともうおしまいなんだからね。

ちなみにこのページ作るのに

俺はこんなに描いてる！
せめて俺よりは描かないとね。できるようにしたいんだからね。

ーーーーーー

練習問題は、ここでやった問題に加えて、３つ。
この４つの道具だけで絶対にできるから、よーく考えて解いてね。
「２点から」「２辺から」がヒントね。

［練習問題］答えは下

（０）

作図の４パターンをフリーハンドで書きなさい。
また、垂直二等分線、角の二等分線は、
それぞれ「何からの距離が等しい」か答えなさい。

（１）

（２）

（３）

（４）〜（６）

［全ページに飛べるもくじ］

［次のページ］おうぎ形（円の一部と考える）

［次のページの準備］★割合について

［答え］

（０）

垂直二等分線は、「２点からのキョリが等しい」
角の二等分線は、「２辺からのキョリが等しい」

（１）

（２）

（３）

（４）〜（６）