一次関数のグラフの描き方、読み取り方（式→グラフ、グラフ→式） 【ｙ＝ａｘ＋ｂ】

さあ、ここから関数、つまり「グラフの問題」です。
中学の範囲では、比例、反比例、一次関数、二次関数の４つ。
高校の範囲も、この４つを「基礎」として、二次関数の応用、三次関数以降と進んでいきます。

なのでこのページでは比例から、
と思いきや、いきなり１次関数から教えます。
１次関数がちゃんと分かれば、他のもだいぶ分かるようになるから。
このページで、１からやってくので、安心してね。

関数はね、苦手になる理由も分かります。
分かるけど大丈夫。
実は、ただ「ひとつの考え方」を使うだけだから。
それに気づければ、クリアしたも同然です。

ここに出てくる「グラフの描き方」「グラフの読み取り方」は、
関数の全部に影響するくらい、かなり大切です。

余計な説明を省いて説明していくからね。

ーーーーーー

【座標】

関数を学ぶにはまず、
「座標（ざひょう）」の知識が必要です。

こういうやつだったね。

横の矢印は「横軸（よこじく）」とか「ｘ軸」、
縦の矢印は「縦軸（たてじく）」とか「ｙ軸」って言います。

こんなふうに「ｘ軸」と「ｙ軸」でできたやつを、
グラフ（とか「ｘｙ平面」とか）って言うと思っててください。

この平面は、地図みたいなもんです。
ここに点（座標）を打っていきます。

たとえば「ｘ＝２、ｙ＝１」の地点に点を打つと

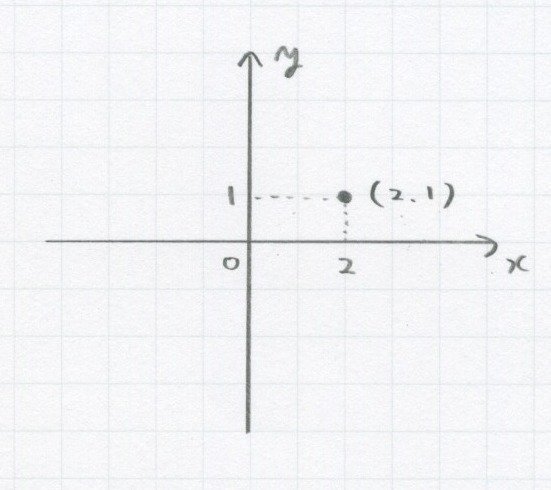
こんな感じです。
「ｘ＝２、ｙ＝１」のことを（２，１）と書くよ。

じゃあ（０，０）だったら、

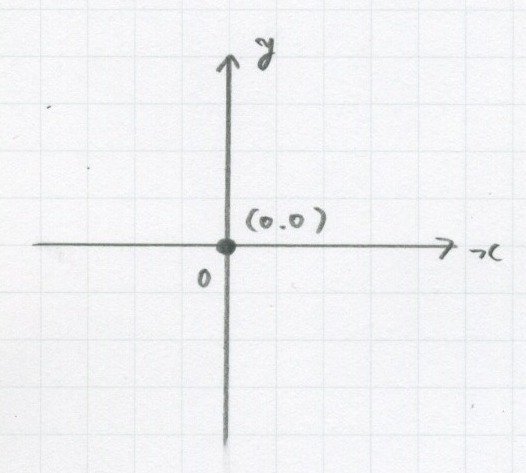
ここです。
この（０，０）のことを「原点（げんてん）」といいます。

（－１，３）なら、

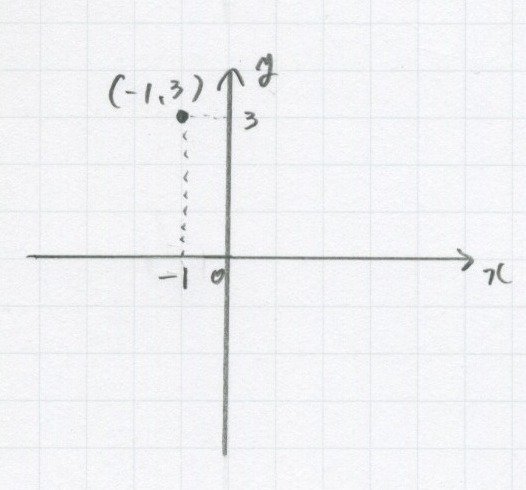
こうなるよね。
じゃあこの４点を打ってみよう。

（ｘ，ｙ）の順で数えるだけね。

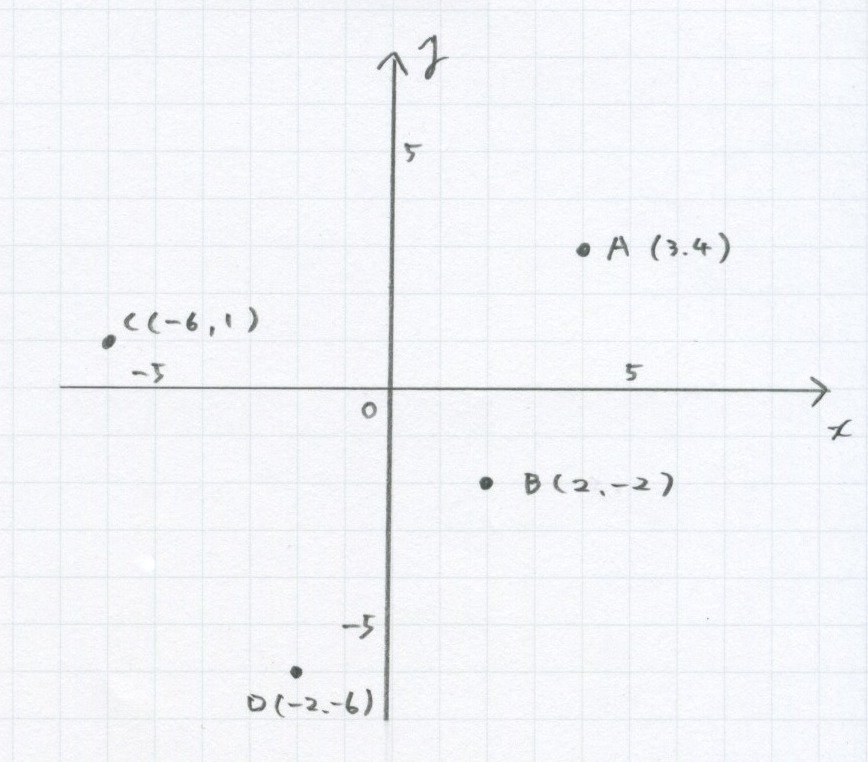
大丈夫そうかな？
この点のことを「座標」って言うのでした。

ーーーーーー

【座標軸プレゼント】

これからの説明は、
方眼ノートか、フリーハンドでも大丈夫なんだけど、
ちゃんと座標軸で練習したいな、と思う人用に
印刷用の座標軸プリントを作ってあります。

使いたい人だけ、印刷してやってみてね！

ーーーーーー

【一次関数とは】

さあ、じゃあいよいよ１次関数です。
とにかく１次関数はこれです。

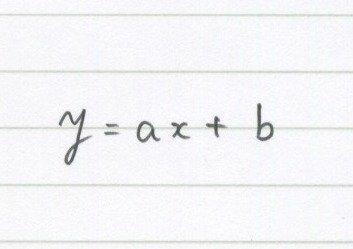
だからなんだよ！
って思うかもしれないけど、これが１番大切です。

とりあえず音読しまくって、覚えてくれる？
「ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ、ｙ＝ａｘ＋ｂ・・」ってね。

これを覚えないと何も始まりません。
だって１次関数って、ｙ＝ａｘ＋ｂなんだもの。

ーーーーーー

【一次関数のａとｂの説明】

「ｙ＝ａｘ＋ｂ」とは覚えました。
そして「一次関数は直線」です。
これをちょっとずつ説明していくね。

「ｙ＝ａｘ＋ｂ」には、文字が４つあるよね。
大切な文字は「ａ」と「ｂ」。
これが直線の特徴を決めます。

こうやって説明すると、ちょっとややこしい感じがするよね（特にａ）
とりあえずａは「傾き」、ｂは「切片（せっぺん）」だと覚えてください。

とりあえずこれでいいです。
傾きと切片って何やねんという質問を、今から答えていきます。

ーーーーーー

【切片ｂ】

まず「切片」についてやります。

ここに「ｙ＝ｘ」という直線があります。

さっきやった（０，０）の原点を通ってるね。
じゃあ式を少し変えて、
「ｙ＝ｘ＋２」にしてみます。

こうなります。
「ｙ＝２（ｙ軸の２）」を通ってるよね。
これが「ｙ＝ｘ＋２」の「＋２」の意味です。

じゃあ「ｙ＝ｘ－３」だったら？

そりゃあこうだよね。
「ｙ＝－３」を通っています。

並べて載せると、

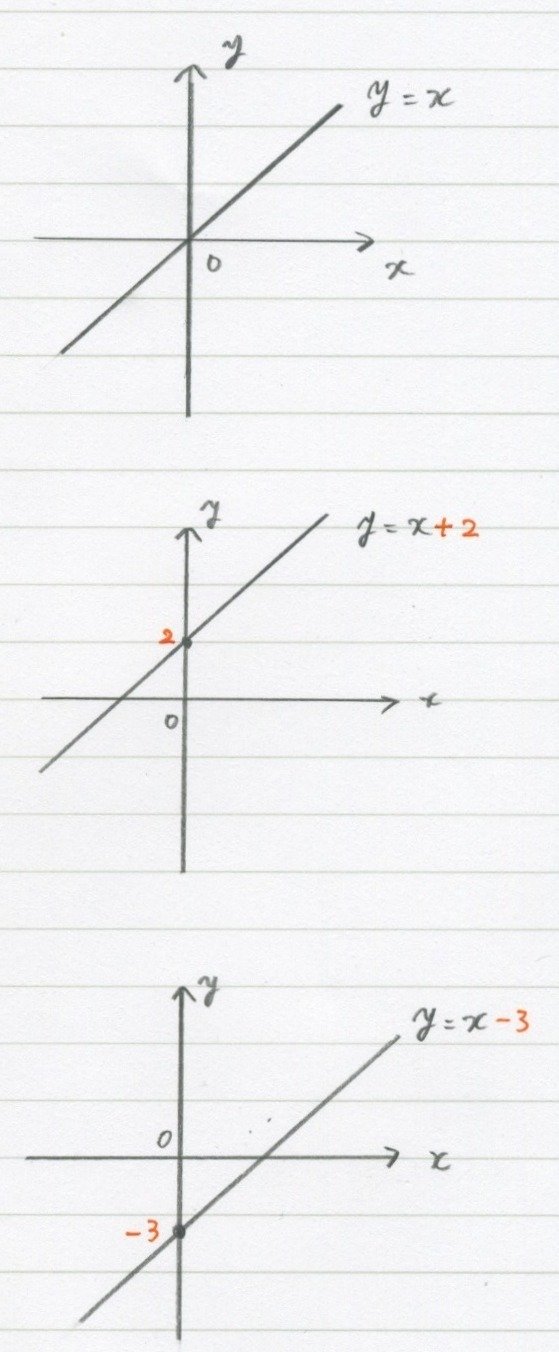
ただ「ｙ＝ｘ」が上下に移動してるだけです。

ｂの「切片」は「＋２」とか「−３」とか、
ただ「ｙ軸との交点」を表してるだけでした。

ーーーーーー

【傾きａ】

次はａだね。ａは「傾き」でした。
傾きって要するに「ななめぐあい」のことです。

さっきと同じ「ｙ＝ｘ」の直線があります。

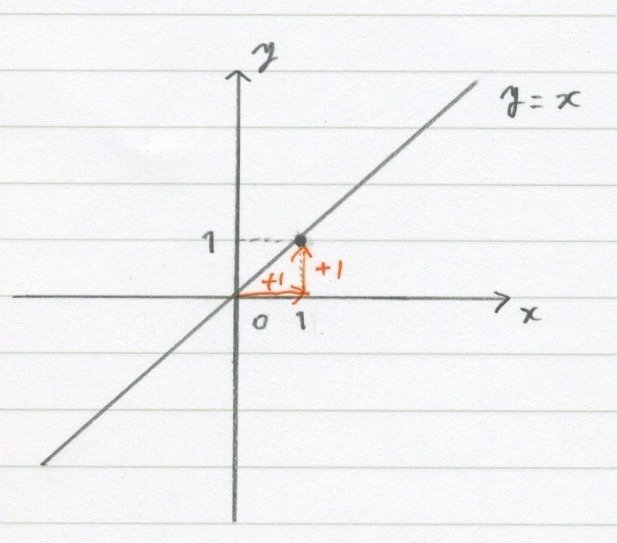
この直線に関する説明です。
ｙ＝ｘは「ｙ＝１ｘ」という意味だったんです。

１ｘの１は$${1=\Large\frac{1}{1}\normalsize=\Large\frac{+1}{+1}}$$という意味。

傾きは$${\Large\frac{+y}{+x}}$$だから、
原点から「横に１（ｘ方向）、縦に１（ｙ方向）」
の点を通ってるのが分かるかな。

やってるうちに分かるから、
とりあえず先に進みます。

$${\Large\frac{1}{2}\normalsize=\Large\frac{+1}{+2}}$$だから、

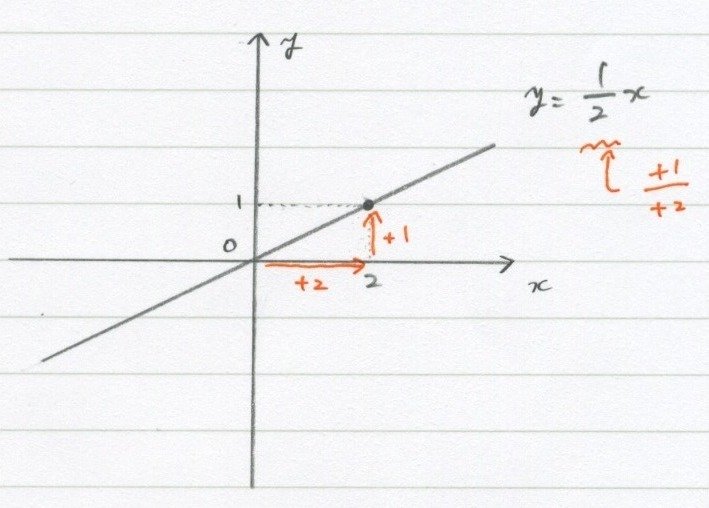
原点から「横に２、縦に１」の点を通ってます。

じゃあ「ｙ＝２ｘ」。

これは傾きが$${2=\Large\frac{2}{1}\normalsize=\Large\frac{+2}{+1}}$$だから、

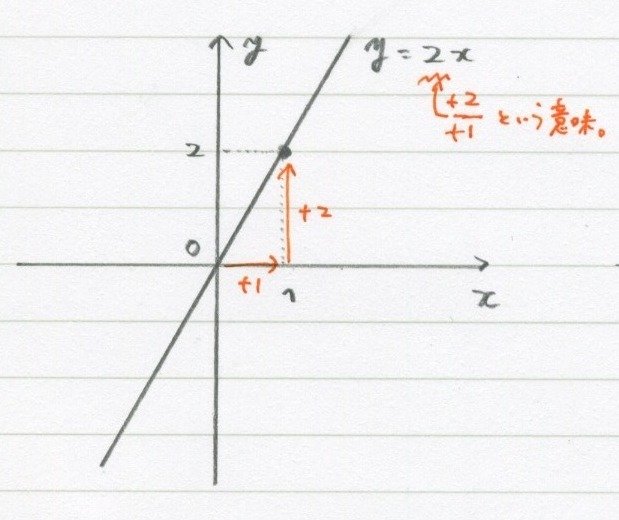
原点から「横に１、縦に２」です。

じゃあマイナスがあるパターンね。
「ｙ＝－３ｘ」。

傾きが$${-3=\Large-\frac{3}{1}\normalsize=\Large\frac{-3}{+1}}$$。
分数のときは「マイナスは上」だと思ってください。

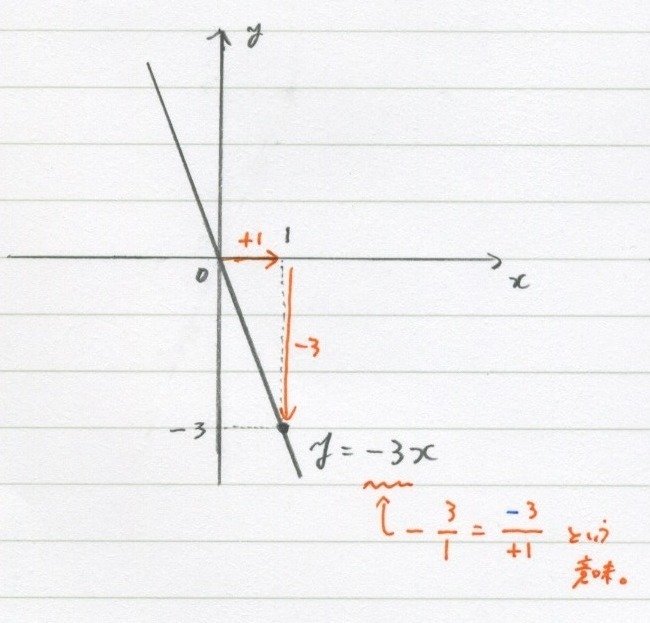
だから原点から「横に１、縦に－３」なんです。

じゃあ最後！

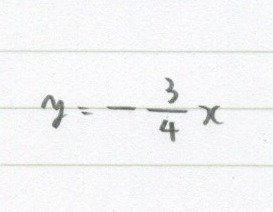
これはもう出来るかな。

$${\Large-\frac{3}{4}=\frac{-3}{+4}}$$だから、
原点から「横に４、縦に－３」。

これが「傾きａ」の解説でした！

ーーーーーー

【式→グラフ】

切片と傾き、わかったかな？
これを合わせれば、もうグラフが描けます。

例えば、

これならどうかな。
まず「切片」を打ちます。

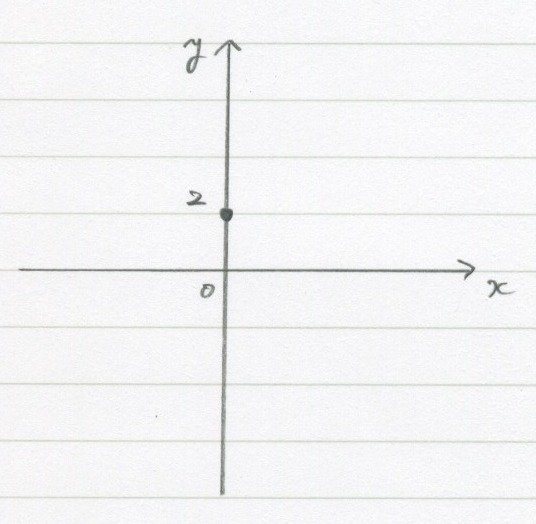
（方眼じゃないから「２」の位置は大体です）

次に傾き。
$${\Large\frac{1}{3}=\frac{+1}{+3}}$$だから、だから「横に３、縦に１」。
これからは「３行って１上がる」でもいいです。

そこに点を打ちます。切片からです！！！

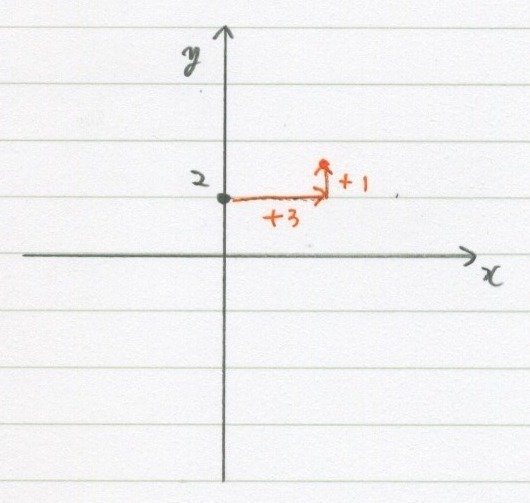
１次関数って「直線」だったよね。
直線は「２点」あれば引けます（１点では定規使えないもんね）

もう２点そろってので、引きます。

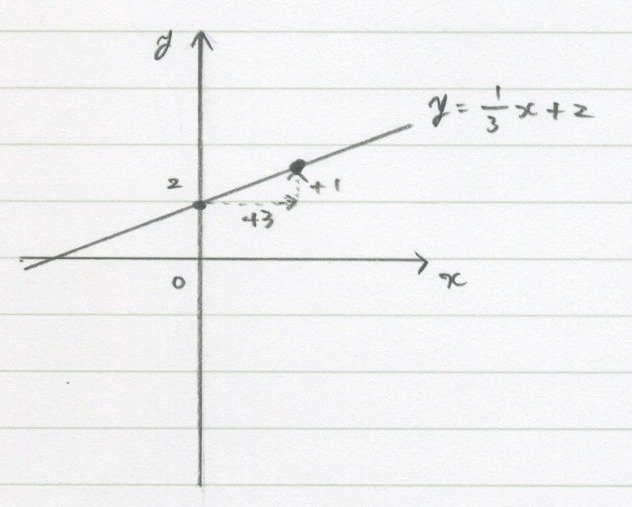
こんな感じ！

　① 切片を打つ
　② 傾きで点を打つ
　③ 線を引く

これだけ。
慣れれば余裕。
後で練習しようね。

ーーーーーー

【グラフ→式】

今は「式→グラフ」をやったよね。
今度は「グラフ→式」。
これができれば、実はもう一次関数の基礎はOKです。

また方眼でやるね。

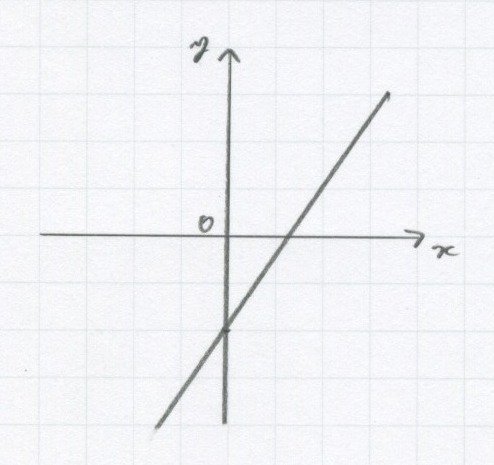
さっきグラフ描いたときと同じです。

① 切片を打つ

切片は「－２」だね。
「ｂ＝－２」が確定しました。

じゃあ後は傾きだね。

次は、切片の右側で「きれいな点」を探します。
きれいな点というのは、
ちょうど方眼の上を通ってる点のこと。

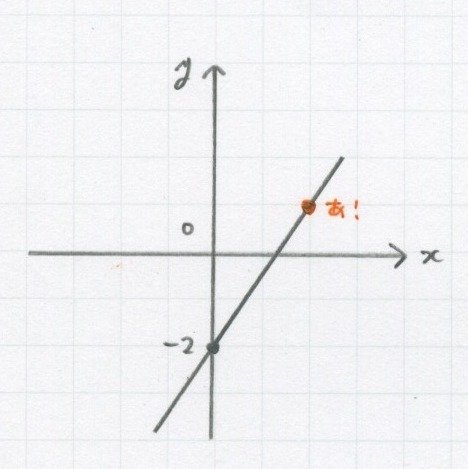
あ！見つけました。
切片から、ここまでいくのに、
どんな動きをするのかを考えます。

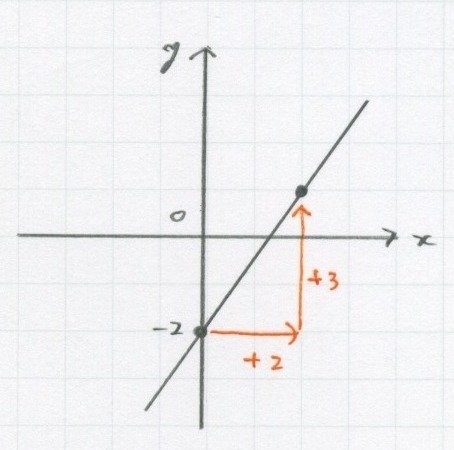
さっきの② 傾きで点を打つと、基本同じことをやってるよね。
そしたらもう傾きは分かるはずです。

「横に２、縦に３」、
つまり「２行って３上がってる」から

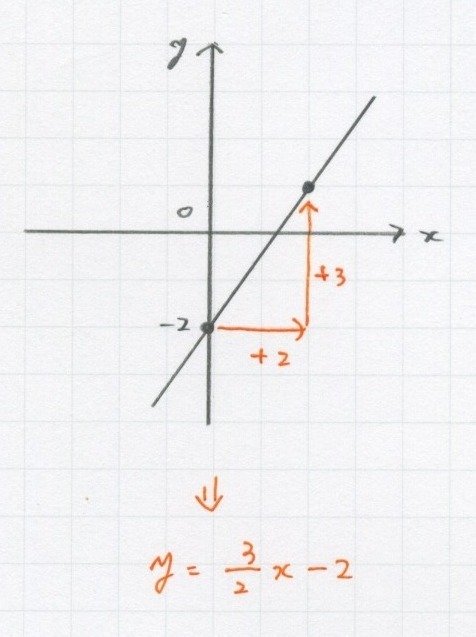
こんな感じで答えが出ます。
切片に点打って、きれいな点探して、傾き見つけるだけ。

じゃあもう１問ね！

最初に何だったっけ。「切片」だよね。

そしたら今度はきれいな点を探します。
（探すのは、右側がいいです）

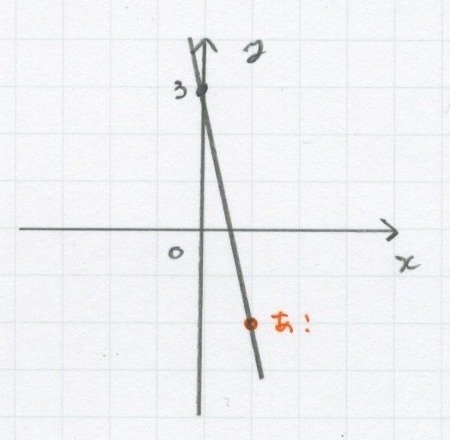
そしたら傾きを探して、

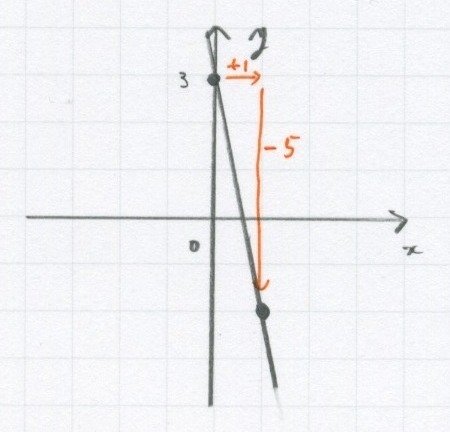
「１行って５下がる」って見つけたら、
もう答えです。

ということでした。
意外と簡単だね！

ーーーーーー

【定規はなるべく使わない】

今回は座標の練習だったから、
定規とか方眼ノートを使いました。
だけど基本的に定規は使わなくていいです。

定規使いすぎる人は、ちょっと気をつけてね。

「きれいに書くこと」と「理解すること」の、
どっちが優先順位が高いのか、よく考えてください。
「きれい」だけを大事にして、「理解」のことを忘れないようにね。
そもそもテストは定規使えないことが多いしね。

その、きれいで色がいっぱいの計算ノート、
きっと見返さないよ。

ーーーーーー

なんと、
あの難しかったはずの一次関数の、
基本はこれでおしまいです。

練習問題載せとくね！
全部できるように（方眼ノートなければ普通のノートでもいいよ）

［練習問題］答えは下

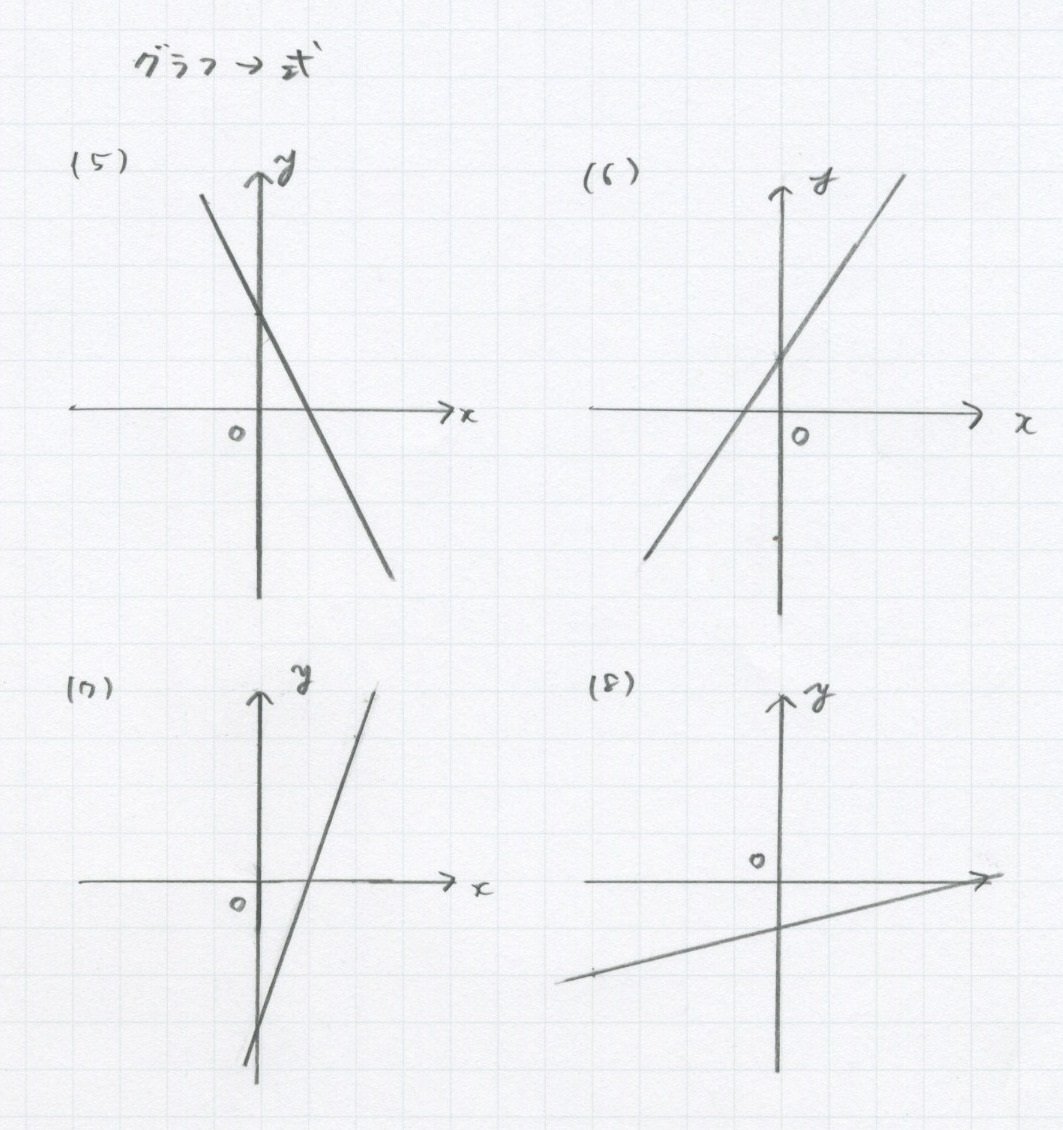
［全ページに飛べるもくじ］

［次のページ］１次関数（式の扱い）

［答え］