ミスが多すぎる約分の注意点 【式の計算】

［前のページ］

ここでは約分の注意点について扱います。
ここはとにかくミスが起きやすい！
じゃあまずこれを解いてみてください。

（ちなみに普通の約分を超得意にしたい人はこっちだよ！）

・・・

さあどうかな。
こんなふうに解いた人いない？

これは絶対やってはいけません。
どうしてか。

こういう分数は２行目みたいに「分ける」ことができます。
分けたあとに約分してるけど、「３ｙ」の方には「８」がまだ残ってるよね。

だからこうやって、長い分数のときに「４」にしてはいけないんです。
つまりこの分数は

この状態で答えでもいいし（これ以上約分できないから）、

分けて、これで答えでも、どっちでもいいということです！

ーーーーーー

次の分数もやってみよう。

さっきの「3y」が「4y」になっただけ。
はいはい、どうせこれもこのままで答えでいいんでしょ？

いいえ、違います。
なんででしょう？

「8」も「2x」も「4y」も（これを「項（こう）」と言います）
全部2の倍数だから「2」で割れるでしょ。
こういうときは「一気に」約分をしなくちゃいけないんです。

こういうふうに！

僕の中学のときの先生は「ハートの法則」って言ってました。
項（こう）を囲むとハートみたいに見えるからね。

ハートの法則

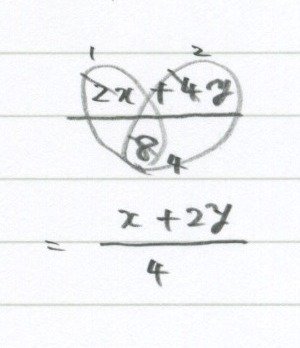
ハートの法則は分かりやすくて結構使えます！
ちなみにさっきの問題は

一気には約分できないよね。ハートで囲めない。
だからもう、これで答え。その違いです。

そして当然、さっきと同じで「分けて約分」してもOKです。

ーーーーーー

ごちゃごちゃしてきたかな？
さっきの問題とまとめてみようか。

① 長い分数のまま、「ハートの法則」が使えるなら使う
② 分けて約分

答え方は2つあるということです！

ごちゃごちゃした人は、②のやり方ならいつでも答えになるよ。
だから毎回②でもOK。
でもハートの法則も結構使えるんだよなー。

分子の項が3つ以上だとハートじゃなくなっちゃうけどね。でも使えるよ。

ーーーーーー

じゃあこの問題はどう？

今度は分子が「かけ算」です。
このときの解き方はこう。

こっちがこれか！！！って感じでしょ？
この問題と、さっきの問題が混ざってたから計算ミスが多かったんです。

ーーーーーー

でもなんでかけ算のときは「ハートの法則」使わないの？
そう思った人用の解説ね。

たとえばこの分数について。

この分数を約分すると

こうだよね。

ここで、元の式の「8」をちょっと分解してみよう。

たとえば「8」は「2×4」でもあるから、こういうふうにできるよね。
これに「ハートの法則」をやってみようか。

変なんなるでしょ？
でもさっきみたいに片方だけにすれば

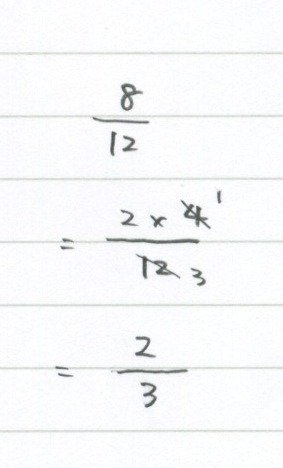
って、ちゃんと答えになります。

前に方程式で「かけ算わり算はひとかたまり」って書いたの。
かけ算わり算は「ひとつの数字」って思わないといけないんです。

「ひとつの数字」なのに、ハートの法則で、2回以上約分しちゃダメだよね。
これがかけ算に「ハートの法則が使えない理由」でした。

ーーーーーー

改めて2つのパターンを並べてみましょう。

この２つをちゃんと区別すること。
これを踏まえて次に進みます。
このページは演習問題なし！だけどものすごく大切なページでした。

（ちなみに「×（かける）」を小さめに書いてるのは「x（エックス）」との区別をするため。こういう工夫でミスが少なくなるよ！）

［全ページに飛べるもくじ］

［次のページ］長い分数に通分するやつ

［関連ページ］楽なのにミスが減る約分