ｙ＝ａｘ＋ｂの式の決定（計算ミスの減らし方） 【一次関数】

［前のページ］一次関数（式→グラフ、グラフ→式）

前のページで「式→グラフ」「グラフ→式」の両方をやりました。
ここは何より大事。
ここさえできれば、関数は結構簡単です。
逆に言えば、ここができないと何も出来ない。
関数とはグラフだからです。
マスターしておいでね。

ここでは式の決定！
前のページができてれば難しくはないよ。
苦手な人多いけど、こんなの余裕にしましょう。

まず。
一次関数ってなんだっけ？

ーーーーーー

【一次関数の式の決定①】

一次関数は

この式です。「ｙ＝ａｘ＋ｂ」です。
これがすぐに出ないとアウト。

この「ｙ＝ａｘ＋ｂ」は直線を表していました。
かつ、この中の「ａが傾き」「ｂが切片」だったね。

さて。
では問題です。

直線ってことは一次関数。
だから「ｙ＝ａｘ＋ｂ」だね。

んで傾きが３　→　ａ＝３ってことか。
切片が－４だと　→　ｂ＝－４ってことだ。

なんだこれ。

ａ＝３、ｂ＝－４のｙ＝ａｘ＋ｂってことでした。
なめた問題だったね。
でもこれが基本。簡単そうでしょ。

ーーーーーー

【一次関数の式の決定（ａを代入）】

次ね。

さっきよりはめんどくさそう！

さっきの問題はあんまりに簡単だったので書かなかったけど、
この「式の決定」問題はまず文字だけの式を、必ず書いてください。
（理由は後で言います）

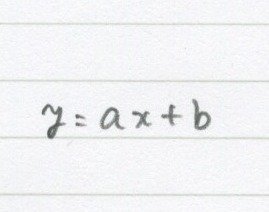
そしたら次はどうしようか。

前のページで書いたけど、
ｙ＝ａｘ＋ｂで大切な文字はなんだったっけ。

それは「ａ」と「ｂ」です。
この「ａ」と「ｂ」が直線の形を決めるんだったよね。

だからｙ＝ａｘ＋ｂって見たら
ｙ＝ａｘ＋ｂって強調されて見えるくらいにしといてください。

だからさっきの問題文で、
大切なのは「傾きが２」という情報です。
次にそれだけを書きます。

ａは分かったけど、ｂがまだ分かりません。

ここで「点（１，－１）」について考えます。
これも前のページでやったけど、これは（ｘ，ｙ）の座標のことだよね。

だから、（１，－１）をｘとｙに代入しちゃいます。

あとは計算です。ｂが知りたいので「ｂ＝」にします。

これでｂが出ました。
ここまででａもｂもわかったので、最終的な答えは

こうなります。これで答え！

ーーーーーー

【計算ミスの減らし方】

ただ、なんか長くてめんどくさそうと思った人。

そのせいで大体の人が、
最初から一気に「ｘもｙもａも」代入します。
ｙ＝ａｘ＋ｂも書かないし。

どうなるかやってみるね。

いや答え出るんじゃん！
そう思うかもしれない。でもね。

　① 代入の段階で計算ミスが起こりやすい
　　（「ｙ＝ａｘ＋ｂ」って書いておけば、見ながら代入できた）
　　
　② ｂが出たあと、答えを頭の中で作るからミスしやすい
　　（「ｙ＝２ｘ＋ｂ」を書いておけば、そこに代入できた）

など危ない理由として挙げられます。

このサイトのいろんなところに書いてあること。
「見た目でやられたらダメだよ」ということが、
数学では一番と言っていいほど大事です。

　見た目でやられて
　→　考えることを放棄する

　見た目でやられて
　→　その場だけの一番楽な方法を選ぶ

苦手な人のほとんどがこれです。
でも思い出してほしいの。

・解き方を忘れてめんどくさかったこと
・一次関数ってそもそも何だか忘れてめんどくさかったこと
・計算ミスのせいで点が低くなったこと
・計算ミスのせいでやり直しをさせられたこと

このほうがずっとめんどくさくないか！！！！ってことを、です。
そもそも、混乱したからこのサイトにたどり着いたわけだよね。
適当にやったら、混乱は継続だ。
せっかくなら、どうせなら、できるようにしようよ。

じゃあ、数学で間違えないために大事なことを教えておくね。

【数学で間違えないために大事なこと】

・ミスをしないためのやりかたを解き方に組み込んでおくこと
・１行に１つのことしかしないこと

これが、とても大事なことです。

みんな「計算ミス（ケアレスミス）しなければもっと取れた」とか言うし、
先生も「次は計算ミスに気をつけろよ」って言うでしょ。
でもどうやって？

ケアレスミスは、ケア（注意）がレス（ない）ことによるミスです。
じゃあこれから、永遠に集中しておくことは可能？
言うのは簡単だけど、ケアレスミスをケアするって、どうやるのよ。

だから「仮に集中してなくても」解けるようなやり方を、
「解き方の中に組み込んでおく」こと。
そして「常に」それでやっておくことが大事です。
常にやっておけば、慣れてしまうから、面倒に感じることもないです。

これは工事現場や作業場でも使われてる考え方（なはず）です。
集中してない、を理由に大事故になったら、とっても大変からです。
電車の指差し確認だって、毎回やってるから面倒ではないはずだよ。

その組み込むやり方のひとつが「１行に１つのこと」です。
さっきの長く見えた答えだって

　①　ｙ＝ａｘ＋ｂって書いた
　②　大事なａを先に代入した
　③　ｘ、ｙに点を代入した
　④　計算したらｂが出たので答え

ってやってるだけ。
１行に１つのことしかしなければ、頭の中はスッキリして計算できます。
つまりミスが少ない。

面倒臭がって、一度に全部代入して１行でいろんなことやると、
頭の中がいっぱいになる。
いっぱいだから意外と時間もかかる。ミスも増える。
どっちが面倒か、もう気付こうね。

だとしても「① ｙ＝ａｘ＋ｂって書く」は、いらない気がする！
そう思う人もいるかも。
でも中学で扱う関数は比例、反比例、一次関数、二次関数です。
高校だともっと増える。
今だけじゃなくて、試験のときも絶対に覚えてられる？

毎回書くクセをつければ、
一次関数＝直線＝ｙ＝ａｘ＋ｂっていう感覚はきっと忘れないし、
ｙ＝ａｘ＋ｂって書いたのを見ながら代入するから頭の中はスッキリです。
だから、毎回解き方に組みこんでおく。

何が面倒かを、よく考えてね。
数学なんてずっと同じことのくりかえしだ。
できないほうが、このあともずっとめんどくさい。

長い＝めんどくさい、はもうおしまいです。

ーーーーーー

【一次関数の式の決定（ｂを代入）】

それじゃあ続いての問題です。

さっきと似てるような似てないような問題文。
とりあえず「ｙ＝ａｘ＋ｂ」です。

そしたら、
問題文の中で大切なのは切片のｂだよね。先に代入。

そしたら、点を代入。

「ａ２」じゃなくて「２ａ」ね。
「ａ×２」という意味だからね。

あとは計算。

はい余裕。
ってかさっきと同じ式だったね。

ーーーーーー

【一次関数の式の決定（通る２点を代入）】

じゃあ最後の問題です。

あれ！ａもｂもない！
点だから、ｘとｙだけです。
でも、さっきと違って、どうやら「２点」通ってるっぽいね。

このパターンの問題は

こんなふうに書き換えられても同じ意味です。

でもまずはいつもと同じ。
ｙ＝ａｘ＋ｂって書きます。

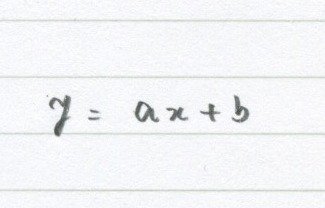
ａとｂがないんだから仕方ないよね。
（−１、５）（３、３）をそれぞれ、ｙ＝ａｘ＋ｂに代入します。

なんとなく予想つくかな。
これは連立方程式です。

（苦手な人は下のページだけやってきて！！！）

解きます。

ａとｂの連立方程式が出てきたと思えば、こんなふうに答えられます。
最後の答えが「ａ＝２、ｂ＝－３」じゃないことに注意ね！！

これは一次関数の問題だったんだから、
「ｙ＝ａｘ＋ｂ」の形で答えです。

２点求まってるときはこんな解き方。連立でした。

（というか、直線は２点が分かれば定規で引けるので、２点が分かれば直線を求められる、ということです。後々出てくるよ。ちょっと難しいけどね）

ーーーーーー

意外と難しくなかったでしょ。
ただ途中で注意したけど、
ショートカットしすぎないようにだけは注意してください。

［練習問題］（答えは下）

（あ、「変化の割合＝直線の傾き」だからね！）

［全ページに飛べるもくじ］

［次のページ］一次関数の理解が深まる面積問題 【長さの求め方】

［答え］