変化の割合 【二次関数 ｙ＝ａｘ²】

［前の前のページ］二次関数（式→グラフ）

［前の前のページ］二次関数（ｙ＝ａｘ²の決定、グラフ→式）

二次関数の基本は上の２つでおしまいです。
意外と少ないよね。分からないときは膨大に思えてしまうものです。

そして今回は変化の割合。
変化の割合ってなんなんだっていう説明は後でします。
とりあえず求められるようにしちゃうよ！

ーーーーーー

【変化の割合】

一次関数でこういう説明があったの、覚えてるかな。

「ａ」の説明を読んでね。

一次関数の「ａ」は、

「直線の傾き」で、
「変化の割合」で、
「ｘの増加量 分の ｙの増加量」でした。

たとえば一次関数「ｙ＝－３ｘ＋６」の変化の割合は、
傾きａを答えるだけ。答えは「－３」でした。

だけどａが変化の割合なのは一次関数だけです。
二次関数の「ｙ＝ａｘ²」のａには、まったく関係ない。

ただ上の説明で、いつも使えるのもあります。

ここ！

「変化の割合」は「ｘの増加量 分の ｙの増加量」です。
この式は二次関数でもどこでも使えます。
（一次関数がたまたま、この式とａが同じだっただけ）

上と下の、どっちがｘでどっちがｙかは、
一次関数のグラフの描き方が頭に入ってれば覚えられます。

「横に２、縦に３」とか、
「２行って、３上がる」とかやったもんね。そのままです。

とにかくこの「変化の割合」＝「ｘの増加量 分の ｙの増加量」
これは覚えるしかない。
暗記といったら、連呼（れんこ）だったね。
声に出して読みまくる。これしかないです。

変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量、変化の割合 ＝ ｘの増加量 分の ｙの増加量・・

何回も読んだら覚えないほうが難しい。
覚えたら次行きましょ。

ーーーーーー

【そもそも増加量って？】

もうひとつだけ知識つけておきます。
「増加量」についてです。

この式の「増加量」って、分かる？

「増加量」っていうのは
「どこからどこまで増えたか」っていうこと。
去年の150cmの身長が、今年157cmになってたら、
どのくらい増えてる？ってこと（増加量は7cm）

この「どこからどこまで」という考え方は
「長さ」とか「距離」とかと一緒です。

150cmから157cmは暗算でできるけど、
じゃあａからｂならどうする‥？

そういう解説を一次関数の面積問題のページで入れてました。
簡単に載せるね。

この「さいご－さいしょ」は、
「長さ」でも「キョリ」でも「増加量」でも使えるよ、
ということです。

さあ。これで問題に行けるよ。

ーーーーーー

【変化の割合の問題】

さあ！
とりあえず実践しながら変化の割合を身につけようね。

こんな問題。

とりあえず「変化の割合」の問題なんで、こうします。

変化の割合って「ａ」とか「ｂ」みたいな文字がないんだ。
だから言葉をこうやって（　）で囲んで書いとけばいいです。
（たぶん）

そしたらこの式

だったね。

問題文の「ｘの値が１から４まで増加」を使って、
「増加量」を出します。

「１から」「４まで」だから
さいしょが「１」さいごが「４」です。
だから「さいご－さいしょ」は「４－１」です。

計算しないで書いてください。

分数の上も、増加量（さいご－さいしょ）だよね。
だから「－」だけ先に書いてください。

ここからがポイント。

そういえば問題文の「ｙ＝２ｘ²」を使ってないよね。
そんなことはあり得ないはず。
ここで使います。

手書きで説明するね。

こういうふうに、
下に書いた「さいご－さいしょ」を、
それぞれ「ｙ＝２ｘ²」に代入して、同じように書いてください。

ｘ＝４を代入してｙ＝２×４²で「ｙ＝３２」。
ｘ＝１を代入してｙ＝２×１²で「ｙ＝２」。

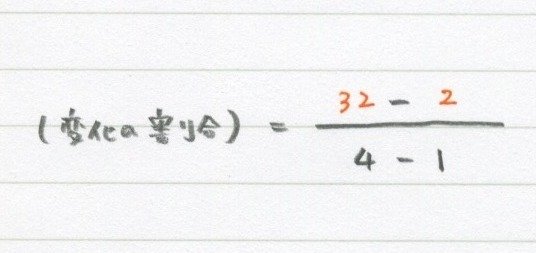
こういうふうに代入します。
だから計算しないで「４－１」って書いといたんだね。

じゃあ後は計算！

こうです。
単位はなくていいです。

ーーーーーー

【変化の割合の問題②】

練習でもう１問やってみます。

似てる問題だね。
まずはこう書きます。

最初に「－」は、上下どちらにも書き込んどいてください。
（さっきは初めての説明だから省いたの）

そしたら問題文の「ｘの値が－３から－２まで」。
－３が「さいしょ」、－２が「さいご」です。
「さいご－さいしょ」だったよね。書き込みます。

マイナスなので（　）して書き込んでください。
このマイナスがゴチャゴチャの原因なんだ。
だからさっき、最初に「－」って書いといたのでした。

そしたら次は分子（ｙの増加量）だね。
それぞれ「ｙ＝２ｘ²」に代入します。

ｘ＝－２を代入してｙ＝２×（－２）²で「ｙ＝８」。
ｘ＝－３を代入してｙ＝２×（－３）²で「ｙ＝１８」。

これを書き込みます。

じゃあ計算です。

これで答えね！

ーーーーーー

【ｘの増加量とｙの増加量の出し方】

ちなみに今の答えの、約分する前のこの部分。

ここで、「ｘの増加量」と「ｙの増加量」が分かります。

だから「ｘの増加量」「ｙの増加量」「変化の割合」を
「ぜんぶ求めろ」って言われたら、
変化の割合だけ求めれば、なんとかなるからね。

ーーーーーー

【変化の割合（ａの値）】

次。

難しそう？
見た目だけでやられちゃだめだからね。
このサイトで突然できない問題は出さないからね。

見た目が難しそうな問題に出くわしたら。
やることは２つだけ。

　①　ていねいに読む
　②　とにかく手を動かす

見た目が難しいとだいたい、
「えー難しそうと飛ばして読む」「手が動かない」
になりがちです。
だから上の２つは、当たり前だけどとっても大事。

ていねいに読んで、
とにかくできるところから手を動かすのみ！

　「ｙ＝ａｘ²」で
　「ｘの値が２から４まで」の変化の割合

これって、文字「ａ」が入ってる以外は、さっきと同じだ。
じゃあ、とりあえずやってみようよ！

ここから

こうだね。
（ｙ＝ａｘ²に「ｘ＝４」と「ｘ＝２」を代入してます）

とりあえず解きましょう。

はい解きました！ここまでは出来たね。

変化の割合に、なぜか文字ａが入ってる。
そしたら問題文の

　変化の割合が－３

を使おうよ。

ね。
そしたら「６ａ＝－３」っていう方程式が出てきたでしょ。
じゃあ解くだけ。

これで答えです。
（方程式が分からなかったら必ずここをやること）

見た目が難しそうでも、

　①　ていねいに読む
　②　とにかく手を動かす

これだけで、意外となんとかなったね。

ーーーーーー

【変化の割合の説明】

ていうか変化の割合ってなんだ！
軽く説明します（飛ばしてもいいです）

「変化の割合」って
「どのくらい変化するの？」ってことなの。

ちょっと比べてみます。

これと

これ。

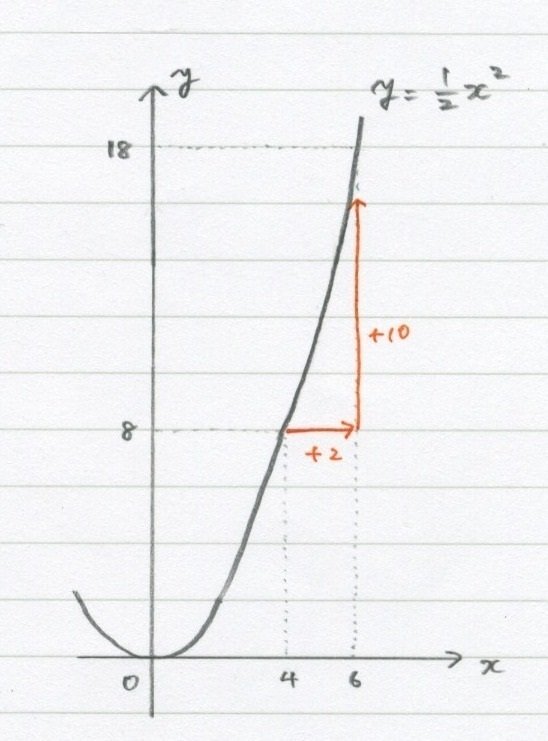
どちらもｘ（横方向）に「２」増えています。
（「２から４」と「４から６」）

どっちも横に「２」増えてんのに、
１枚目の方は「上に６」で、
２枚目の方は「上に１０」。

実際に変化の割合出してみようね。
ｘが「２から４」は、

ｘが「４から６」は、

こうなります。さっきより大きい。

「２から４」より「４から６」の方が
「増える力がありますよ」っていうのが、
変化の割合を出すと分かるんだね。

（曲線だから、
　場所によって「変化する力」が違うということです）

こういうジェットコースターがあるとして、

降り始めのところと、
降りてるところは、
「変化の割合」全然違うよね！ってこと。

［降り始め］

［降りてる途中］

同じだけ横に進んでるのに、降りてる量が全然違う。

同じ条件で、
「どのくらい変化するのかの違い」を出せるのが
変化の割合だったんです（簡単に言うとね！）

こういうときはもちろんマイナスになるからね。
（ｙ（縦）の増加量がマイナスだから）

ーーーーーー

【余談】

二次関数の変化の割合は
「ａ（ｘ₂－ｘ₁）」
って教わった人もいるかもしれない。

公式があるほうが、さっきまでのより簡単そうだよね。

でもどうして教えなかったのか。
よかったら考えてみてください。
もくじにある「本当の楽ってなに」のページがヒントです。

変化の割合の式に、
さいしょを「ｘ₁」さいごを「ｘ₂」として、
ｙ＝ａｘ²を使って入れてみたら、気付けるかもしれません。

ーーーーーー

ということで変化の割合はここまで。
なんとなく難しそうだったけど、でもなんとかなったね！

練習問題、やっつけといてね。
２問だけだけど、よーく考えてクリアしてください。
そんで何回か解けばもう大丈夫です。

［練習問題］答えは下

［全ページに飛べるもくじ］

［次のページ］２次関数（変域）

［答え］